Word Representation

What is NLP?

Natural language processing (NLP) refers to the field of enabling computers to process natural language or generate natural language.

Such NLP technologies play a critical role in communication tools between humans and machines, such as smart speakers. Additionally, they are utilized in human-to-human communicaition for functions like automated translation and find applications in various fields, including document summaraization and sentiment analysis.

While there are various tasks in NLP, this discussion will begin by addressing the foundation concept of word representation.

Word Representation

Let us first introduce the fundamental concepts. Semantics refers to the study of how meaning is conveyed through symbols and language. Computational semantics, on the other hand, involves the study of methods to automate the construction and inference of meaning representations in natural language.

Why is computational semantics necessary?

To understand this, consider one of the simplese NLP examples: sentence classification.

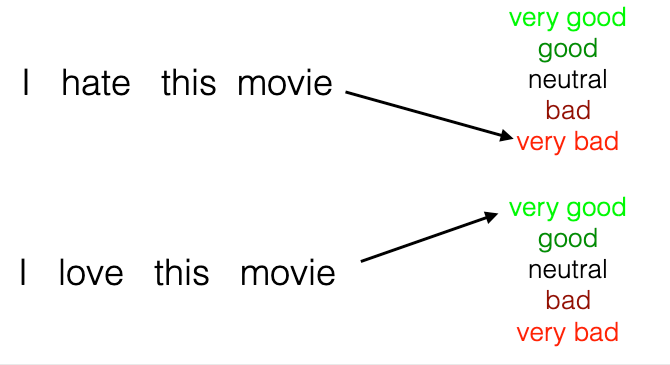
Let us consider a simple classification logic: the Bag of Words (BoW) approach. This method quantifies text data by focusing solely on the frequency of word occurrences, completely disregarding the order of the words. Using this approach, the following results can be obtained.

However, such a simplistic rule is likely to produce poor results in cases like the following example.

The word “film” is a neutral term, but the model does not recognize this. Furthermore, how the model handles an unfamiliar word like “worderful” remains unclear. For these reasons, even in basic NLP tasks, a certain degree of word-semantic learning is necessary.

Word Semantics

There are two primary approaches to representing the meaning of words: lexical semantics and distributional semantics. Lexical semantics focuses on how the meanings of words are interconnected, often relying on resources such as dictionaries, thesauri, ontologies. However, lexical semantics has several limitations: it struggles to account for nuances, faces challenges in incorporating new words, and is often influenced by subjective perspectives.

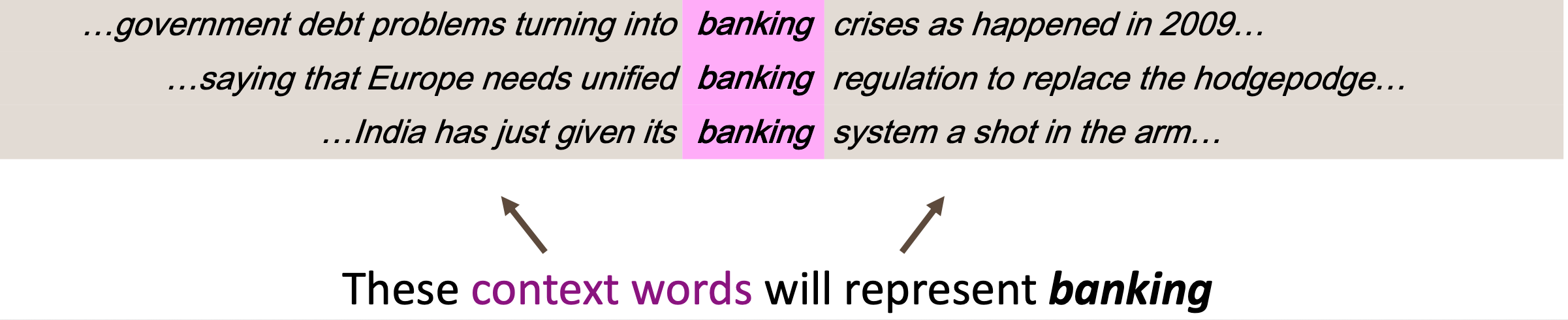
Distributional semantics is based on the distributional hypothesis, which posits that words with similar meanings tend to be used in similar contexts. Instead of defining synonyms individually, it derives the representation of a word $w$ (e.g. banking) from the multitude of contexts in which the word $w$ is used.

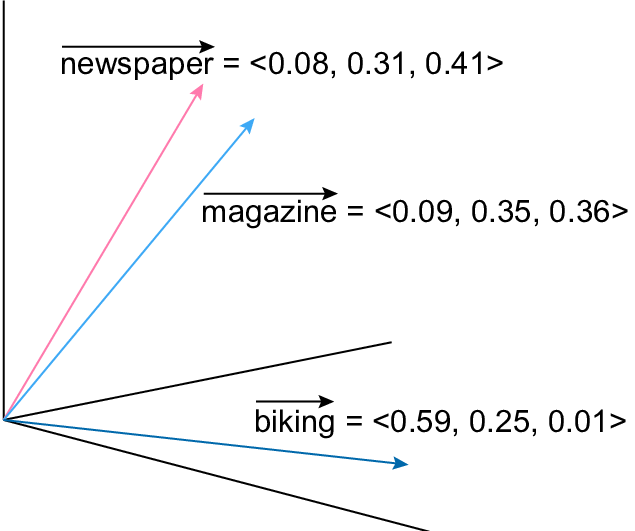
For computational semantics, words must be represented as vectors. The key idea behind these word vectors is that words with similar meanings point in similar directions in the vector space. Consequently, the similarity between words can be measured using theire dot product or cosine similarity.

Representing a Word as a Vector

Methods to Represent Words as Vectors

There are several methods to represent words as vectors. One straightforward approach is to use a one-hot vector, where each dimension corresponds to a unique word.

However, this approach is highly inefficient and suffers from the problem that all words are treated as orthogonal to one another. For example, it is problematic that the dot product between “movie” and “film” equals 0, as they are semantically similar.

Subsequent methods leveraged distributional semantics, such as TF-IDF and PMI, which utilize word co-occurrence relationships within documents or sentences. However, these counting-based methods are inherently constrained by the curse of dimensionality.

This limitation was addressed by a groundbreaking paradigm developed by Google in 2013: Word2Vec.

Word2Vec

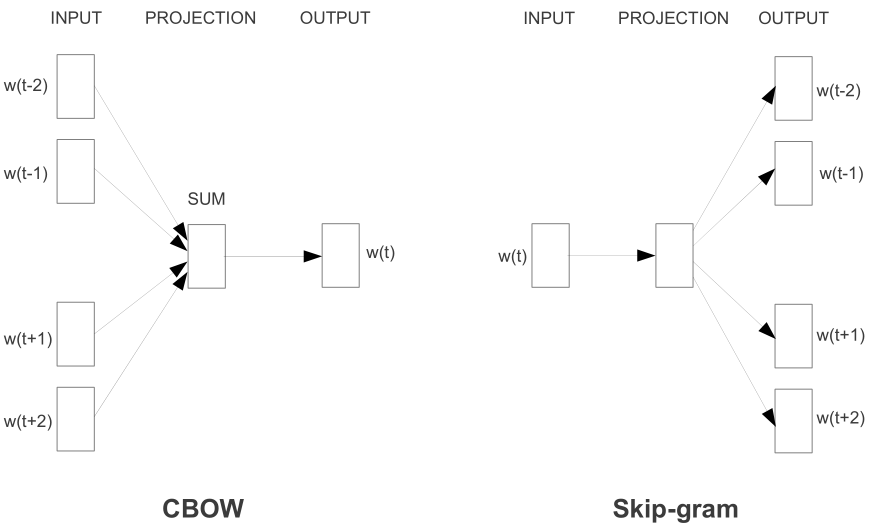
Word2Vec operates based on the following two training architectures:

1. CBOW (Continuous Bag of Words)
   • Predicts the target word (center word) based on its surrounding context words.
   • Input: Target words
   • Output: Context word
   • Example: In the sentence “I am learning Word2Vec,” CBOW uses “I,” “am,” and “learning” as input to predict “Word2Vec.”
   • Typically faster and performs well on smaller datasets.
2. Skip-gram
   • Predicts the surrounding context words based on the target (center) word.
   • Input: Context words
   • Output: Target (center) word
   • Example: In the sentence “I am learning Word2Vec,” Skip-gram uses “Word2Vec” as input and predicts “I,” “am,” and “learning” as outputs.
   • Tends to perform better on larger datasets.

CBOW has similar ideas used in BERT: masked language model (Self-supervised, distributional hypothesis …).

Skip-gram

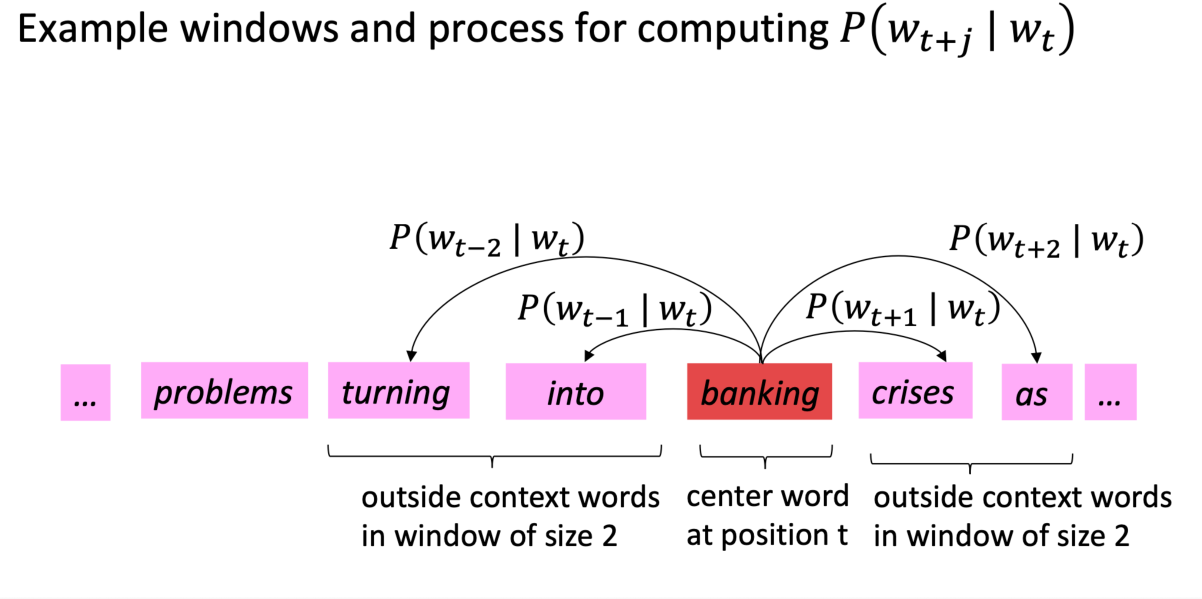
Here, let us delve deeper into the skip-gram model. The purpose of the model is to compute $P(o \vert c)$, the propability of a context words $o$ given a center word $c$, using the similarity between their word vectors, and to maximize this probability.

In other words, the objective of the skip-gram model is to maximize the probability of any context word given the centor word, which can be expressed as follows:

\[\max L = \frac{1}{T} \prod_{t=1}^T \prod_{-m \leq j \leq m, \, j \neq 0} P(w_{t+j} \mid w_t; \theta)\]

where $m$ is the size of the window.

By applying the negative logarithm, the problem can be reformulated as a minimization problem:

\[- \log L= -\frac{1}{T} \sum_{t=1}^T \sum_{-m \leq j \leq m, \, j \neq 0} \log P(w_{t+j} \mid w_t; \theta)\]

In this case, $P(o \vert c)$ is calculated using the softmax of the dot product (similarity) between the outside word vector and the center word vector:

\[P(w_{t+j} \mid w_t) = P(o \mid c) = \frac{\exp(u_o^T v_c)}{\sum_{i=1}^V \exp(u_i^T v_c)}\]

One significant issue is that normalization over the entire vocabulary $\vert V \vert$ is computationaly too expensive and surely not feasible.

To address this, two alternative (and feasible) solutions have been proposed: hierarchical softmax and negative sampling. These methods will be discussed in the next.