Variational Autoencoders (VAE)
Generative model 이란 training data $p_{data}(x)$으로부터 유사한 분포를 갖는 새로운 sample ($p_{model}(x)$)을 생성하는 모델을 말한다. Explicit modeling은 그러한 $p_{model}(x)$을 수리적으로 정의하고 이를 표현한 모델을 말하며, implicit modeling은 $p_{model}(x)$을 따로 정의하지 않고 생성해내는 모델을 말한다.
Variational Autoencoders (VAE)
- 참고: Autoencoder
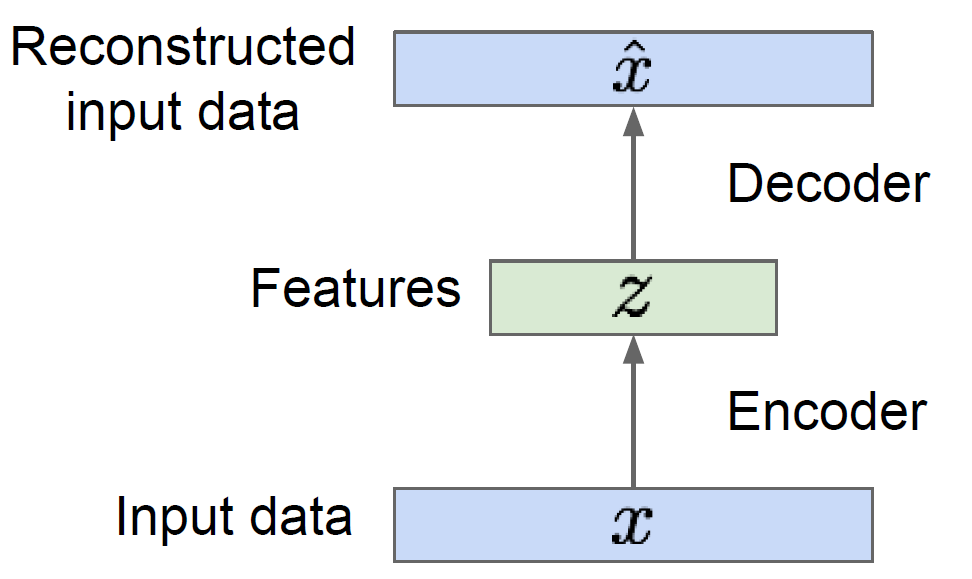
Autoencoder (AE)를 다시 생각해보자. 이는 주어진 input data $x$를 다시 생성해내는 모델을 말한다. 이 때, decoder 부분만을 생각해본다면, 결국 reconstructed input data $\hat{x}$는 feature 또는 latent $z$로부터 생성되는 값이다.
Variational autoencoders (VAE)의 아이디어는 ‘이 latent $z$가 특정 분포를 따르도록 학습을 시킨다면, 그 분포로부터 sampling한 값을 이용해서 새로운 data를 생성해낼 수 있지 않을까?’ 이다.
즉, VAE는 explicit modeling의 일종이다.
Probabilistic Modeling of VAE
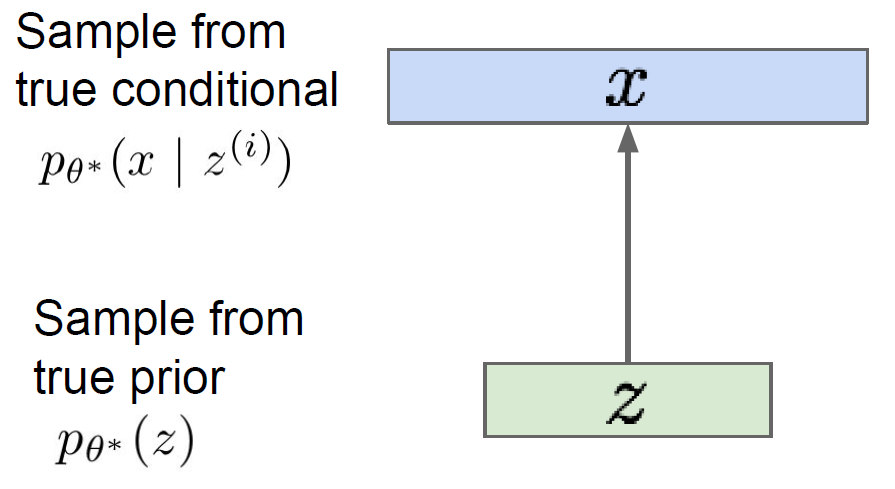
Image를 생성하려는 문제를 생각해보자. 이 경우, $x$는 image가 되고, $z$는 $x$를 생성하기 위해 사용되는 latent가 된다. 그리고 해당 문제의 목적은 $x$에 대한 likelihood를 maximize하는 parameter $\theta^\ast$를 찾아내는 것이 된다.
위 모델에서 우리가 control하려는 변수는 latent $z$이다. 따라서, prior $p_\theta(z)$는 Gaussian과 같이 단순하게 설정하고, $p_\theta(x \mid z)$는 neural network와 같이 복잡한 모델로써 표현하여 전체 모델의 complexity를 조절한다.
만약 MLE $\theta^\ast$를 찾은 경우, 우리는 다음 식을 이용해 image를 생성해 낼 수 있다.
\[p_\theta(x) = \int p_\theta(x \mid z) p_\theta(z) dz\]하지만, 위 식의 어려운 점은 $\int$ 에 대한 계산이 쉽지 않다는 것이다. 만약 $z$가 finite-dimensional vector이고 $p_\theta(x \mid z)$가 Gaussian distribution인 경우, $p_\theta(x)$는 mixture of Gaussian distribution이 된다. 허나, 이러한 단순한 가정은 image 생성과 같은 복잡한 작업에서는 좋은 성능을 기대하기 어렵기에, 다른 접근이 필요하다.
또 다른 접근으로 posterior $p_\theta(z \mid x)$를 이용할 수 있다.
\[p_\theta(z \mid x) = p_\theta(x \mid z) p_\theta(z) / p_\theta(x)\]이 방식의 어려운 점은 $p_\theta(z \mid x)$에 대한 계산이 쉽지 않다는 점이다. 따라서 VAE에서는 posterior를 근사하는 새로운 함수 $q_\phi$를 통해 이를 계산한다.
\[q_\phi(z\mid x) \approx p_\theta(z \mid x)\]이를 종합하면, 결국 VAE는 conditional likelihood distribution $p_\theta(x \mid z)$를 decoder로, approximated posterior distribution $q_\phi(z\mid x)$를 encoder로 계산하는 AE 모델이 된다.
우리가 알지 못하는 분포를 근사시켜 임의의 값을 생성해내는 VAE는 variational inference에서 이름과 개념을 가져왔다.
ELBO
Deep learning을 이용한 학습을 위해서는 differentiable loss function을 적절하게 설정하는 것이 필요하다. VAE는 이를 위해 ELBO 를 사용한다.
\[L_{\theta, \phi}(x) := \mathbb{E}_{z \sim q_{\phi}(\cdot \mid x)} \left[ \ln \frac{p_{\theta}(x, z)}{q_{\phi}(z \mid x)} \right] = \ln p_{\theta}(x) - D_{KL}(q_{\phi}(\cdot \mid x) \| p_{\theta}(\cdot \mid x))\]위 식은 아래와 같이 다시 쓸 수 있다.
\[L_{\theta, \phi}(x) = \mathbb{E}_{z \sim q_{\phi}(\cdot \mid x)} [\ln p_{\theta}(x \mid z)] - D_{KL}(q_{\phi}(z \mid x) \| p_{\theta}(z))\]즉, ELBO를 증가시키는 것은 $\ln p_{\theta}(x)$를 증가시키고, $D_{KL}(q_{\phi}(z \mid x) | p_{\theta}(z \mid x))$를 감소시키는 것과 동일하므로, ELBO를 maximizing함으로써 적절한 학습이 가능하다.
\[\theta^*, \phi^* = \arg\max_{\theta, \phi} L_{\theta, \phi}(x)\]일반적으로, 적절한 학습 및 loss function 설정을 위해 $p_\theta(x\mid z), p_\theta(z), q_\phi(z \mid x)$가 모두 Gaussian을 따른다고 가정한다.
Encoder and Decoder Networks
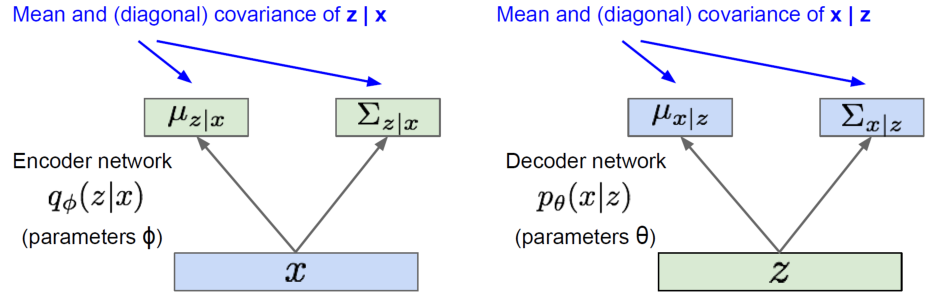
VAE에서 encoder와 decoder networks는 AE에서는 다르게 latent 또는 output을 직접 생성하지 않고, 해당 vector들에 가정한 분포(여기서는 Gaussian)의 parameter를 추정한다. 즉, encoder network는 $z \mid x$ 의 평균과 분산을, decoder network는 $x \mid z$의 평균과 분산을 생성한다.
Encoder와 decoder network는 각각 recognition/inference network와 generation network라고도 불린다.
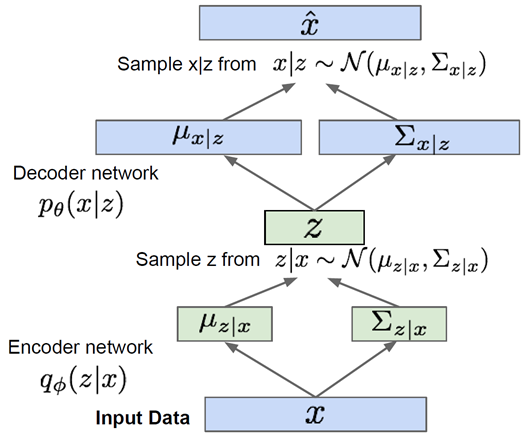
위 network를 연결하면 아래와 같으며, 해당 network의 최종 output $\hat{x}$이 우리가 생성해낸 image가 된다.
Generating Data with VAE
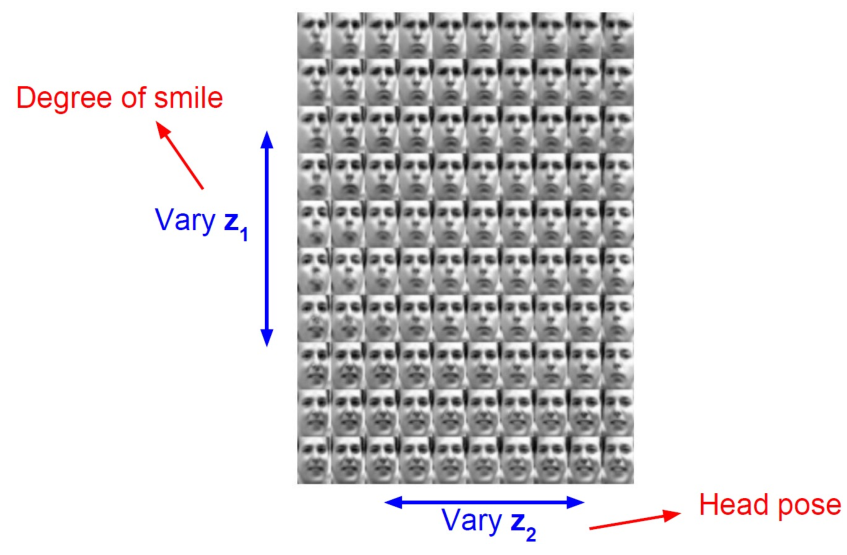
이렇게 학습된 VAE를 이용해서 새로운 image를 생성하기 위해서는 latent $z$의 값을 분포 내에서 조금씩 변형시켜주면 된다.
아래 그림과 같이 각 dimension의 값을 조금씩 변경시켜주면 상당히 자연스러운 image가 생성되는 것을 볼 수 있다.
특히, VAE와 AE를 비교해보면, AE의 경우 weighted average를 통해 값을 생성하므로 각 image를 투명하게 겹쳐놓은 것 처럼 image가 생성되나, VAE의 경우 두 image의 특징이 부드럽게 섞인 image를 생성하는 것을 볼 수 있다.
VAE는 blurry한 image를 주로 생성한다는 특징이 있다.