Unitary Image Transform

Unitary Transform

Unitary transform은 이미지 또는 신호의 데이터를 변환하는 linear transform으로 원래 데이터의 basis를 바꾸지만, 그 length는 보존한다.

Unitary transform은 복소수 공간에서 정의되는 변환으로, 실수 벡터 공간에서의 orthonormal matrix에 대응된다.

2D square image에서 다음과 같은 unitary transform이 있다고 하자.

\[H[u, v] = \sum_{x=0}^{N-1} \sum_{y=0}^{N-1} h[x, y] t(x, y, u, v)\]

• If separable and symmetric,

\[t(x, y, u, v) = t_1(x, u) t_1(y, v)\]

• In matrix form,

\[H = T h T^T\] \[h = T^{\ast T} h T^\ast \quad (\because T^{-1} = T^T)\]

Well-known Unitary Transforms

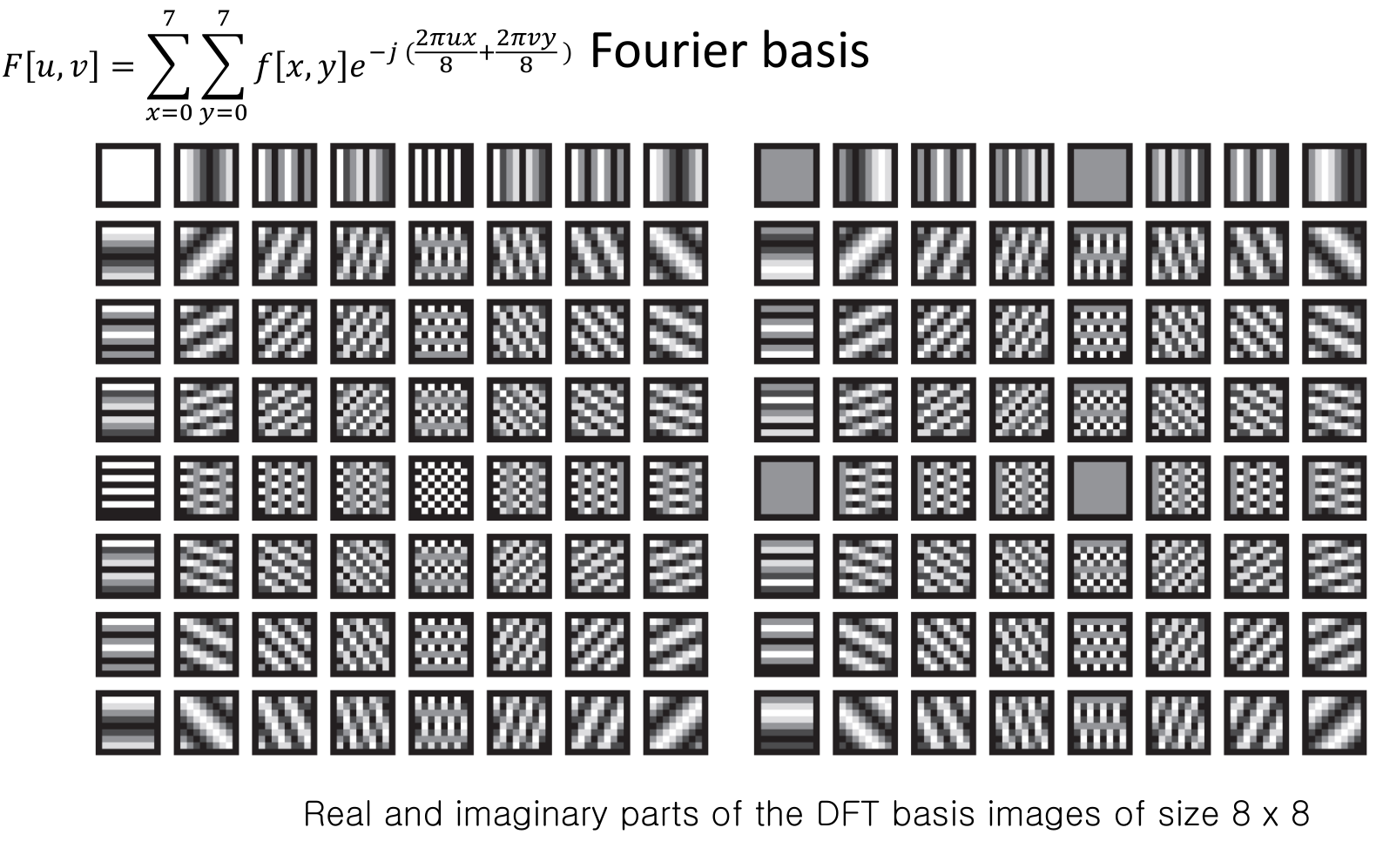
2D Discrete Fourier Transform

• 장점
  • Energy가 대개 low-frequency 계수에 몰려있다. (?)
  • Convolution이 곱 연산이 되기에 속도가 빠르다.
• 단점
  • Transform 결과 complex number가 생성됨
  • Basis function이 image와 같은 size
  • Edge를 구현하는 게 어렵다. (삼각함수이기에)

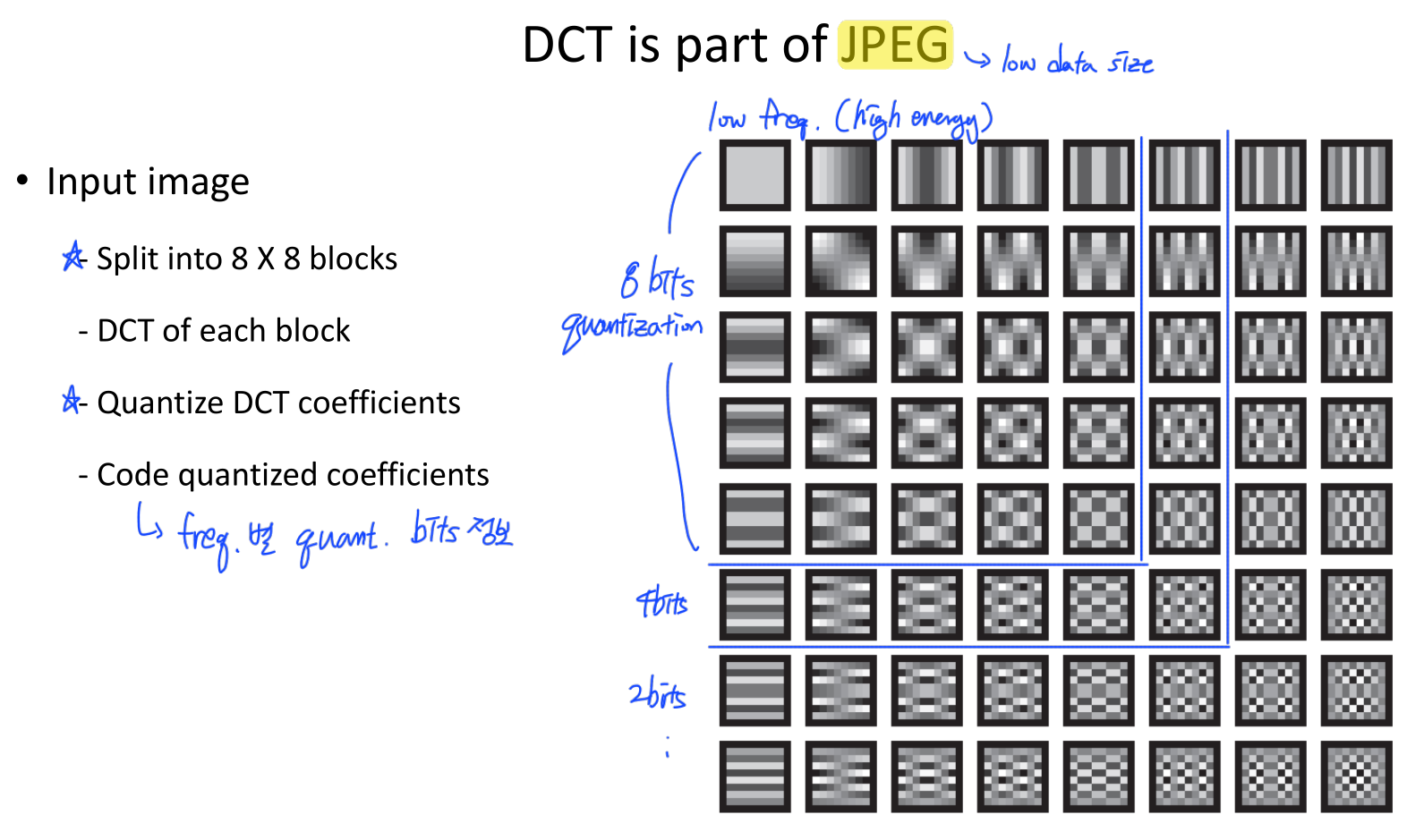
Discrete Cosine Transform

• JPEG 기술의 기본 토대이다.

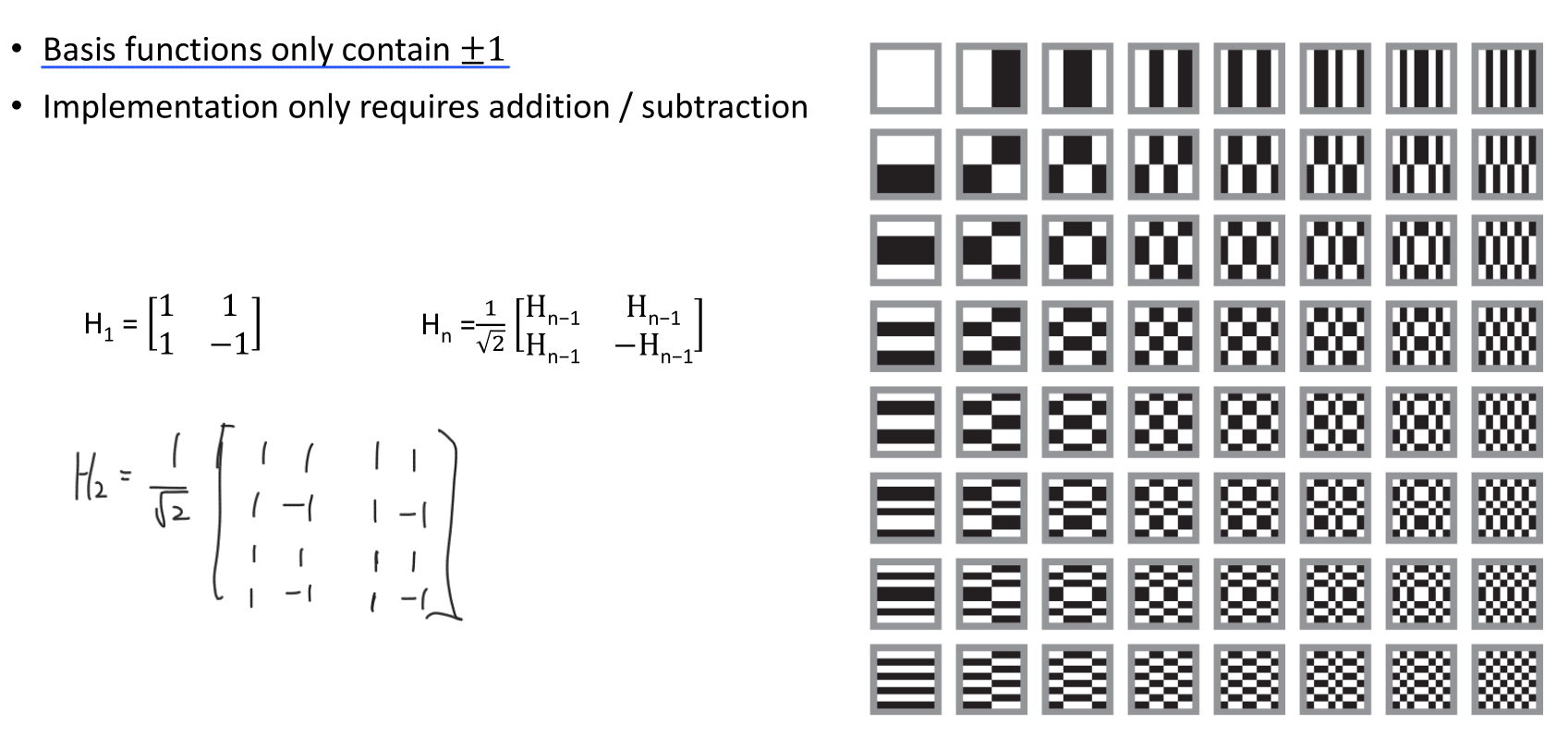
Walsh-Hadamard Transform

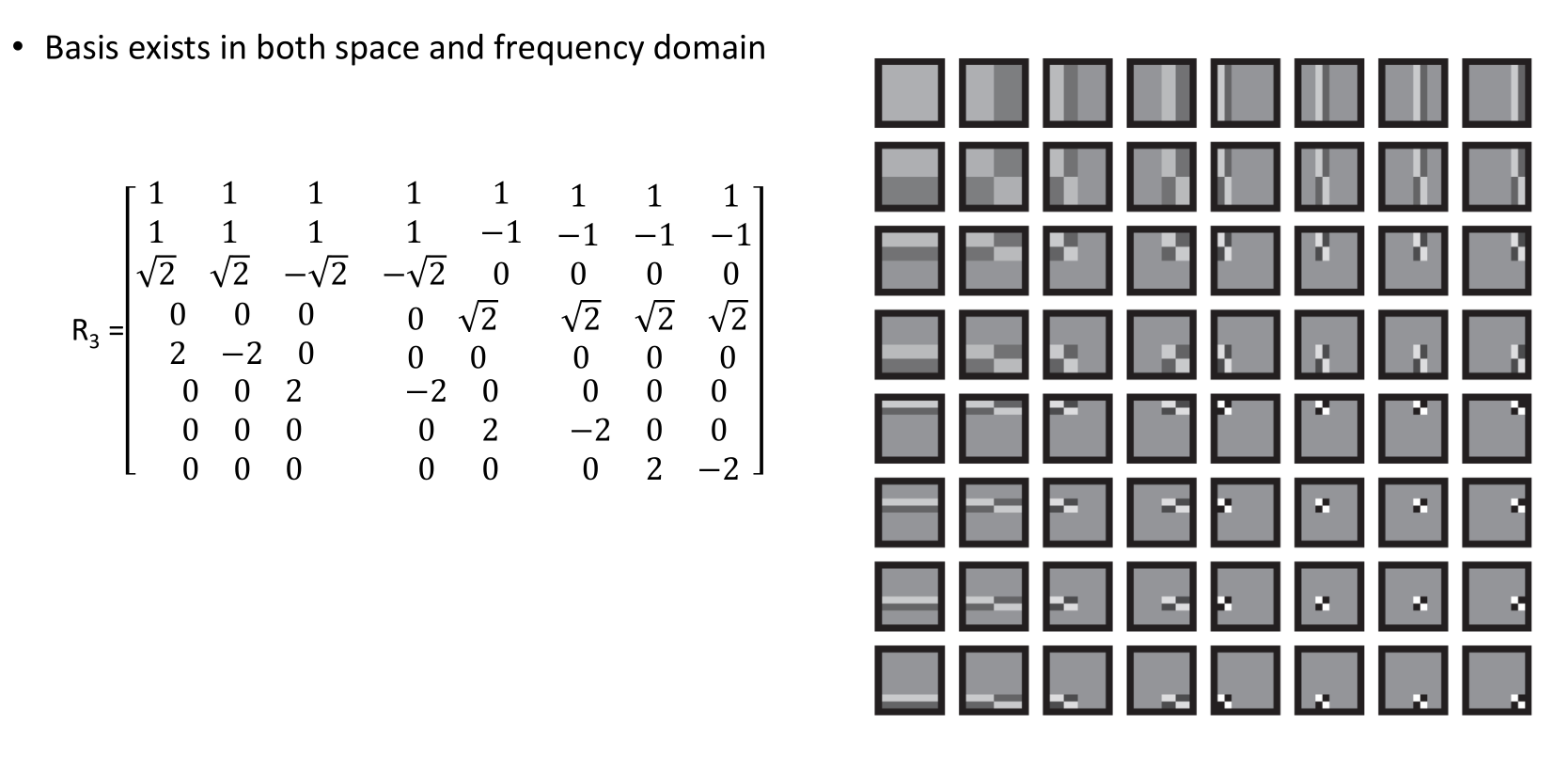
Haar Transform

• Wavelet transform의 simple version

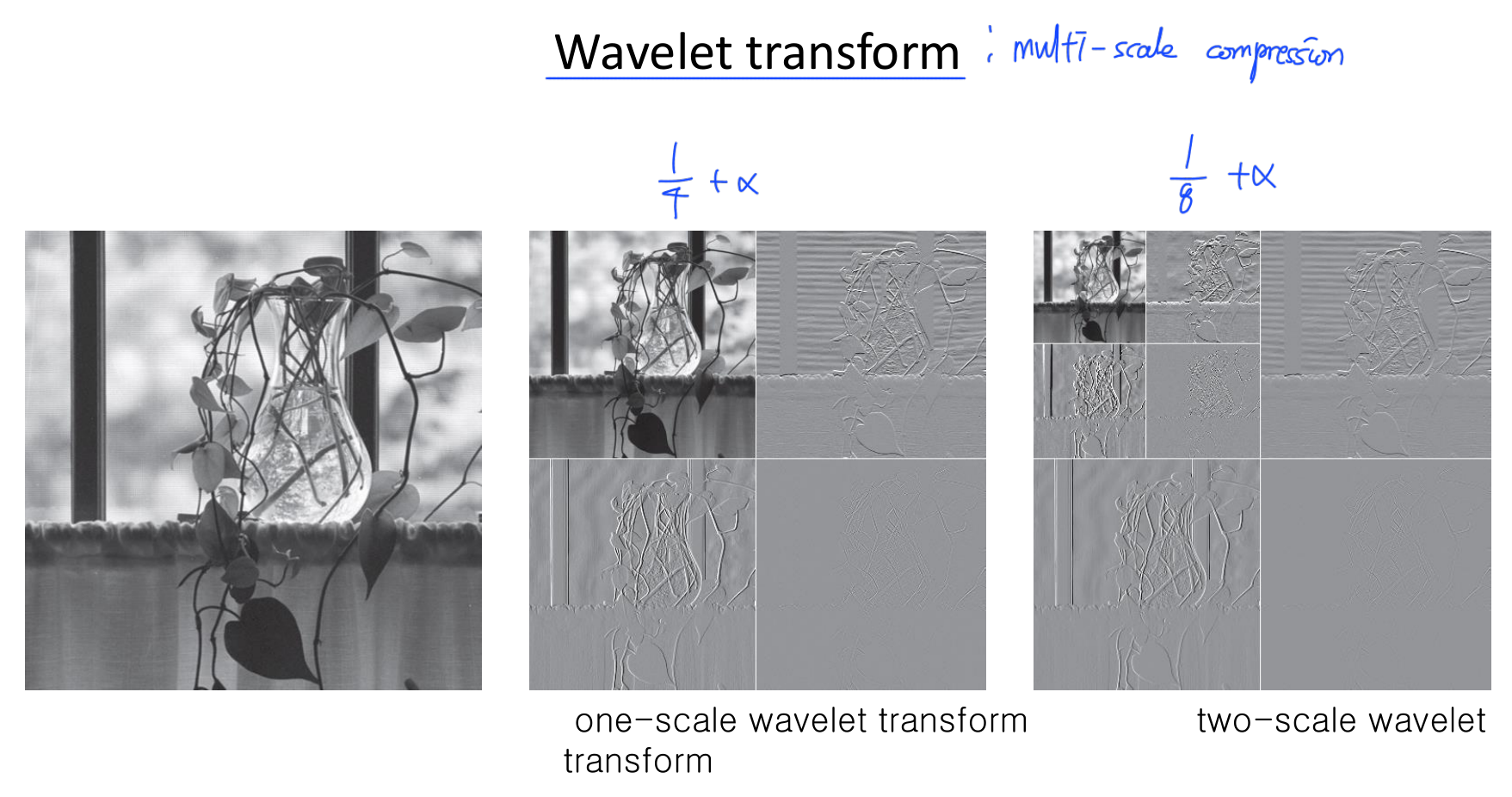
Wavelet Transform

• image 표현력이 좋음
• 계산이 빠름 ($O(N)$)
• 데이터 압축력 또한 좋음