Support Vector Machines

Support Vector Machines(SVMs)는 deep learning model의 큰 발전이 있기 전에는 boosting과 함께 가장 널리 사용되던 machine learning model이다.

Seperating Hyperplane

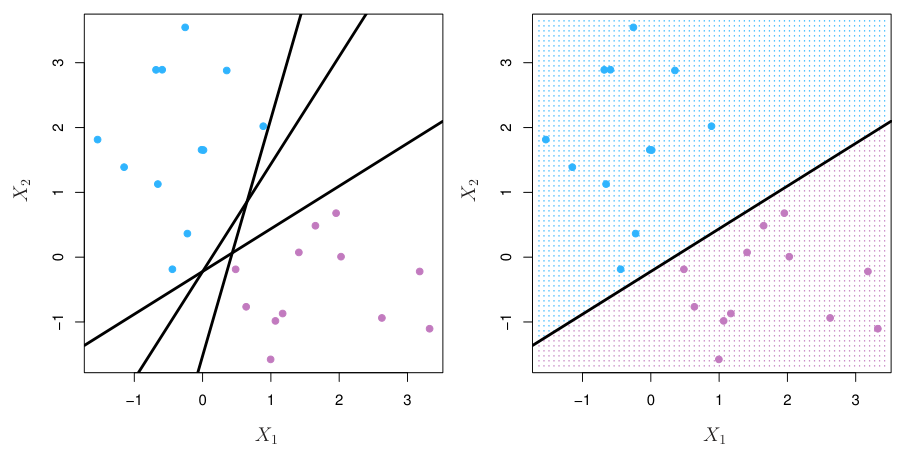
Classification 문제에 대해서, SVM은 기본적으로 class를 가장 잘 분리하는 plane, 즉 seperating hyperplane을 찾는 것을 목적으로 한다.

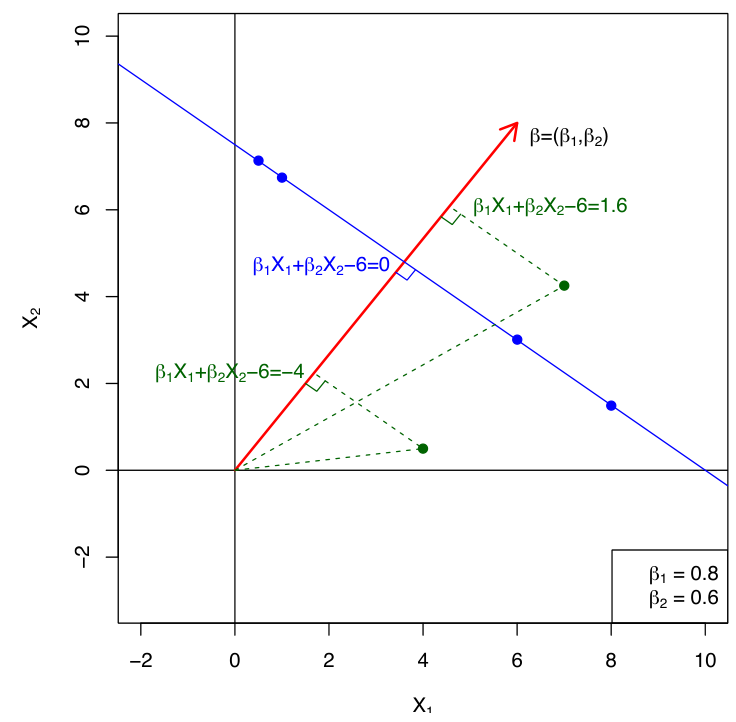
$p$-dimension space에서의 hyperplane이란, $p-1$ dimension을 가지는 flat affine subspace이다. 이는 다음과 같이 정의된다.

\[f(X) = \beta_0 + \beta_1X_1 + \beta_2X_2 + \dots + \beta_pX_p = 0\]

• 2-dim space의 hyperplane은 line이다.
• $\beta_0=0$이면 hyperplane은 origin을 지난다 (역도 성립).
• Vector $\beta = (\beta_1,\beta_2,\dots,\beta_p)$를 normal vector라고 부른다.
  • $\beta$ is orthogonal to the hyperplane.

어떤 Seperating hyperplane $f(X)$에 대해서, 각 class는 $f(X)>0$인 영역과 $f(X)<0$인 영역에 속하는지로 구분된다. 만약 blue 영역에서의 $Y_i$ 를 1, red 영역에서의 $Y_i$ 를 -1로 정한다면, 모든 $i$에 대해, $Y_i \cdot f(X_i) > 0$이 성립한다.

Maximal Margin Classifier

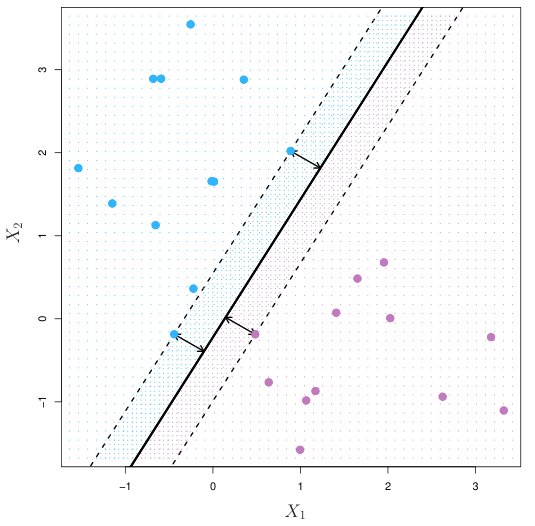
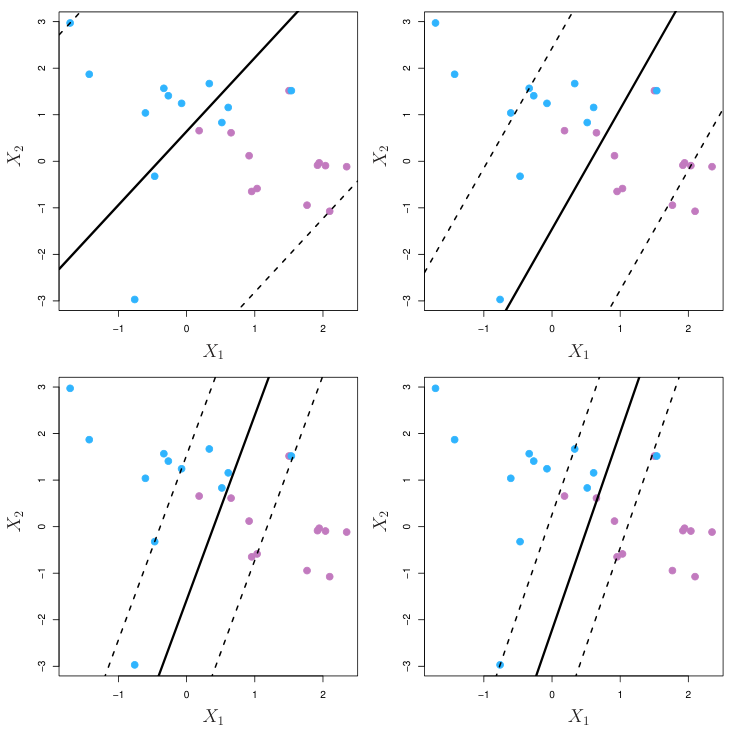
모든 가능한 seperating hyperplane $f(X)$ 중에서, maximal margin classifier는 두 class 사이의 gap 또는 margin을 maximize하는 seperating hyperplane을 말한다.

즉, 다음 optimization 문제의 solution이 된다.

\[\begin{aligned} & \text{maximize} & & M_{\beta_0, \beta_1, \ldots, \beta_p} \\ & \text{subject to} & & \sum_{j=1}^p \beta_j^2 = 1,\\ & & & y_i(\beta_0 + \beta_1 x_{i1} + \cdots + \beta_p x_{ip}) \geq M \quad \forall i = 1, \ldots, N \end{aligned}\]

이 문제는 Lagrangian dual을 사용하여 convex quadratic optimization 문제로 변환할 수 있다.

Margin 위 또는 안에 있는 data point 또는 vector들이 $\beta$를 결정하며, 이 vector들을 support vectors라고 한다.

Maximal margin classifier의 support vector들은 각 class 별로 hyperplane에서 가장 가까운 data point이다.

Support Vector Classifier

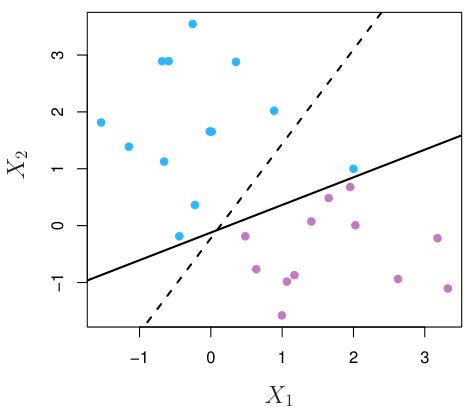
하지만 현실의 data는 당연하게도 분리되어 있지 않기 때문에, class들을 완벽하게 분리할 수 있는 seperating hyperplane은 존재하지 않는다.

혹여 일부 training data에 대해서 운좋게 class를 완벽하게 분리하는 seperating hyperplane을 찾더라도, outlier 또는 noisy data들로 인해 이는 오히려 overfitting을 유발할 가능성이 높다.

따라서, 어느 정도의 classification error를 감안하고서 적절한 hyperplane을 그리는 것이 더 좋은 성능을 보여주었으며, 이를 support vector classifier이라고 한다.

Support vector classifier는 다음 optimization 문제 (maximize soft margin)의 solution으로 얻을 수 있다.

\[\begin{aligned} & \text{maximize} & & M_{\beta_0, \beta_1, \ldots, \beta_p, \epsilon_1, \dots, \epsilon_n} \\ & \text{subject to} & & \sum_{j=1}^p \beta_j^2 = 1,\\ & & & y_i(\beta_0 + \beta_1 x_{i1} + \cdots + \beta_p x_{ip}) \geq M(1-\epsilon_i) \quad \forall i = 1, \ldots, N,\\ & & & \epsilon_i \geq 0 \quad \forall i = 1, \ldots, N,\\ & & & \sum_{i=1}^n \epsilon_i \leq C \end{aligned}\]

여기서 $\epsilon_i$는 각 data point가 misclassified 되었을 때의 error의 정도를 나타내며, C는 regularization을 결정하는 hyperparameter가 된다.

C값이 작을수록 error의 허용치가 작아지므로 더 flexible한 모델이 된다 (C=0이면 maximal margin classifier).

Support vector classifier의 support vector들은 margin 위 또는 안에 있는 data point들이다.

Hinge Loss

Hinge loss 함수는 다음과 같이 정의된다.

\[\ell_{\text{hinge}}(y, f(x)) = \max(0, 1-yf(x))\]

위에 정리한 support vector classifier의 optimization 문제를 hinge loss와 ridge penalty를 이용한 표현으로 변환할 수 있다.

\[\text{minimize}_{\beta_0, \beta_1, \ldots, \beta_p} \left\{ \sum_{i=1}^n \ell_{\text{hinge}}(y_i, f(x_i)) + \lambda \sum_{j=1}^p \beta_j^2 \right\}\]

여기서 $f(x) = \beta_0 + \beta_1 x_1 + \cdots + \beta_p x_p$ 이다.

Hinge loss는 logistic regression의 loss function인 negative log-likelihood와 상당히 유사한 형태를 갖는다.

Kernels

Feature Expansion

어떤 data의 경우, linear classifier가 적합하지 않을 수 있다.

이러한 경우, feature의 transformation들을 통해 feature space를 확장하는 feature expansion을 통해 non-linear data를 linear하게 표현할 수 있다. (e.g. $\phi:(x_1,x_2) \rightarrow (x_1^2,\sqrt{2}x_1x_2,x_2^2)$)

Kernels

이러한 feature expansion은 두 가지 어려움이 존재한다. 첫번째는 feature space를 어떻게 확장해야 할 지에 대해 알기 어렵고, 두번째는 feature expansion에 의해 space의 dimension이 높아지는 경우 computation cost가 증가하기 때문이다.

자세한 설명은 생략하겠지만, support vector classifier의 optimization 문제를 Lagrangian dual form으로 표현하여 optimal solution을 찾기 위해서는 vector간 inner product를 계산해야만 한다.

예를 들어, $\phi:(x_1,x_2) \rightarrow (x_1^2,\sqrt{2}x_1x_2,x_2^2)$을 고려하자. 이 때, expansion 시킨 space에서의 vector간 inner product는 다음과 같다.

\[\phi(p) \cdot \phi(q) = (p_1^2, \sqrt{2} p_1 p_2, p_2^2)^T (q_1^2, \sqrt{2} q_1 q_2, q_2^2) = p_1^2 q_1^2 + 2 p_1 p_2 q_1 q_2 + p_2^2 q_2^2\]

간단한 expansion에서도 계산량이 늘어나는 것을 알 수 있다. 하지만, 이를 기존 vector의 inner product $p\cdot q$로 표현할 수 있다.

\[p_1^2 q_1^2 + 2 p_1 p_2 q_1 q_2 + p_2^2 q_2^2 = (p_1 q_1 + p_2 q_2)^2 = (p \cdot q)^2\]

즉, 특정한 feature expansion의 경우, vector를 모두 expansion 하여 계산하지 않아도 기존 dimension에서 충분히 inner product 값을 계산할 수 있다. 이러한 성질을 만족하는 mapping $\phi$을 이용하는 것을 kernel trick이라고 한다.

실제로 kernel은 vector간 similarity를 측정하는 function을 포괄적으로 지칭하는 용어이지만, 여기서의 kernel은 kernel trick을 만족하는 function으로 한정한다.

SVM에서 kernel의 종류는 무척 다양하고 주요한 연구 주제 중 하나이다. 다만 여기서는 널리 사용되는 scikit-learn의 SVM method에서 지원하는 kernel 종류에 대해서만 소개한다.

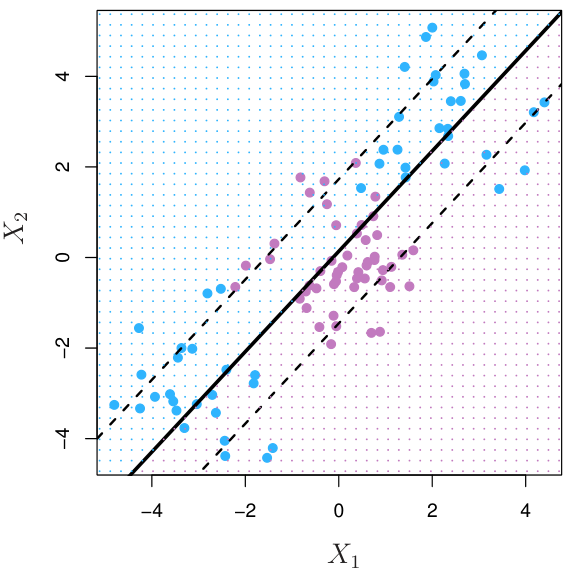
• Linear kernel

\[K(x_1, x_2) = x_1^T x_2\]

• Polynomial kernel

\[K(x_1, x_2) = (\gamma (x_1^T x_2) + \theta)^d\]

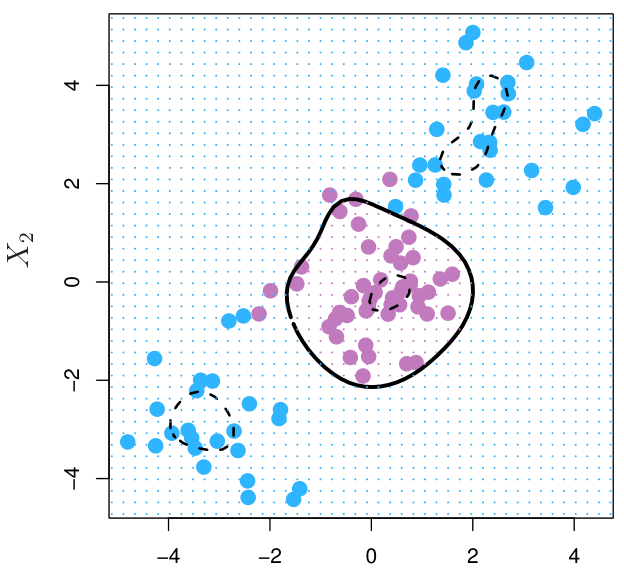
• Radial Basis Function(RBF) kernel

\[K(x_1, x_2) = \exp\left(-\gamma \|x_1 - x_2\|^2\right)\]

RBF kernel은 널리 사용되는 non-linear kernel 중 하나로, infinite dimension으로의 mapping이 가능하여 매우 유연한 hyperplane을 만들 수 있다.

• Sigmoid kernel

\[K(x_1, x_2) = \tanh(\gamma (x_1^T x_2) + \theta)\]

Multiclass Classification with SVMs

지금까지 정리한 SVM은 binary classification에 대한 문제를 푸는 방법에 대한 내용이었다. 만약 class의 개수 K가 2보다 크다면, 이를 풀기 위해서는 두 가지 접근법 중 하나를 택해야 한다.

• One vs All (OVA)
  1. 각 class 별로, ‘해당 class에 속하는지’ vs ‘해당 class에 속하지 않는지’를 결정하는 K개의 서로 다른 SVM classifier $\hat{f}_k(x)$들을 학습한다.
  2. 새로운 data $x^\ast$에 대해서 가장 큰 $\hat{f}_k(x^\ast)$ 값을 갖는 class k로 분류한다.
• One vs One (OVO)
  1. 모든 class pair에 대해서 $n \choose 2$개의 classifier $\hat{f}_{kl}(x)$을 학습한다.
  2. 새로운 data $x^\ast$에 대해서 pairwise competition에서 가장 많이 승리한 class로 할당한다.

OVO 방법이 단연코 높은 computation cost가 필요하지만, K가 크지 않은 경우 OVO 방법이 OVA에 비해 일반적으로 더 높은 성능을 보여준다.