Stochastic Gradient Descent

• Remind: Calculus Backgrounds

Gradient Descent

Common machine learning methods find the value that minimizes the loss function using the steepest descent method or gradient descent (GD).

\[\theta^{(t+1)} = \theta^{(t)} - \eta_t g_t\]

Here, when the gradient is calculated using all the training data, it is called (full) batch GD.

\[g_t = \frac{1}{N} \sum_{i=1}^N \nabla_{\theta} \mathcal{L}(x_i, y_i; \theta)\]

While GD is a good approach, the loss surface us generally non-quadratic, highly non-convex, and very high-dimensional. Therefore, calculating gradient itself is difficult, and there is a high probability of getting stuck at local minima or saddle points (+ flat region). Also, since the dataset is very large, the training process becomes quite slow due to the need to compute the gradient for all data.

Stochastic Gradient Descent

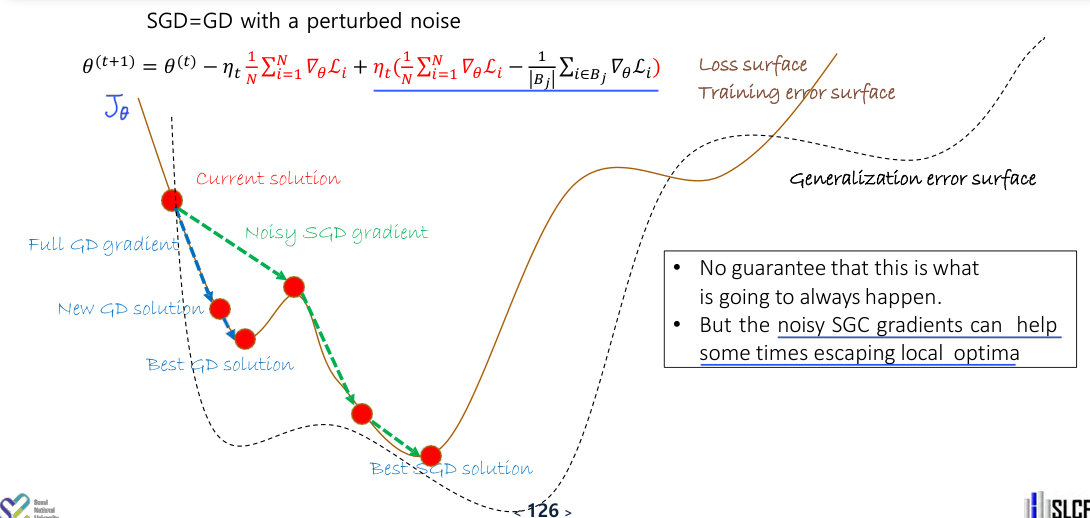
In GD, the gradient $g_t$ is essentially an approximation of the gradient of the cost function computed using the law of large number.

\[J^*(\theta)=E_{(x,y)\sim P_{data}}[L(y,f(x;\theta))] \\ \Rightarrow \nabla_\theta J(\theta) = E[\nabla_\theta L] \approx \frac{1}{N} \sum_{i=1}^N \nabla_\theta L(x_i,y_i;\theta)\]

Stochastic gradient descent (SGD), then, calculates this approximation using fewer samples (minibatch).

\[\theta^{(t+1)} = \theta^{(t)} - \frac{\eta_t}{|B_j|} \sum_{i \in B_j} \nabla_{\theta} \mathcal{L}_i, \quad B_j = \text{sample}(D).\]

Looking at previous studies, minibatches typically range from 32 to 256 samples, but in practice, it is best to determine this based on the model’s computing power.

SGD is Often Better

SGD is naturally faster than GD, and additionally, it often performs better. This is because SGD approaches the minimum in a noisier manner than GD, which helps avoid getting stuck in local optima.

Noisy gradients can be viewed as acting as regularization.

Moreover, while GD aims to find the optimal value for the data itself rather than the data distribution, SGD can be seen as using new data generated from the data distribution at each instance for training, which tends to minimize generalization error more effectively than GD.

Therefore, it is generally better to shuffle the data before dividing it into minibatches to ensure that the distribution between minibatches is similar.

SGD is particularly suitable for datasets that change over time. (GD tends to be biased towards past samples.)