Solving MDP

• 참고
  • MDP
  • Bellman Equation and Optimality

MDP를 푼다는 것은 optimal policy $\pi_\ast$를 구한다는 것과 동일하며, 이는 결국 Bellman optimality equation를 푸는 것과 동일하다. 여기서는 non-linear equation인 Bellman optimality equation를 푸는 알고리즘에 대해서 소개한다.

Prediction and Control

우선 알고리즘을 소개하기 전, prediction과 control에 대해 정의하자.

• Prediction: 주어진 MDP와 policy $\pi$에 대해서, value function $V_\pi$를 찾아내는 것

• Control: 주어진 MDP에 대해, optimal policy $\pi_\ast$ 또는 optimal value function $V_{\pi_\ast}$를 찾아내는 것

Iterative Policy Evaluation

Policy evaluation은 prediction 방법 중 하나로, 일반적으로 dynamic programming을 통해 이를 진행한다. 특히, Bellman expectation equation을 iterative하게 적용하여 converge 시키는 방법을 이용하기 때문에 iterative policy evaluation이라고도 한다.

해당 알고리즘은 다음과 같이 동작한다.

1. 모든 state에 대해 임의의 state-value를 생성한다.

2. Value function에 대한 Bellman expectation backup을 반복적으로 적용한다.

   \[V^{k+1}(s) = \sum_{a \in \mathcal{A}} \pi(a \mid s) \left( R_{s}^{a} + \gamma \sum_{s' \in \mathcal{S}} P_{ss'}^{a} V^{k}(s') \right)\] \[\left( V^{k+1} = R^{\pi} + \gamma P^{\pi} V^k \right)\]
   • Backup: 현재 state value를 다음 state의 value와 reward에 따라 update하는 것을 의미
3. Value function이 수렴하면 종료
   • $\max_s \vert V^k(s) - V^{k-1}(s) \vert \leq \delta$ for a small $\delta > 0$

위 과정은 action-value function $Q(s,a)$에 대해서도 동일하게 적용된다.

Iterative policy evaluation은 임의의 value 값에 대해서도 convergence가 보장이 되어있다. 이는 contraction mapping theorem에 의한 것으로, 자세한 설명은 생략한다.

Policy Improvement

Policy evaluation을 통해 얻은 현재 policy $\pi$의 value function을 이용해 더 나은 policy $\pi’$을 얻을 수 있다. 이를 policy improvement라고 한다.

Policy improvement는 무척 간단한데, 단순하게 현재 value function $V_\pi$ 또는 $Q_\pi(s,a)$ 기준으로 greedy하게 행동하는 policy를 얻으면 된다.

\[\pi'(s) = \arg\max\limits_{a \in \mathcal{A}} Q_\pi(s,a)\]

이렇게 얻은 새로운 policy $\pi’$는 모든 state에 있어서 기존 policy $\pi$보다 같거나 더 높은 value를 가지도록 행동하기 때문에, 기존 policy보다 더 나은 policy임을 쉽게 알 수 있다.

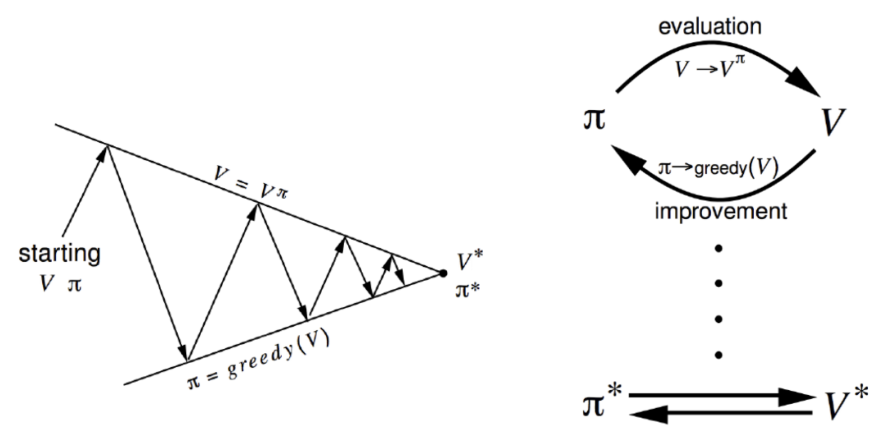
Policy Iteration

Policy iteration이란 policy evaluation과 policy improvement의 반복되는 과정을 말한다. 즉, 현재 policy에서 value function을 얻고, 더 나은 policy를 얻고, 이를 이용해 다시 value function을 얻고, 다시 더 나은 policy를 얻는 과정을 계속적으로 반복한다.

Policy iteration 과정에서 가장 시간이 많이 소요되는 부분은 policy evaluation이다. 하지만, Bellman 연산자는 MDP에서 convergence가 보장되어 있기 때문에, 꼭 policy evaluation을 끝까지 수행하지 않아도 policy iteration을 통해 optimal policy를 얻을 수 있다.

단, 모든 state가 1번씩은 update되어야 optimal policy에 도달할 수 있다.

Value Iteration

Value iteration은 Bellman optimality backup을 반복적으로 적용하는 것으로 optimal policy를 얻는 control 방법이다.

\[V^{k+1} = \max_{a \in \mathcal{A}} \left(R + \gamma P V^k\right)\]

Value iteration은 policy iteration과 다르게 policy를 따로 참조하지 않고, $\max$ 함수를 통해 이를 대신한다.

Value iteration은 1-step policy evaluation + argmax policy improvement로 볼 수 있다.

Value iteration 역시 contraction mapping thoerem에 의해 convergence가 보장되어 있다.

Summary

Problem	Bellman equation	Algorithm
Prediction	Bellman expectation equation	Iterative policy evaluation
Control	Bellman expectation equation + Greedy policy improvement	Policy iteration
Control	Bellman optimality equation	Value iteration

$m$개의 action과 $n$개의 state가 있을 때, state-value function $V(s)$를 이용한 알고리즘은 $O(mn^2)$, action-value function $Q(s)$를 이용한 알고리즘은 $O(m^2n^2)$의 시간복잡도 (iteration 당)을 갖는다.