Sequence-to-Sequence and Attention
Sequence-to-Sequence (Seq2seq)
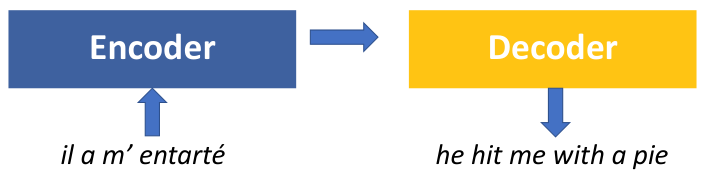
Sequence-to-Sequence (seq2seq)는 encoder-decoder structure라고도 불리우는 모델이자 일종의 framework이다. Seq2seq은 input (또는 source) sequence를 입력받는 encoder 부분과 output (또는 target) sequence를 생성하는 decoder 부분으로 나뉘어진다.
seq2seq을 encoder와 decoder 구조를 갖지만, 그 encoder와 decoder가 어떤 형태로 구성되어야 하는지, parameter 계산에 관한 어떤 방법론이 필요한지 등에 대한 제한이 따로 없다. 즉, 일반적인 encoder-decoder 구조를 갖는 모델은 seq2seq framework를 갖는다고 말할 수 있다.
Seq2seq with LSTM
일반적으로 seq2seq에서 encoder와 decoder는 여러 layer를 갖는 RNN, LSTM 모델로 구현된다.
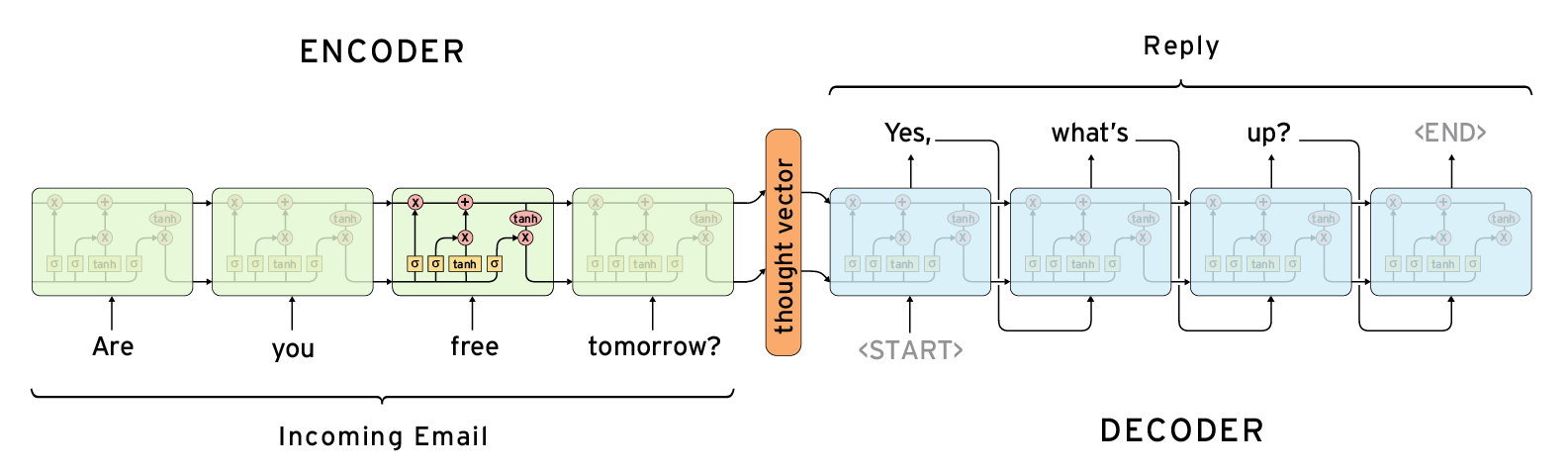
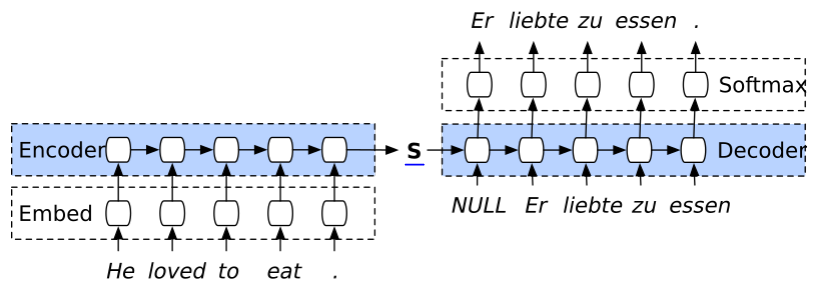
예를 들어, LSTM을 통해 encoder와 decoder가 구현되었다고 하자. 이 때의 seq2seq 모델은 다음과 같이 표현된다.
Encoder에서는 source sentence를 입력받을 때, 각 단어를 순차적으로 input으로 받고서 최종적으로 모든 input을 하나의 vector로써 나타낸다. 이 때의 vector를 code vector라고 불리운다 (또는 context vector, thought vector 등 다양한 이름으로 불린다).
Decoder에서는 encoder가 생성한 code vector와 시작을 나타내는 특수 문자열 (‘START’)를 입력받아 decoding을 시작한다. 이 때, decoder는 특정 시점 $t$의 output이 $t+1$의 input이 된다는 특징이 있다. 즉, 위 예시에서 ‘Yes,’라는 첫번째 output은 decoder의 input이 되며, 이를 통해 생성된 output ‘what’s’는 그 다음 input이 된다.
즉, encoder는 source sequence를 끝까지 읽고 하나의 vector로 정보를 압축하는 역할을 하고, decoder는 압축된 input 정보와 지금까지 생성해 낸 sequence의 정보를 활용해서 반복적으로 output sequence를 생성하는 역할을 한다.
Seq2seq은 encoder와 decoder가 한번에 forward 및 backward propagation이 이루어지는 구조를 갖고 있다. 즉, end-to-end 시스템이기에 사용자가 더 쉽게 사용할 수 있다는 장점을 갖는다.
Encoder와 decoder는 기본적으로 parameter를 공유하지 않는다. 따라서, 서로 다른 모델로 구현되어도 무방하다. 결국 encoder와 decoder의 역할은 구분되어 있기에, encoder를 RNN으로, decoder를 LSTM으로 구현하여도 무방하다.
Beam Search
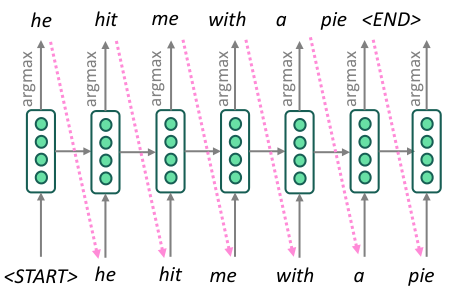
Decoder가 output을 생성하는 과정을 조금 더 자세하게 살펴보자.
기본적으로 decoder는 most probable한 target sequence를 생성하는 것이 목적이다. 만약 length가 $T$인 output을 생성한다고 할 때, 가능한 output의 가짓수가 $V$로 한정되어 있다고 하더라도 $V^T$의 경우의 수를 비교해야만 가장 높은 probability를 갖는 target sequence를 찾을 수 있다.
이러한 현실적인 한계를 고려하면, greedy decoding을 decoding 방법으로 선택할 수 있다. 이는, 미래 시점의 output을 고려하지 않고, 현재 시점에서 가장 높은 probability를 갖는 (argmax) output만을 선택하는 것이다.
하지만, 이러한 greedy solution은 optimal solution과 거리가 먼 경우가 꽤나 있다. 특히, 자연어와 같이 sequence의 마지막 부분이 결과에 큰 영향을 미치는 경우가 많은 경우에는 더러 그렇다 (사람 말은 끝까지 들어야 한다!).
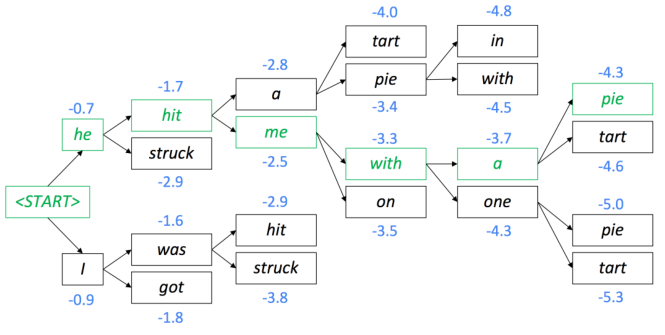
따라서, 대부분의 decoder는 beam search decoding을 수행한다. 이는, argmax output만을 선택하고 끝내는 것이 아니라, output을 생성하면서 top-$k$ path를 가지고 가면서 path에 대한 score의 누적값으로 output을 선택하는 것이다. 이 때의 $k$를 beam size라고 한다.
이 때의 score는 probability에 대한 negative log값을 선택하는 것이 일반적이다.
위 예시를 살펴보면, 첫 output으로 선택된 ‘he’와 ‘I’를 모두 저장해두고, 각각에 대해서 두번째 decoding의 input으로 삼는다. 이 때, ‘he’는 ‘hit’과 ‘struck’을, ‘I’는 ‘was’와 ‘got’을 각각의 output으로 선택한다. 하지만 이 때 path가 4개가 되므로, 누적 score가 가장 높은 두개의 path: ‘he hit’과 ‘I was’를 남겨두고 나머지는 버린다.
위와 같은 작업을 반복하고, 최종적인 top-2 path 중 더 높은 score를 갖는 path를 최종 target sequence로 선택한다.
Seq2seq with Attention
하지만, 단순한 seq2seq 모델에는 information bottleneck이라는 큰 문제가 있다. 이는, 모든 input sequence가 하나의 fixed-length vector로 표현된다는 것인데, 아무리 긴 input일지라도 결국 하나의 vector로 표현된다는 한계는 올바른 decoding을 어렵게하는 큰 어려움이다.
또한, RNN 구조의 모델들이 갖는 고질병 중 하나인 vanishing gradient 문제 역시 여전히 신경써야할 부분이다.
이러한 한계를 극복하기 위해 고안된 방법론이 바로 attention이다. Attention은 decoder의 각 decoding 단계에서, encoder에서 source sequence들과의 direct connection을 통해 input의 모든 정보를 온전히 활용하여 output을 산출하는 것을 말한다. 즉, output을 생성하는 과정에서 input의 모든 정보를 attention한다는 점에서 이러한 이름이 붙게 되었다.
Attention Mechanism
아래와 같이 불어를 영어로 번역하는 machine translation task을 통해 attention mechanism을 자세히 알아보자.
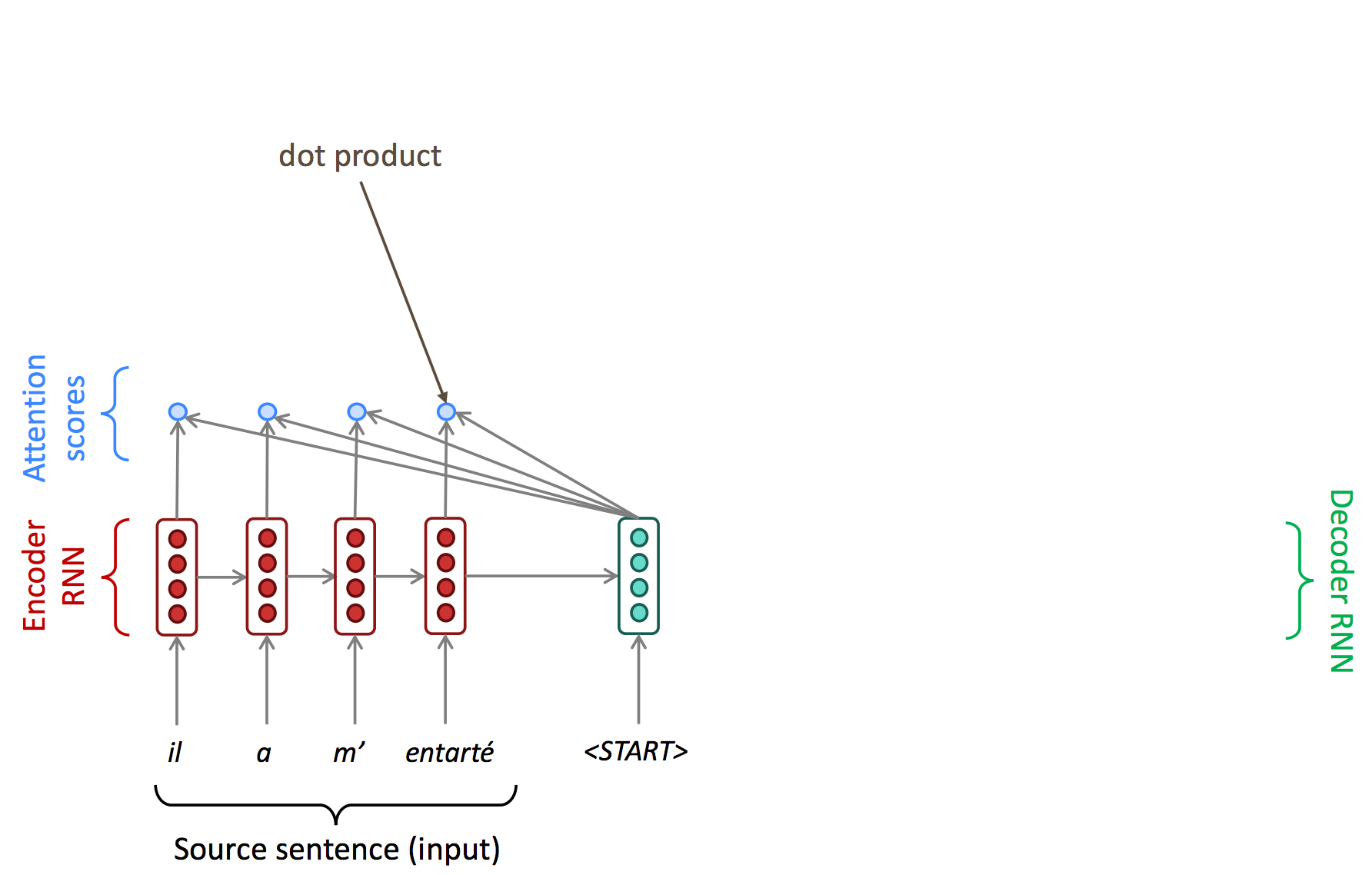
기존의 seq2seq 모델의 경우 source sequence의 마지막 단어 ‘entarté’를 거쳐 생성된 context vector와 decoding의 시작을 알리는 특수단어 ‘START’만을 이용해 output을 생성했다.
하지만, attention을 이용한 decoding은 우선 시작하는 시점에 source sequence의 모든 단어와 attention score를 각각 계산한다.
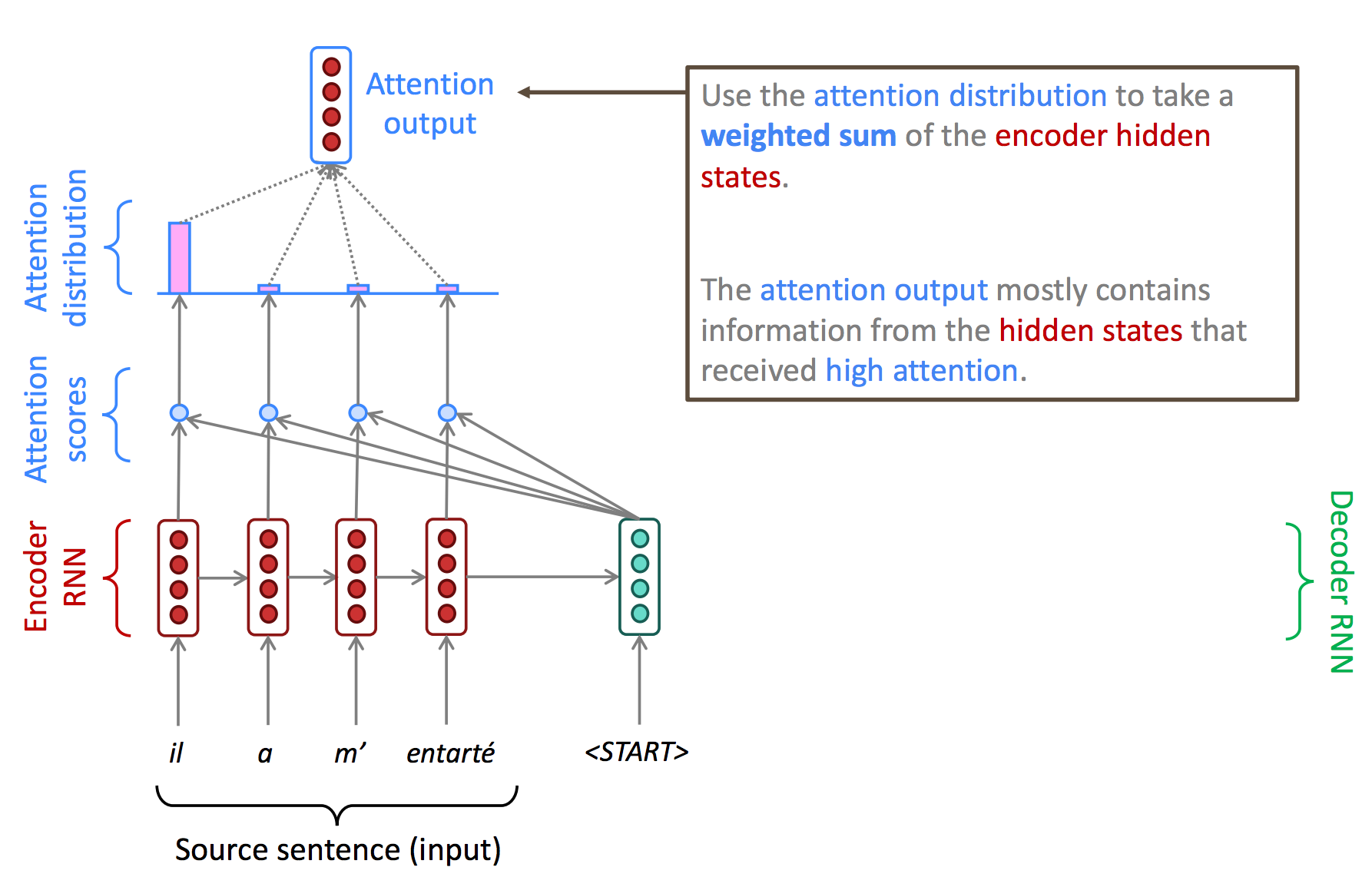
이렇게 계산된 attention score를 통해 attention distribution을 생성하고, 이를 기반으로 attention output을 생성한다. Attention output은 일반적으로 attention distribution과 encoder hidden state의 weighted sum으로 구한다.
즉, attention output은 주로 높은 attention score를 갖는 정보의 hidden state로 구성된다.
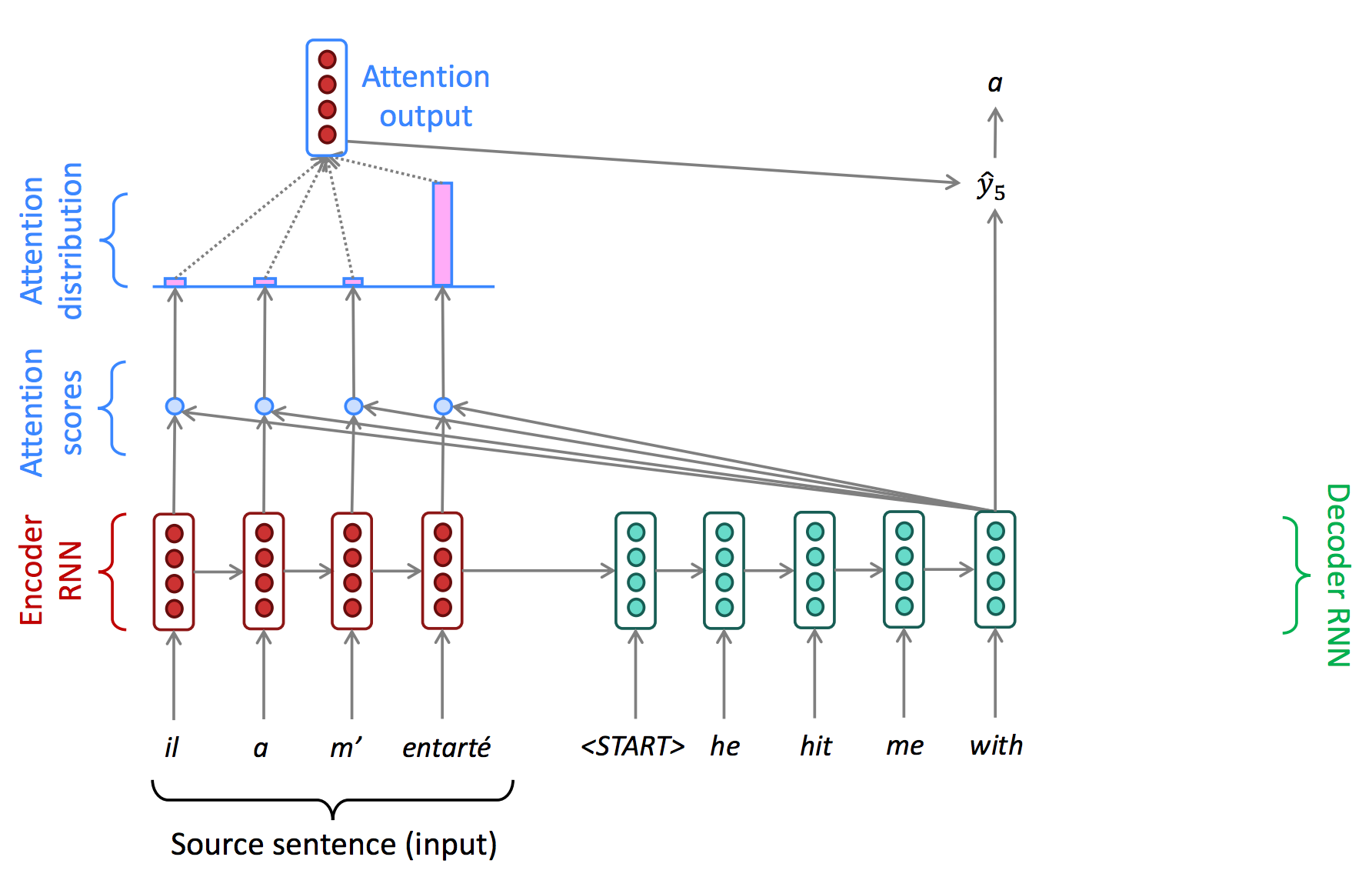
이렇게 생성된 attention output과 decoder의 hidden state를 concatenate한 값을 최종 decoder의 output으로 설정한다.
Attention in Math
위 과정을 수리적으로 생각해보자.
Encoder로 부터 얻은 hidden states $h_1, \ldots, h_N \in \mathbb{R}^h$를 가정하자.
Time step $t$에서, decoder의 hidden state를 $s_t \in \mathbb{R}^h$라고 하자.
우선 attention score $e^t$를 아래와 같이 얻을 수 있다.
\[e^t = \left[ s_t^T h_1, \ldots, s_t^T h_N \right] \in \mathbb{R}^N\]Attention score $e^t$에 softmax를 적용하여 attention distribution $\alpha^t$를 얻는다.
\[\alpha^t = \text{softmax}(e^t) \in \mathbb{R}^N\]Attention distribution $\alpha^t$을 이용하여 encoder hidden state $h_t$와의 weight sum을 통해 attention output $a_t$를 얻는다.
\[a_t = \sum_{i=1}^N \alpha_i^t h_i \in \mathbb{R}^h\]Attention output $a_t$과 decoder hidden state $s_t$를 concatenate하고, 이후는 일반적인 seq2seq model과 동일하게 진행한다.
\[[a_t; s_t] \in \mathbb{R}^{2h}\]
Query, Key, and Value
Attention 또는 이후에 다룰 self-attention의 내용을 보면, query, key, 그리고 value라는 단어가 자주 등장한다. Query란 현재의 상태나 입력에 대한 질문을, key와 value는 query에 대한 답을 얻기 위해 사용되어지는 key-value pair로 볼 수 있다. 일반적으로 query가 주어지면 우선적으로 key를 조사하여 가장 적합한 (유사한) key를 구하고, 그 key와 연결된 value를 통해 최종적인 값을 얻게된다.
Attention에서의 query, key, value 역시 위와 유사하게 동작한다. Query가 주어지면, 각 key와의 유사도를 구하고, 이를 각 key와 연결된 value와 곱해주고, 그 값들에 대한 합을 통해 query에 대한 답을 얻는다. 즉, attention 모델에서 query는 decoder의 hidden state $s_t$, key와 value는 encoder의 hidden state $h_t$, 그리고 최종적인 결과물은 attention output $a_t$가 되는 것이다.
Attention variations
일반적으로 attention score $e^t$를 구하는 과정은 dot-product를 사용한다. 이를 basic dot-product attention 이라고 한다. 하지만, 이 외에도 attention score를 구하는 방법은 다양하게 있으며 여기서는 두 가지 다른 방법을 소개한다.
- Multiplicative attention: $e_i = s^T W h_i \in \mathbb{R}$
- 여기서 $W$는 weight matrix로 학습되어지는 값이다.
- Additive attention: $e_i = v^T \tanh(W_1 h_i + W_2 s) \in \mathbb{R}$
- $W_1, W_2, v$는 parameter로 학습되어지는 값이다.
- $W_1, W_2$의 dimension은 hyperparameter이다.
Attention is Great
Attention 방법을 통해 seq2seq framework를 이용한 학습, 특히 NLP 분야에서 큰 발전을 이루었다.
Attention을 통해 information bottleneck 이슈를 해결하였고, direct connection으로 인해 vanishing gradient 문제 역시 완화하였다.
또한, attention score 및 distribution을 분석함으로써, 각 output이 input의 어떤 부분을 더 참조하였는지를 알 수 있게 되어 interpretability를 갖기도 한다.
하지만, attention은 기본적으로 encoding의 모든 부분은 순차적으로 처리해야한다는 한계가 있어 병렬 처리에 있어서는 약간의 아쉬움이 있었다. 이러한 아쉬움을 개선하고자 self-attention이라는 기술이 개발되었고, 이는 현재 가장 널리 사용되는 transformer architecture의 핵심 기술이 된다.