Regularization
Regularization
Regularization은 model의 flexibility를 조절하여 overfitting을 방지하고, model의 성능을 향상시키기 위해 사용되는 기법을 말한다. 주로 regression analysis와 machine learning에서 사용된다.
Regularization은 일반적으로 model의 objective function에 penalty term을 추가하여 feature의 coefficeint를 줄이거나, 0으로 만드는 방식으로 작동한다. 이러한 관점에서 shrinkage라고도 한다.
Regularization 적용 시에, coefficient의 variance 역시 크게 줄어드는 것이 알려져있다.
대표적인 regularization 방법으로는 ridge regression, lasso regression, 그리고 elastic net이 있다.
Ridge Regression
일반적인 multivariable linear regression 문제를 고려하자. 이는 $\text{RSS} = \sum_{i=1}^n \left( y_i - \beta_0 - \sum_{j=1}^p \beta_j x_{ij} \right)^2$을 minimize하는 $\hat{\beta}$을 찾는 문제로 볼 수 있다.
이 때, Ridge regression은
\[\sum_{i=1}^n \left( y_i - \beta_0 - \sum_{j=1}^p \beta_j x_{ij} \right)^2 + \lambda \sum_{j=1}^p \beta_j^2 = \text{RSS} + \lambda \sum_{j=1}^p \beta_j^2\]을 minimize하는 $\hat{\beta}^R$을 찾는 문제를 말한다.
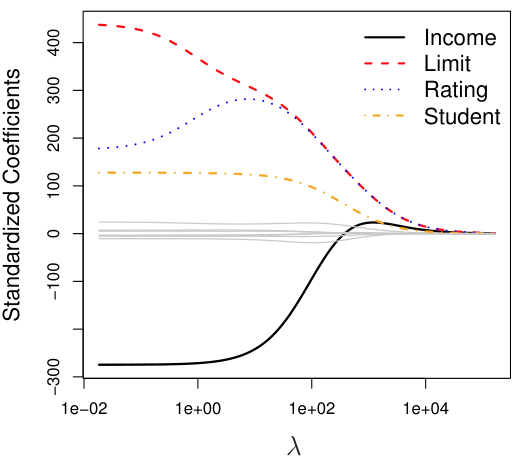
여기서 $\lambda \sum_{j=1}^p \beta_j^2$ 은 shrinkage penalty term으로, 불필요한 $\hat{\beta_j}$을 0에 가깝게 만들어주는 역할을 한다. Penalty term이 제곱 형태를 띄고 있으므로, Ridge regression은 이를 $\ell_2$-regularization 이라고도 부른다.
따라서, hyperparameter $\lambda \ge 0$를 조절함으로써 model의 flexibility를 조절할 수 있다. ($\lambda$가 클수록 flexilibity가 작아진다.)
일반적인 regression의 경우 feature $X_j$의 크기가 다 다르더라도, 해당 feature의 coefficient $\hat{\beta_j}$에 녹여져 있어서 크게 문제가 없다 ($X_j \hat{\beta_j}$이 일정).
하지만, ridge regression과 같은 regularization 방법의 경우 shrinkage penlaty term이 존재하므로 feature들에 대해 모두 standardization을 진행한 후에 학습을 하는 것이 좋다.
Lasso Regression
Ridge regression은 한 가지 큰 단점이 있는데, 바로 모든 features들이 (비록 아주 작은 coefficient를 갖더라도) final model에 포함된다는 것이다. 이로 인해 feature의 수가 많은 경우, 여전히 overfitting 이슈가 존재하고 interpretability가 떨어지는 단점이 존재한다.
Lasso regression은 feature selection의 기능까지 있는 regularization 방법으로,
\[\sum_{i=1}^n \left( y_i - \beta_0 - \sum_{j=1}^p \beta_j x_{ij} \right)^2 + \lambda \sum_{j=1}^p |\beta_j| = \text{RSS} + \lambda \sum_{j=1}^p |\beta_j|\]을 minimize하는 $\hat{\beta}^L$을 찾는 문제를 말한다. 여기서의 penalty term은 $\lambda \sum_{j=1}^p \vert \beta_j \vert$이 되며, penalty term의 형태에 의해 Lasso regression은 $\ell_1$-regularization이라고도 불린다.
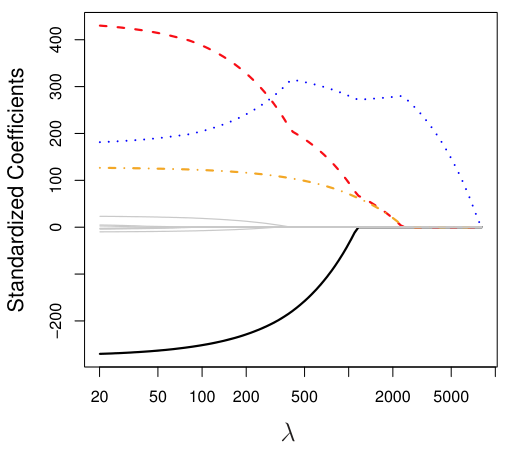
Lasso regression은 ridge와 다르게, 불필요하다고 판단되는 feature의 $\hat{\beta_j}$를 0으로 만든다. 따라서, lasso regression은 sparse model을 생성한다고 말할 수 있다.
Differences Between Ridge and Lasso
Ridge regression은 다음 optimization 문제의 Lagrangian form으로 볼 수 있다. (여기서 $s$는 $\lambda$와 같이 regularization의 정도를 결정한다.)
\[\text{minimize}_{\beta} \quad \sum_{i=1}^n \left( y_i - \beta_0 - \sum_{j=1}^p \beta_j x_{ij} \right)^2 \quad \text{subject to} \quad \sum_{j=1}^p \beta_j^2 \leq s\]비슷하게, Lasso regression의 solution은 다음 optimization의 solution이 된다.
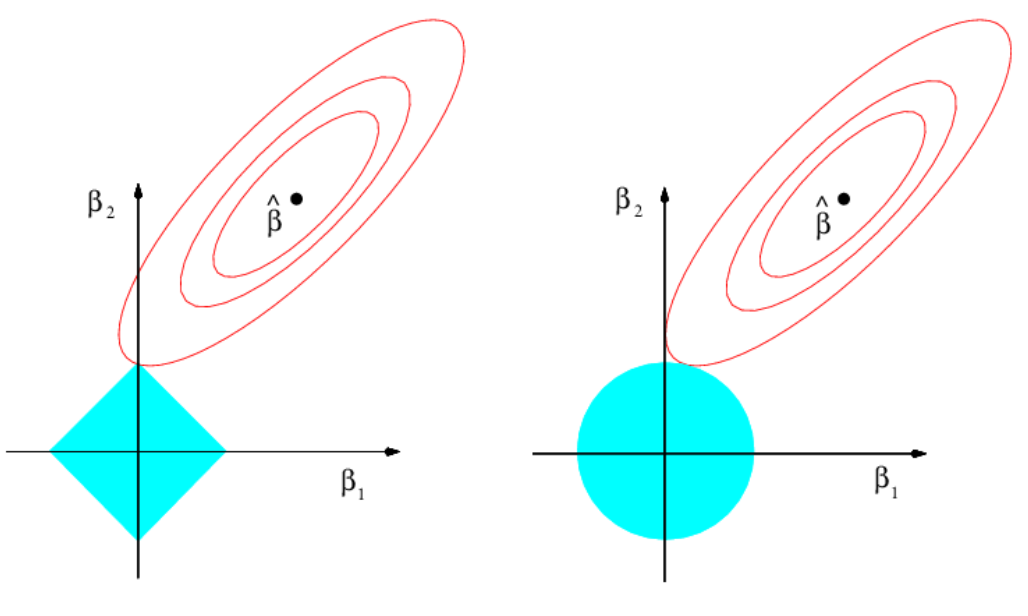
\[\text{minimize}_{\beta} \quad \sum_{i=1}^n \left( y_i - \beta_0 - \sum_{j=1}^p \beta_j x_{ij} \right)^2 \quad \text{subject to} \quad \sum_{j=1}^p |\beta_j| \leq s\]두 optimization 문제를 그림과 같이 표현하면 각각 아래와 같다 (왼쪽: Lasso, 오른쪽: Ridge).
즉, solution space의 형태의 차이로 $\hat{\beta}^L$은 많은 경우 0으로, $\hat{\beta}^R$은 0이 아닌 값으로 나타난다.
이러한 이유로, 일반적으로 Lasso가 Ridge보다 더 좋은 performance를 보인다고 알려져 있으나, 절대적 우열관계를 가지는 것은 아니므로, cross-validation 방법 등을 통해서 regularization 방법을 결정하는 것이 합리적이다.
Elastic Net
Elastic net은 Ridge regression과 Lasso regression의 hybrid model로써,
\[\sum_{i=1}^n \left( y_i - \beta_0 - \sum_{j=1}^p \beta_j x_{ij} \right)^2 + \lambda_1 \sum_{j=1}^p \beta_j^2 + \lambda_2 \sum_{j=1}^p |\beta_j|\]을 minimize하는 $\hat{\beta}^E$을 찾는 문제를 말한다.
이 때, Ridge penalty term는 correlation이 높은 feature들의 coefficient를 조절하여 multicollinearity를 줄여줄 수 있는 인자, Ridge penalty term는 model의 sparsity를 조절하는 인자가 된다.
Elastic net은 우수한 performance를 보인다는 것이 empirical하게 알려져 있다.