Recurrent Neural Network
Recurrent neural network (RNN)은 sequential data를 처리하는 것에 특화된 neural network로, 자연어 처리(natural language processing, NLP), 기계 번역(machine translation) 등 다양한 분야에서 사용된다.
기존의 FNN은 고정된 크기의 input과 output을 다루는 데 적합하지만, sequential data 또는 time-series data의 경우 data의 크기를 한정하는 것은 큰 제약이 된다. 또한, FNN의 경우 data가 independent하다는 가정이 있으나, sequential data는 data 사이의 time-dependency가 있으므로 과거 시점의 data를 고려할 수 있어야 한다.
Basic RNN
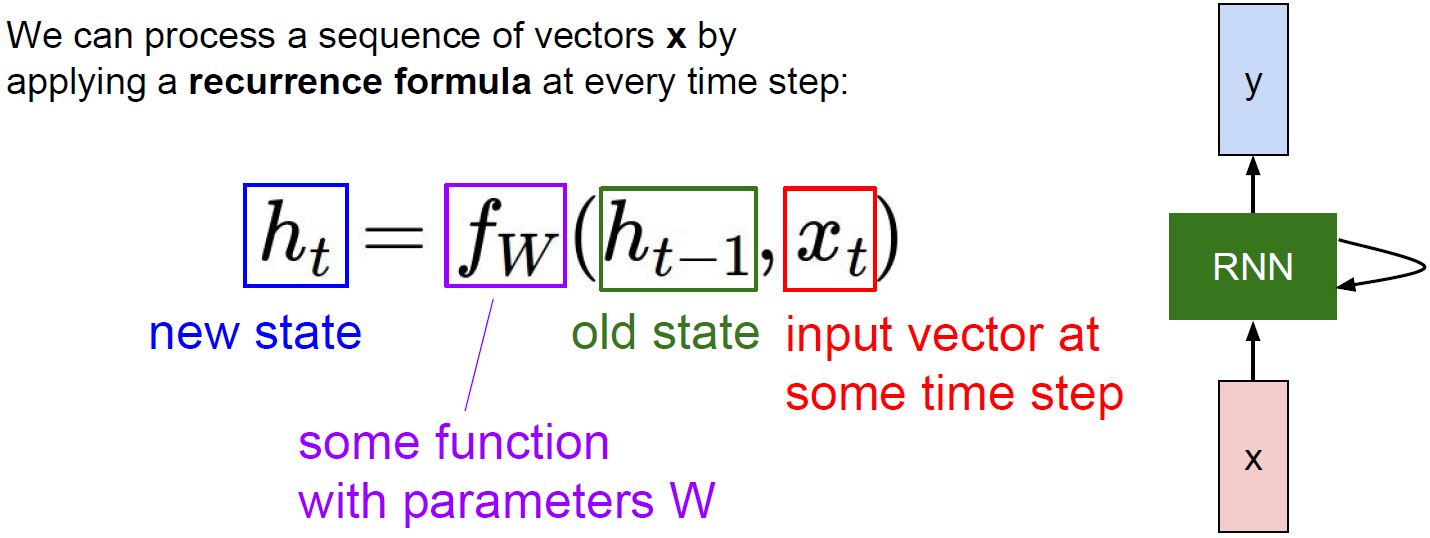
RNN은 아주 아래와 같이 아주 단순한 구조를 가지고 있다.
$h_t$는 hidden state 또는 hidden vector로 불리며, 현재 시점의 input $x_t$와 이전 시점의 hidden state $h_{t-1}$을 동시에 input으로 받는다. 즉, 현재와 과거의 정보를 모두 가져와 output을 생성한다.
위 과정을 수식으로 표현하면 다음과 같다.
\[h_t = f_W(h_{t-1}, x_t)\]이 때, activation function을 tanh로 사용하면 다음과 같이 풀어 쓸 수 있다.
\[\begin{aligned} h_t &= \tanh (W_{hh}h_{t-1} + W_{xh}x_t) \\ y_t &= W_{hy}h_t \end{aligned}\]Computation Graph of RNN
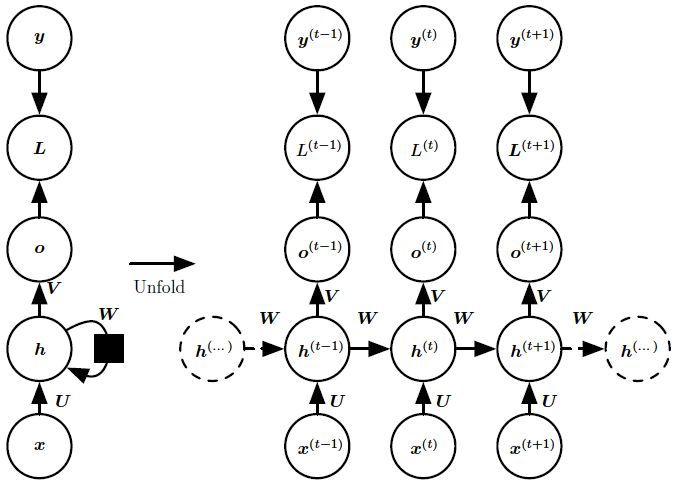
RNN은 동일한 parameter를 모든 시점에서 sharing하면서 사용하며, 이를 computation graph로 나타내면 다음과 같다. 여기서 ‘L’은 최종적인 작업 (classification, generation 등)을 위한 추가 layer을 의미한다.
Types of RNN
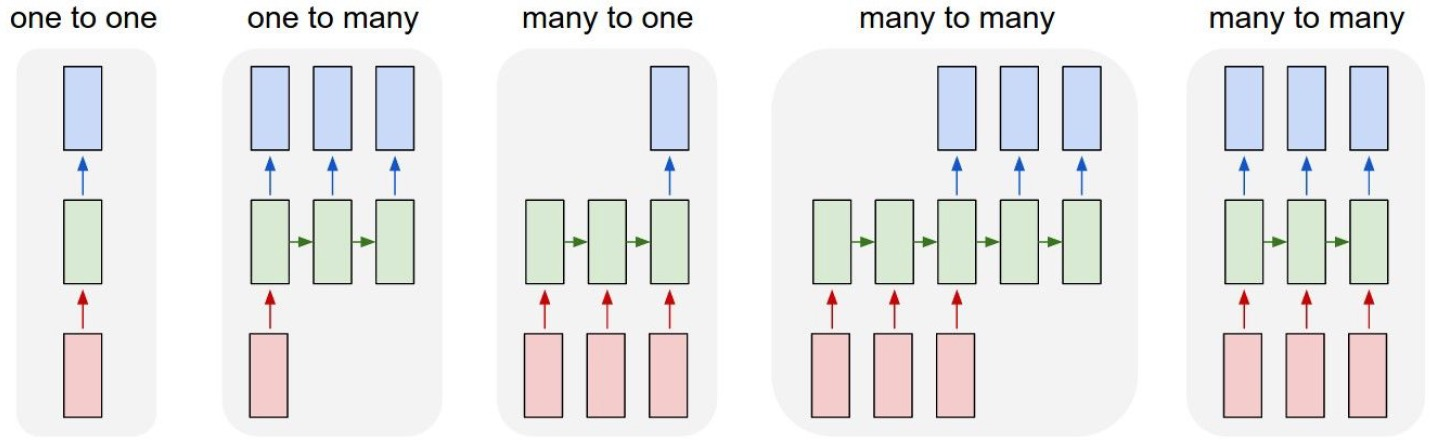
RNN은 input과 output의 관계에 따라 다음과 같이 분류될 수 있다.
각 케이스의 예시로는 다음과 같은 것들이 있다.
- one-to-many: image captioning
- many-to-one: sentiment classification
- many-to-many: machine translation, video classification on frame level
Forward/BackProp in RNN
위의 RNN의 computation graph를 활용하여 RNN에서의 학습이 어떻게 이루어지는지 확인해보자.
우선 RNN의 계산 과정을 보다 엄밀하게 표현하면 다음과 같이 쓸 수 있다.
\[\begin{aligned} h_t &= \tanh (b_h + W_{hh}h_{t-1} + W_{xh}x_t) \\ o_t &= b_o + W_{ho}h_t \\ y_t &= \text{softmax} (o_t) \end{aligned}\]이 때, 최종 loss는 각 time step에서의 loss를 모두 더한 값이 된다.
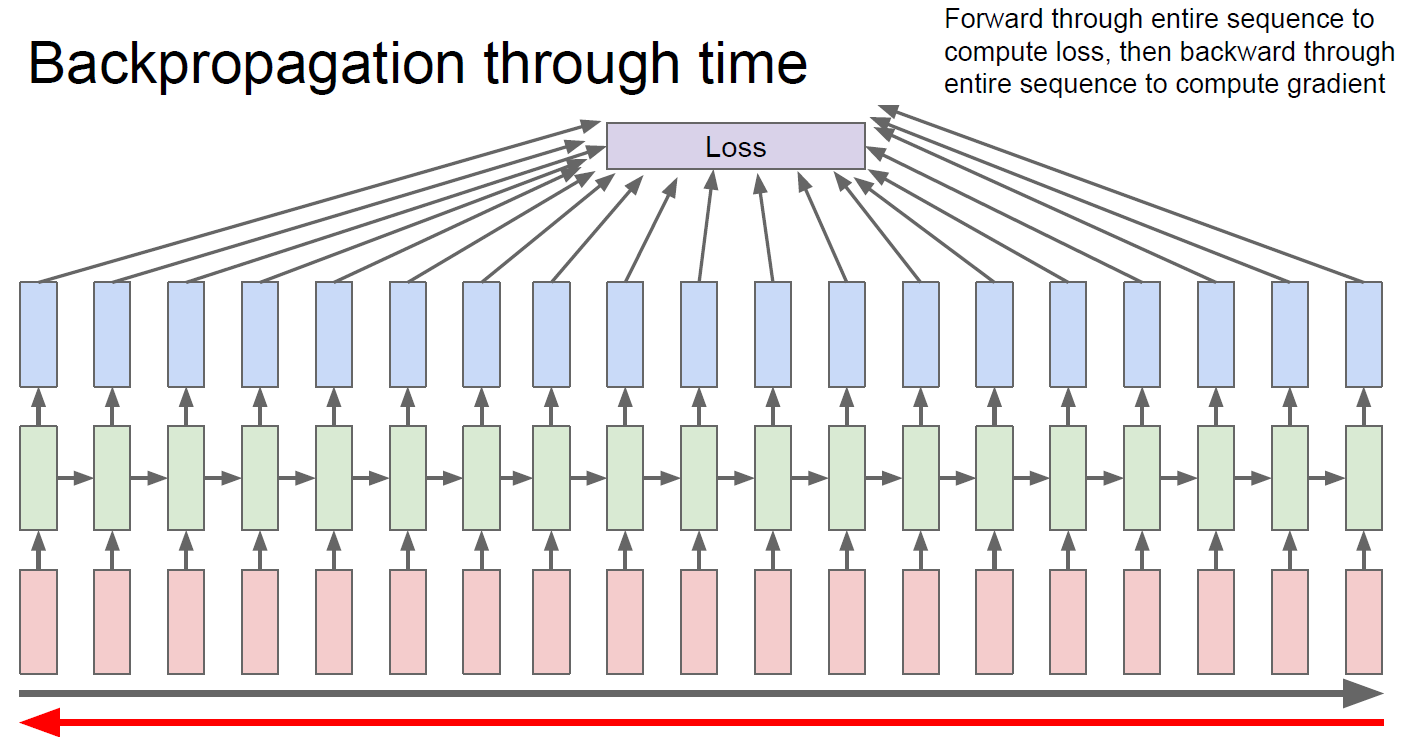
\[\begin{aligned} L(\{x_1,\dots,x_T \}, \{y_1,\dots,y_T \}) &= \sum_t L_t \\ &= -\sum_t \log p_{model} (y_t \mid \{x_1,\dots,x_T \}) \end{aligned}\]이렇게 구한 loss 값을 이용해 각 parameter를 update하기 위해서는 back propagation through time (BPTT)를 이용한다.
BPTT는 기본적으로 backprop과 동일하게 진행되나, 특정 time step에서의 gradient가 이전 step에서의 값에 의해서도 영향을 받기 때문에 각 time step에서의 parameter gradient를 모두 계산해야 한다.
\[\frac{\partial L}{\partial h_t} = \frac{\partial L}{\partial h_{t+1}} \frac{\partial h_{t+1}}{\partial h_t} + \frac{\partial L_t}{\partial h_t}\]위 chain rule을 반복적으로 적용하게 되면, 결국 time = 0이 될 때까지 gradient 계산이 수행되어야 한다.
BPTT의 계산량을 감소시키기 위해 Truncated-Backpropagation Through Time(생략된-BPTT)를 사용하기도 한다.
이렇게 계산된 각 time step의 gradient를 모두 더해 최종적인 parameter $W$의 gradient를 구하고, 이를 이용해 parameter update를 진행한다.
\[\frac{\partial L}{\partial W} = \sum_t \frac{\partial L_t}{\partial W}\]Bidirectional RNN
기본적으로 RNN은 causal structure를 갖고 있다. 즉, time step $t$에서는 과거 정보 $x_1, \dots, x_{t-1}$와 현재 정보 $x_t$만을 참조할 수 있다. 그러나, NLP와 같은 분야에서는 input sequence의 전체를 보고서 현재 시점의 output을 만들어내는 것이 중요할 수 있다 (e.g. 문장의 빈 칸 맞추기 등).
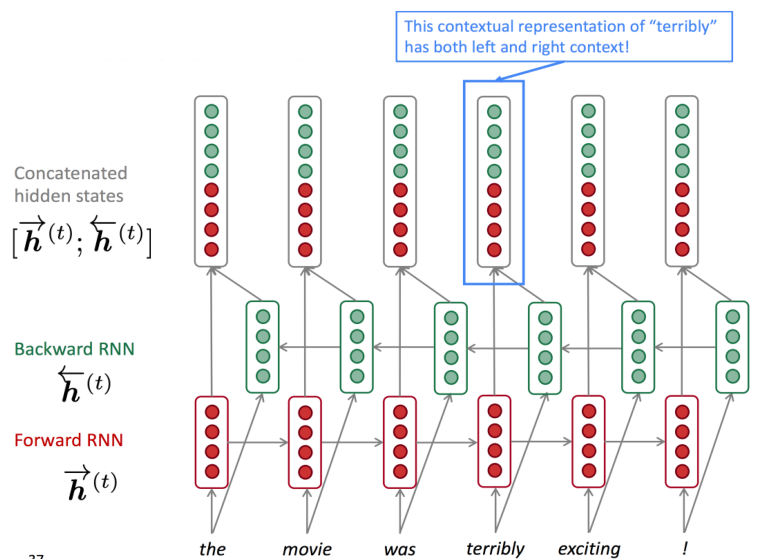
이러한 관점에서 개발된 RNN의 새로운 구조가 bidirectional RNN이다.
이는 forward RNN과 backward RNN 두개를 따로 두고, 최종적인 hidden state는 이 두 RNN에서 생성된 hidden state를 합친 값이 된다.
Deep RNN
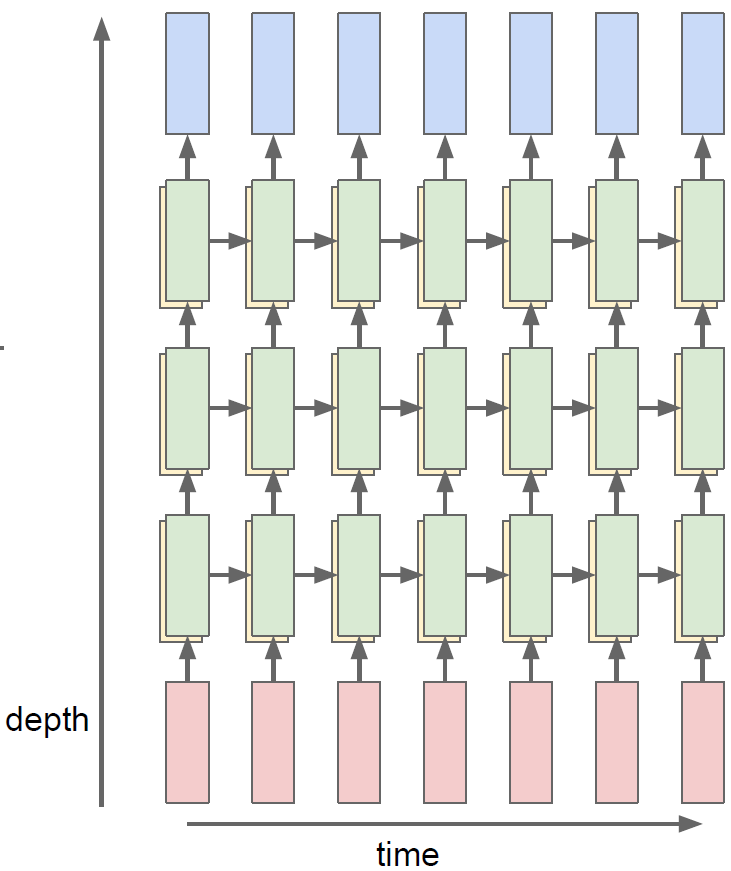
RNN을 여러 layer로 만들어 deep한 RNN 모델을 만들 수도 있다. 이를 deep RNN이라고 하며, 이를 통해 모델이 더욱 복잡한 표현을 학습할 수 있게 된다.
Deep RNN의 형태는 여러가지가 있는데, hidden state layer의 수를 늘리거나, 하나의 hidden state layer에 두 개 이상의 hidden state를 두는 방법 등이 있다.
RNN은 model이 조금만 deep해져도 time step을 모두 고려해야만 하는 이유로 학습이 쉽게 이루어지지 않을 수 있다 (BPTT 참조).
따라서, model이 많이 deep해지는 경우 skip-connection 또는 dense-connection과 같은 기법을 적용해서 학습이 원활이 이루어지도록 모델을 설계하는 것이 중요하다.