Optimization vs Learning

Pure Optimization vs Machine Learning Training?

• The goal of pure optimization is very clear: to find the optimum!
  • Step 1. Represent the problem as a mathematical formulation (as much as possible).
  • Step 2: Find the (possibly) optimum solution.
• On the other hand, in machine learning training, the real optimum and the goal of the training algorithm are similar but not the same.
  • The optimal parameter in learning is not mathematically optimal. (To prevent overfitting)

How Learning Differs from Pure Optimization

In machine learning, the goal is to optimize the performance measure that is evaluated on the test set, not the training set. The test set is unknown during training, making it intractable.

• Fundamentally, training aims to minimize the expectation of the cost function over the (generating) distribution of data.

\[J^*(\theta) = \mathbb{E}_{(x,y) \sim p_{\text{data}}} \mathcal{L}(y, f(x; \theta))\]

That is, sample/data with a low generating probability have less impact on the results even if the error is large. (probabilistic optimization)

• Since the distribution of data is unknown, we use the empirical risk, which is an estimate of the expectation based on the training dataset.

\[J(\theta) = \mathbb{E}_{(x,y) \sim \hat{p}_{\text{data}}} \mathcal{L}(y, f(x; \theta)) = \frac{1}{N} \sum_{i=1}^N \mathcal{L}(y_i, f(x_i; \theta))\]

• Therefore, we need to solve the minimization problem to minimize the empirical risk. However, as mentioned earlier, the minimum of this empirical risk is not necessarily optimum in terms of test set performance. Hence, to prevent overfitting, a regularization term (shown as $\lambda\Omega(\theta)$ in the equation below) is added to the objective function.

\[\min_{\theta} \mathbb{E}_{(x,y) \sim \hat{p}_{\text{data}}} \mathcal{L}(y, f(x; \theta)) + \lambda \Omega(\theta) = \frac{1}{N} \sum_{i=1}^N \mathcal{L}(y_i, f(x_i; \theta)) + \lambda \Omega(\theta)\]

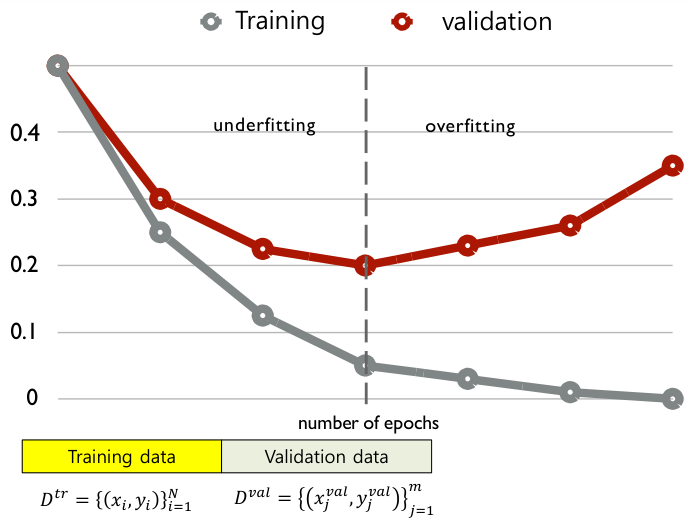
Early Stopping

Since we cannnot know the test set performance in advance, we stop training when the validation error reaches its minimum, in order to predict the performance.

This strategy of stopping training at the point where overfitting begins is called early stopping.