Nyquist Sampling Theory

Posted Apr 1, 2024

3 min read

Introduction

Image에서의 Frequency

물리학에서 frequency는 ‘1초 동안의 주기적 변화의 횟수’ = 1/period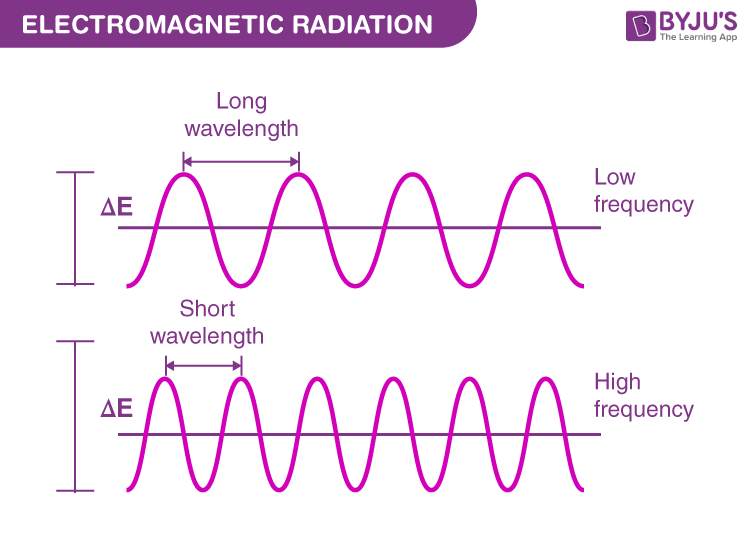

그러나 image에서의 frequency는 ‘공간적으로 패턴이나 특징이 반복되는 정도’를 의미하며, pixel 간의 밝기 변화를 기반으로 계산됨.

High frequency는 밝기가 급격하게 변하는 영역(예: 선명한 가장자리)을 의미하고, low frequency는 밝기 변화가 상대적으로 완만한 영역(예: 부드러운 배경)을 의미

Sampling and Quantization

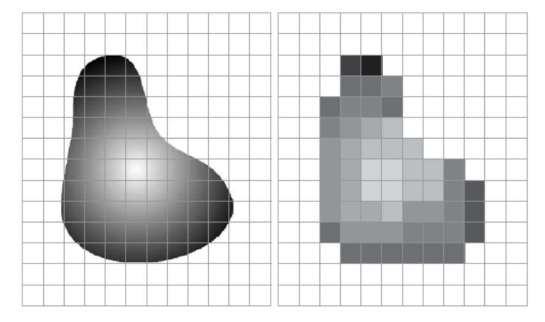
Sampling: 연속적인 이미지(아날로그 이미지)를 이산적인 픽셀 값으로 변환하는 과정

Lower samples rate (resolution) → image가 block처럼 보임 (Blockiness)

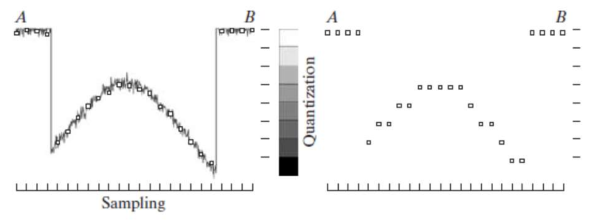
Quantization: 샘플링된 값(픽셀의 색상값)을 특정 범위의 유한한 숫자로 제한하는 과정

Lower # of quantization levels → 경계와 detail이 사라지고, 특정 영역에서 색이 모두 white로 바뀌는 saturation 현상이 발생

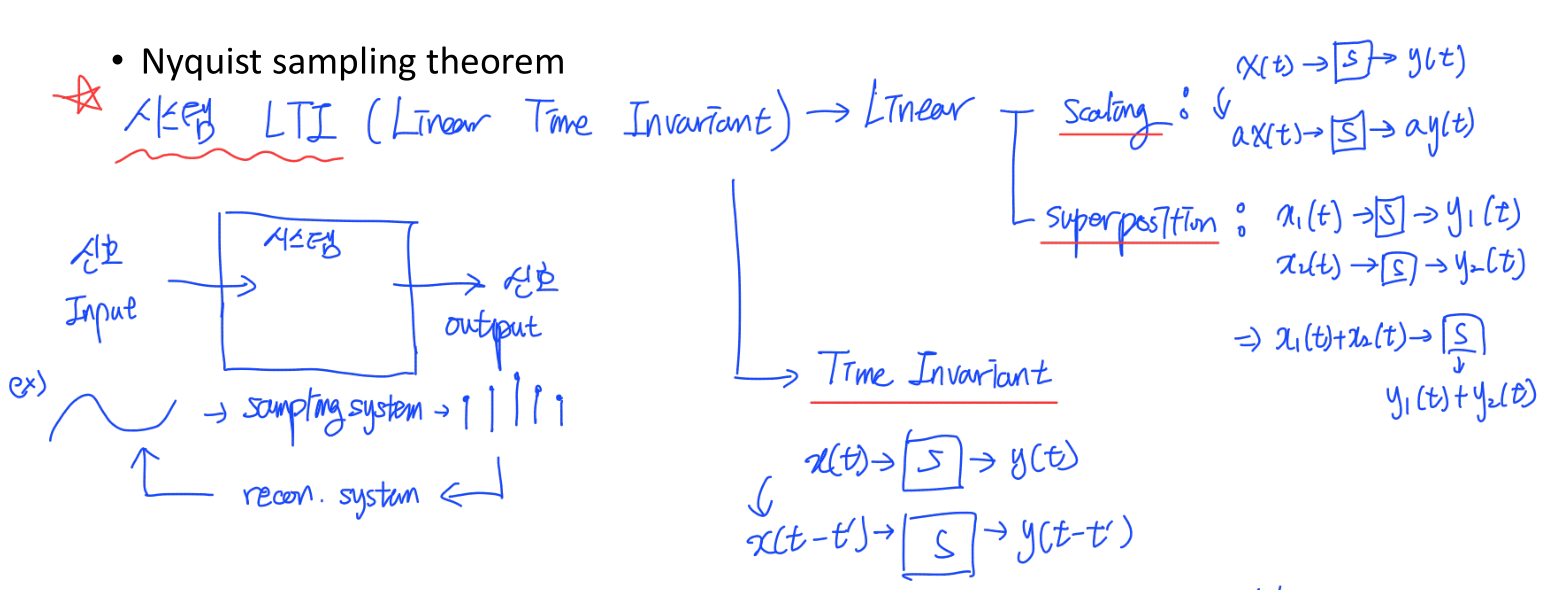
Linear Time Invariant(LTI) System

Linear -> Scaling, Superposition
Time Invariant

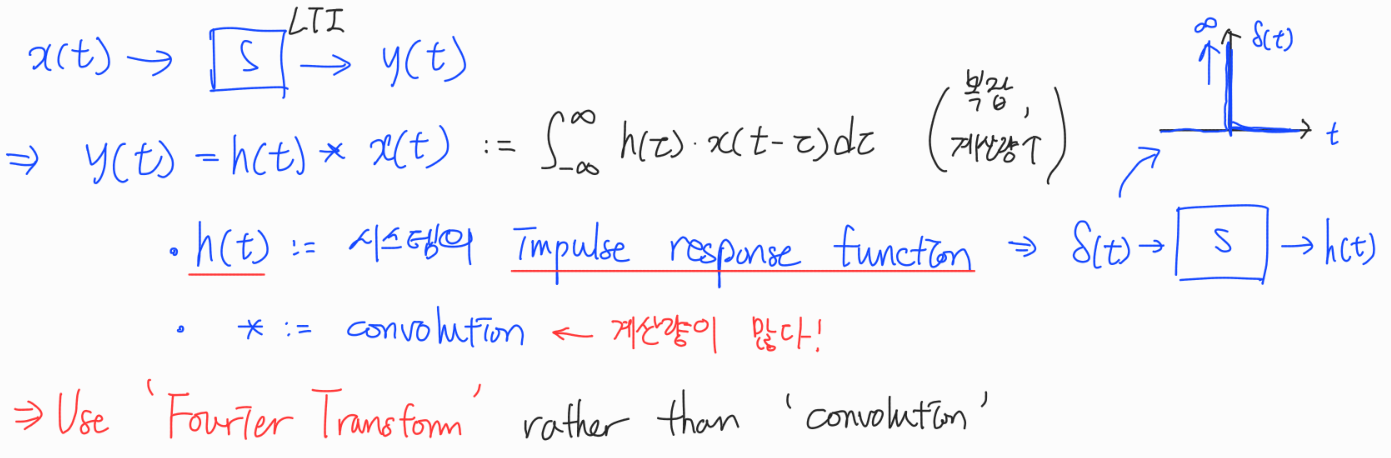
Impulse response function
Convolution

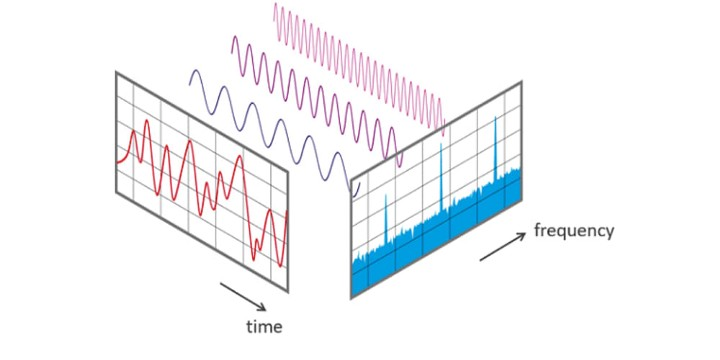
Fourier Transform

Fourier Transform(FT)은 주어진 신호를 다양한 frequency를 가지는 주기 함수들(sin, cos)의 합으로 나타내는 것이다. 즉, time domain을 frequency domain으로 바꿔준다.

\[X(f) = \int_{-\infty}^{\infty} x(t) e^{-j 2\pi ft} dt\]

$x(t)$의 FT 변환 결과인 $X(f)$의 복소수 값의 크기는 주파수 성분의 진폭을 뜻하고, 각도는 주파수 성분의 위상을 뜻한다.

Properties of Fourier Transform

참고 공식
$e^{jwt} = \cos wt + j \sin wt$
$\cos wt = \frac{1}{2}(e^{jwt}+e^{-jwt})$
$\sin wt = \frac{1}{2j}(e^{jwt}-e^{-jwt})$

$w=2\pi f$라고 하자. 그러면, $x(t)$의 FT는 다음과 같다.

\[\mathscr{F}(x(t)) = X(w) = \int_{-\infty}^{\infty} x(t) e^{-jwt} dt\]

Inverse FT는 역으로 frequency domain을 time domain으로 바꿔준다. (synthesize frequencies)
- 동일한 function에 대한 FT와 Inverse FT는 동일하다. (duality)
  \[x(t) = \frac{1}{2\pi}\int_{-\infty}^{\infty} X(w)e^{jwt}dt\]
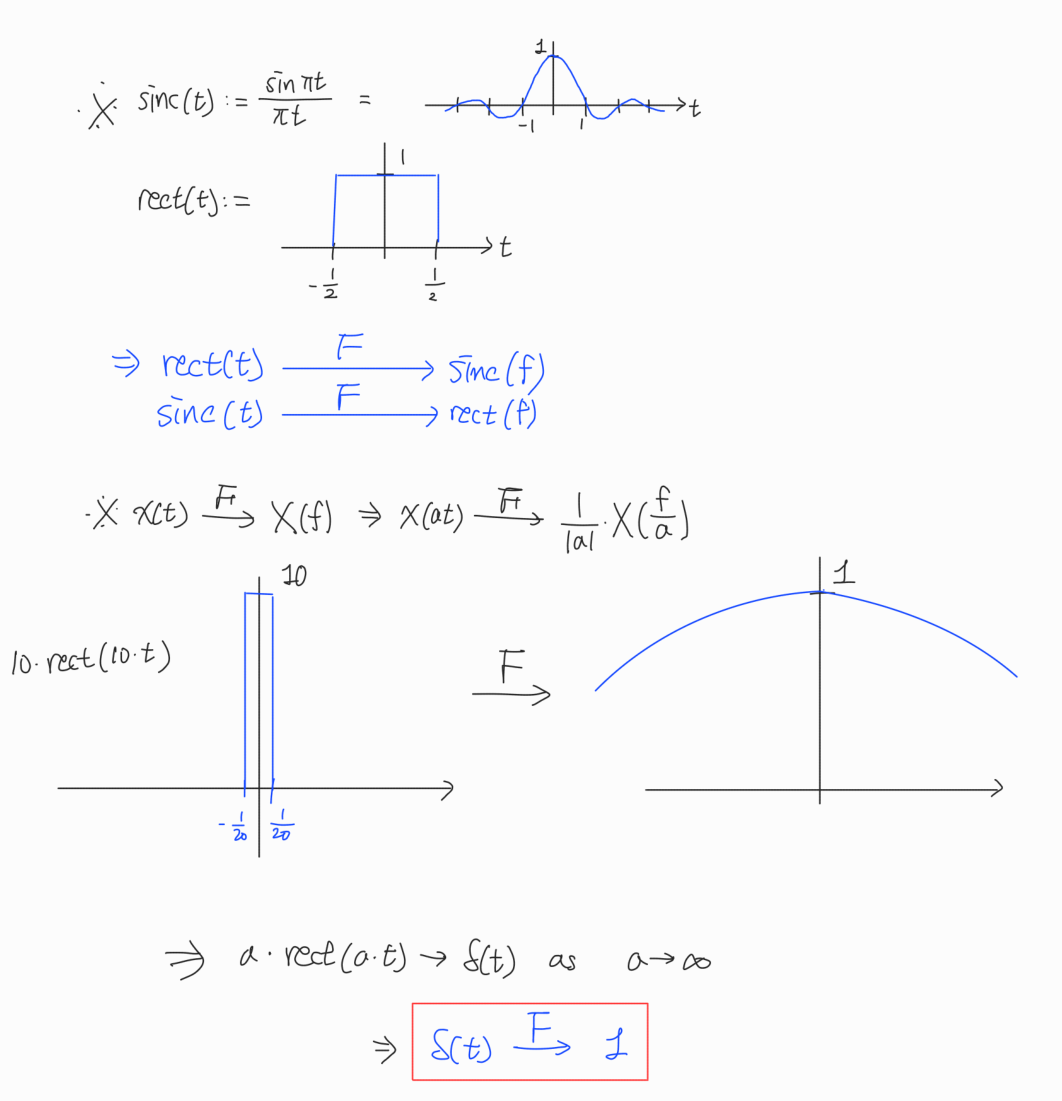
$\delta(t)$의 Fourier transform은 1 이다.
- $\mathscr{F}(\delta(t)) = \int_{-\infty}^{\infty} \delta(t) e^{-jwt} dt = 1\times\int_{-\infty}^{\infty} \delta(t) dt= 1$
$x(t-t_o)$의 Fourier transform은 $X(w)e^{-jwt_0}$ 이다.
- Inverse FT 사용하면 쉽게 확인 가능
- 크기는 동일하나, $t_0$만큼 phase가 shift된다.
Convolution 연산은 Fourier 변환 시, 곱 연산으로 바뀐다.
- $y(t)=x(t)*h(t) \rightarrow \mathscr{F}(y(t))=Y(w)=X(w)\cdot H(w)$
For a constant $a$, $\mathscr{F}(x(at))=\frac{1}{\vert a\vert}X(\frac{w}{a})$.
$\mathscr{F}(x(t)e^{jw_0t})=X(w-w_0)$.
$\mathscr{F}(x(t))\cos w_0t=\frac{1}{2}(X(w-w_0)+X(w+w_0))$
- $\int_{-\infty}^{\infty} x(t)\cos w_0t e^{-jwt} dt = \frac{1}{2}\int_{-\infty}^{\infty} x(t)(e^{jw_0t}+e^{-jw_0t}) e^{-jwt} dt$

적당한 신호에 대해서는 Fourier transform을 빠르게 계산하는 법(FFT)이 개발되어 있다.

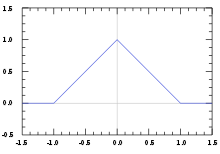
Rect and Sinc Functions

Rect, Sinc, Delta
Triangular

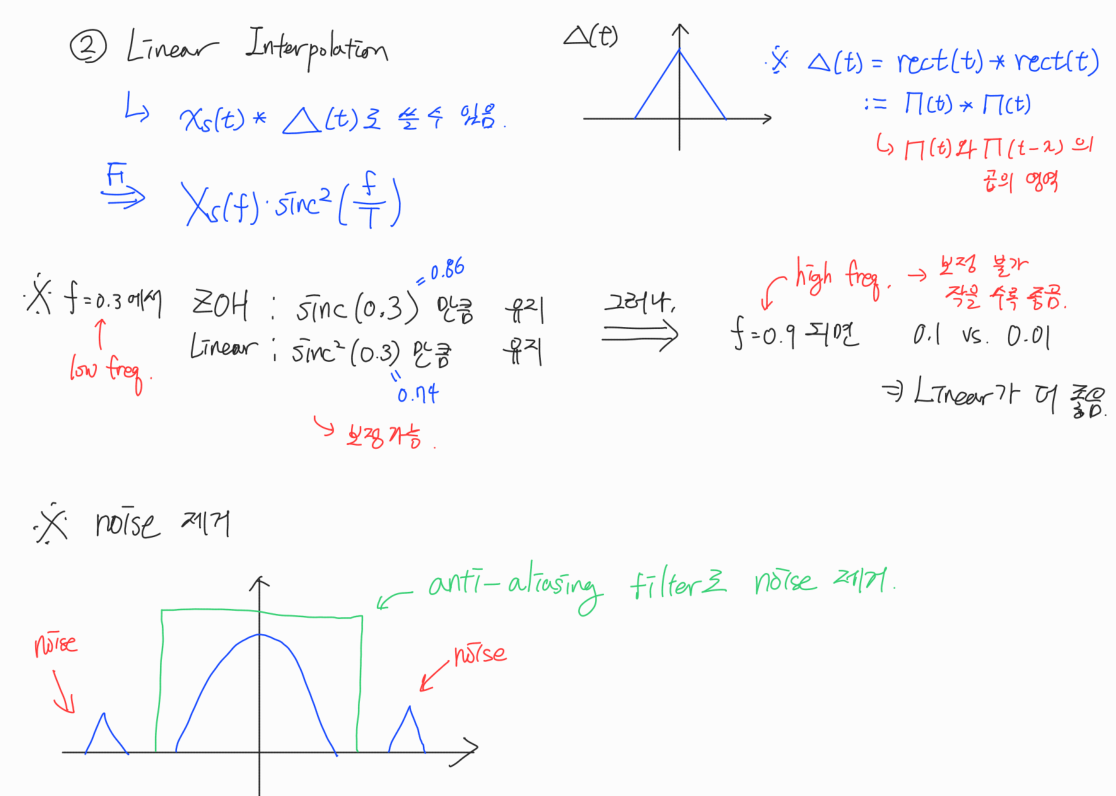
\[tri(t) = rect(t)*rect(t) \Rightarrow \mathscr{F}(tri(t)) = sinc(f)\times sinc(f) = sinc^2(f)\]

역도 성립한다.

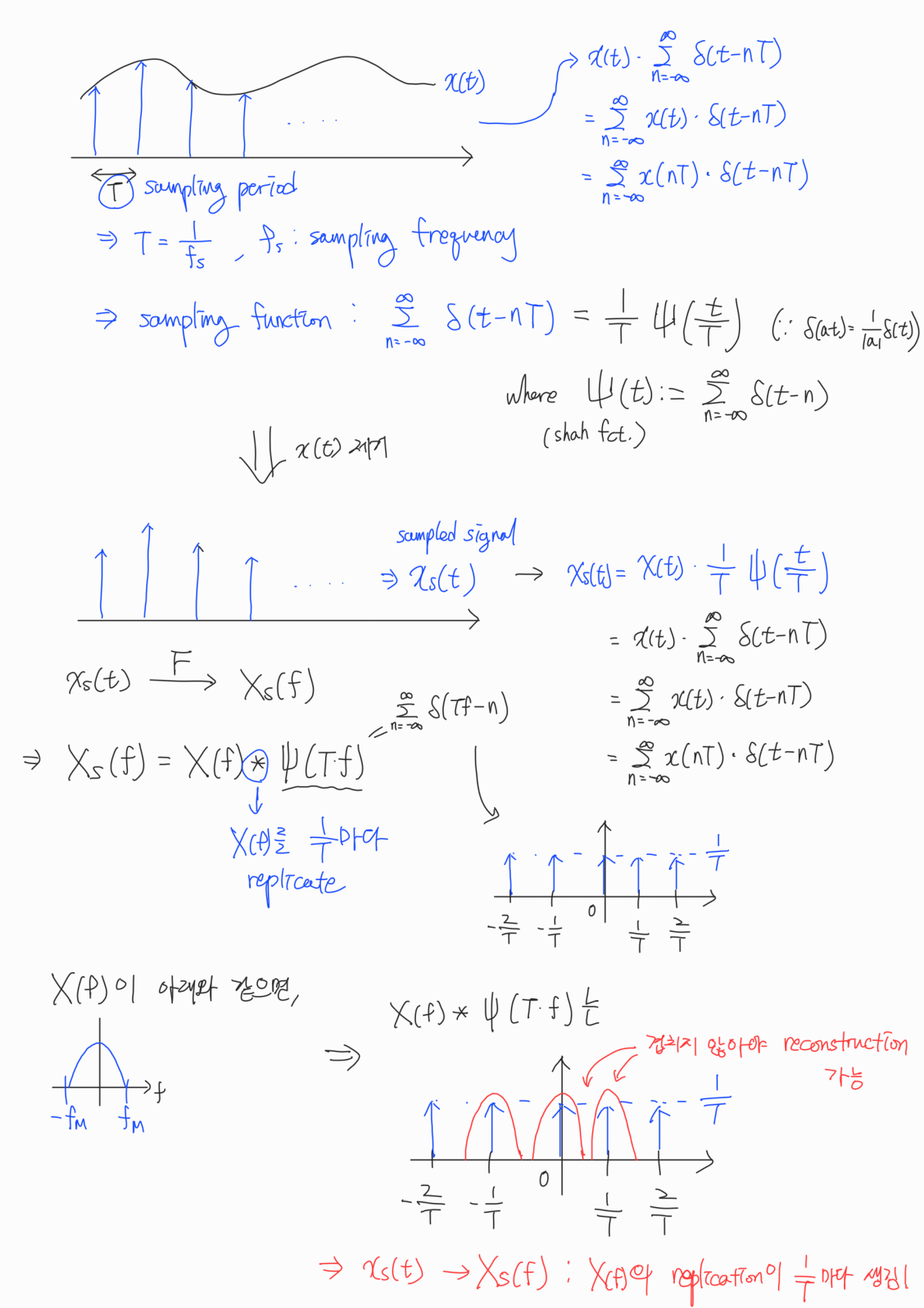
Nyquist Sampling Theory

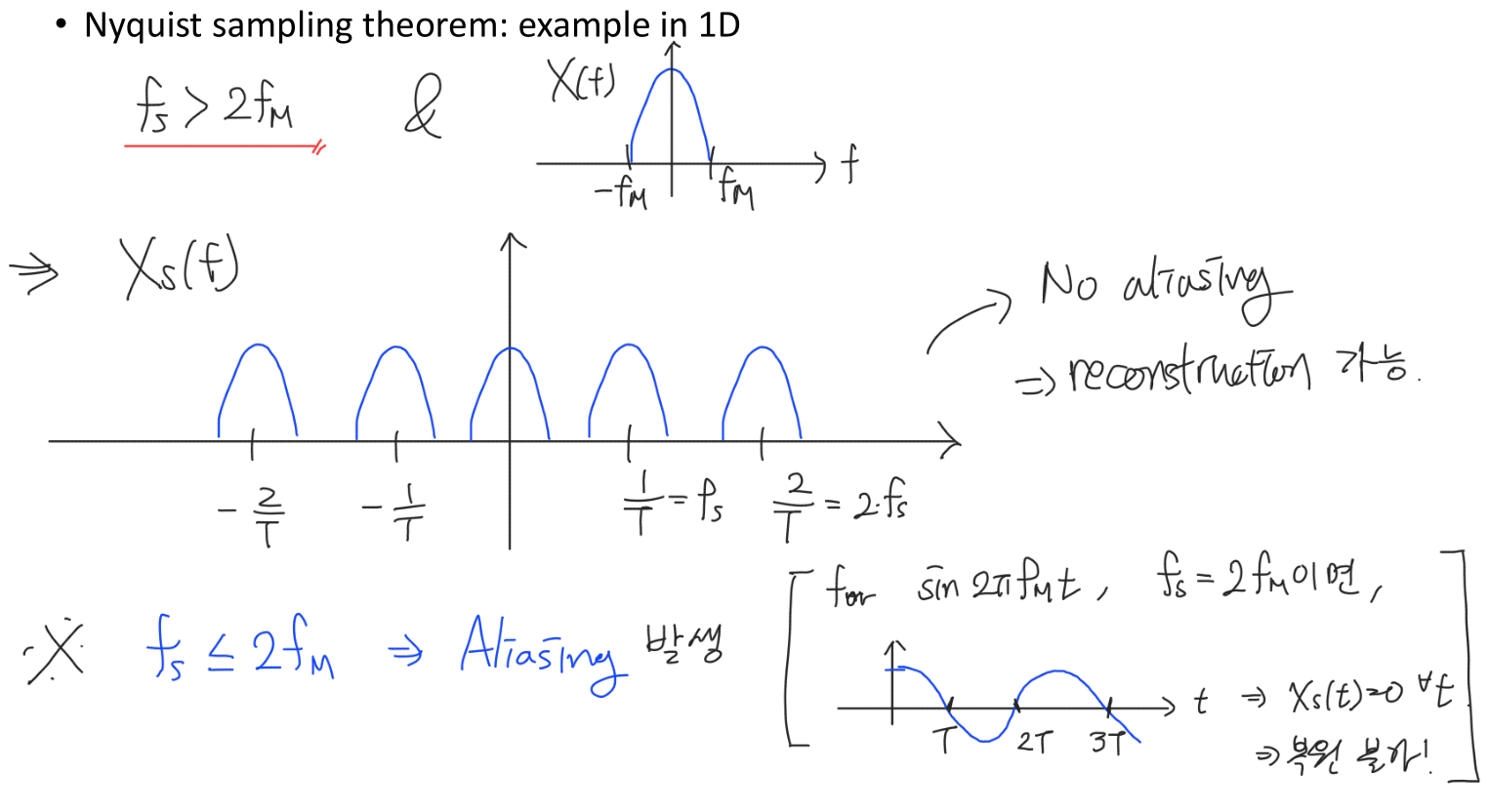
Theorem: Nyquist Sampling

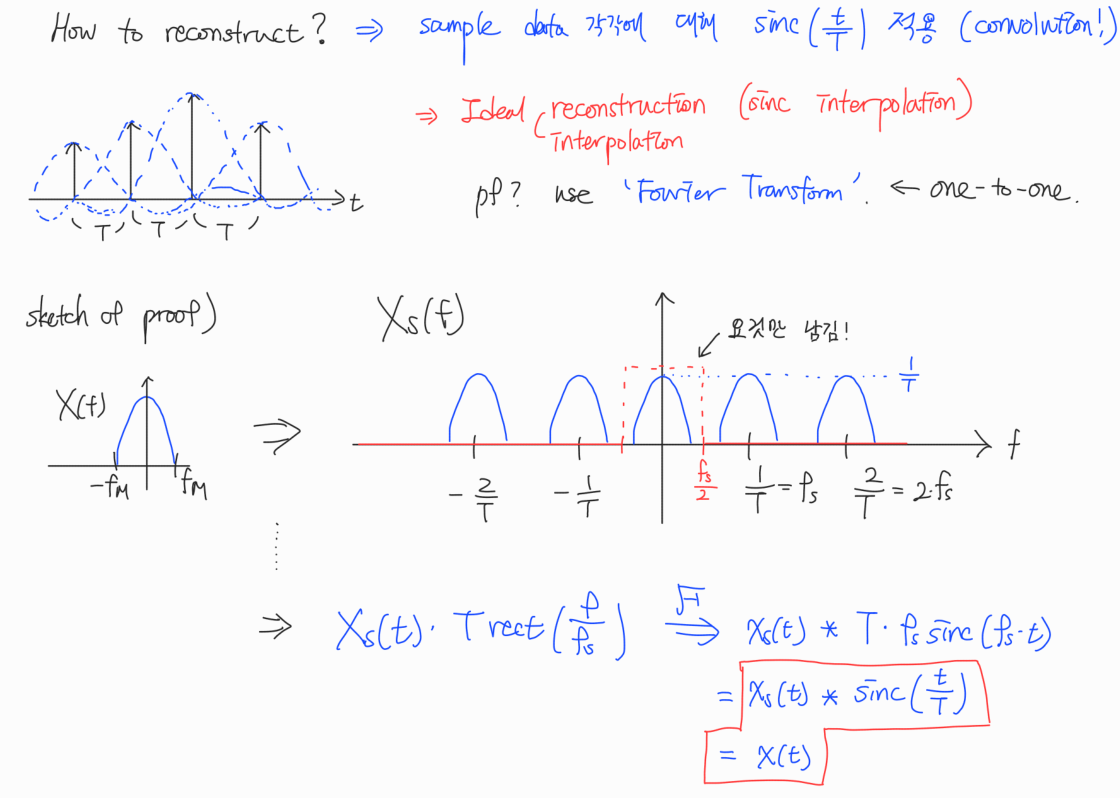
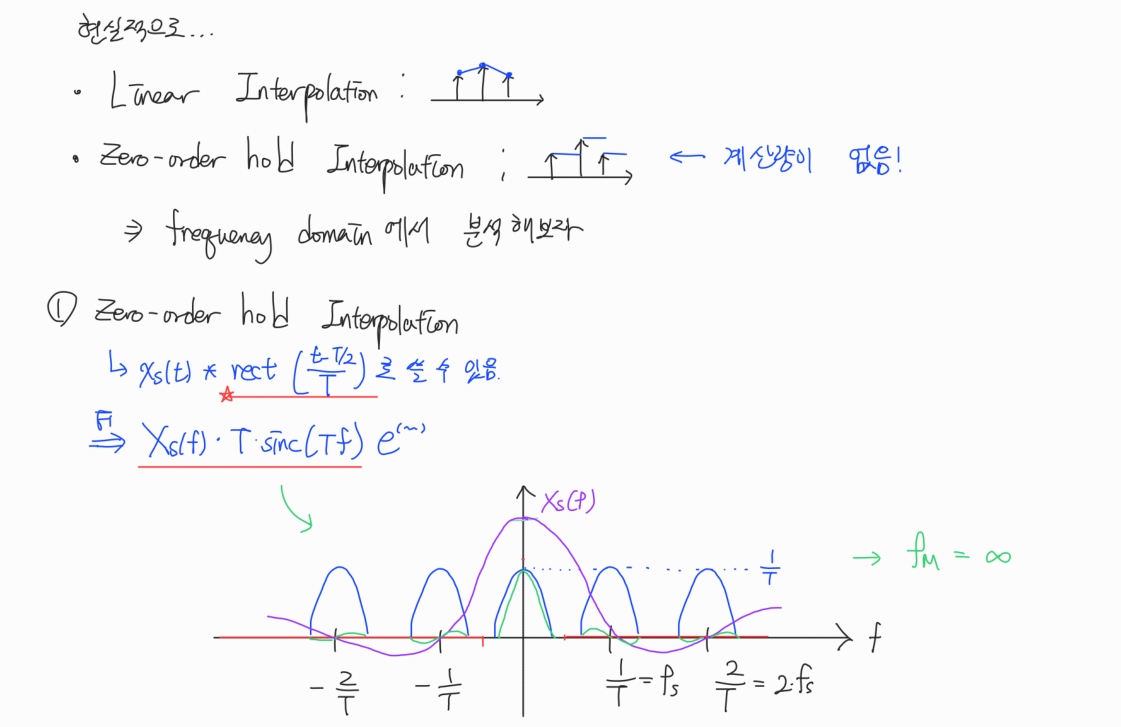
For a band-limited signal, if we sample more than twice the maximum frequency of the signal, we can perfectly reconstruct the original signal from the samples.