Model-free Prediction
Model-Free RL
이전 post ‘Solving MDP’를 통해 우리가 MDP를 알고 있는 경우, DP를 이용한 prediction 및 control이 가능하다는 것을 확인했다. 하지만, 우리가 실제 마주하는 문제들의 경우 MDP에 대해서 알 수 없는 경우가 거의 100%이다. 즉, transition probability와 reward 체계에 대해서 미리 알지못한다는 것이다. 우리는 단지 여러번의 경험을 통해 얻은 episode들로써 이를 추정해내어야 한다.
이러한 문제에 대한 강화학습을 model-free RL이라고 한다. 우선 model-free prediction 방법론에 대해서 다룰 예정으로, 대표적인 알고리즘으로는 Monte-Carlo (MC) policy evaluation과 temporal difference (TD) learning이 있다.
Monte-Carlo Policy Evaluation
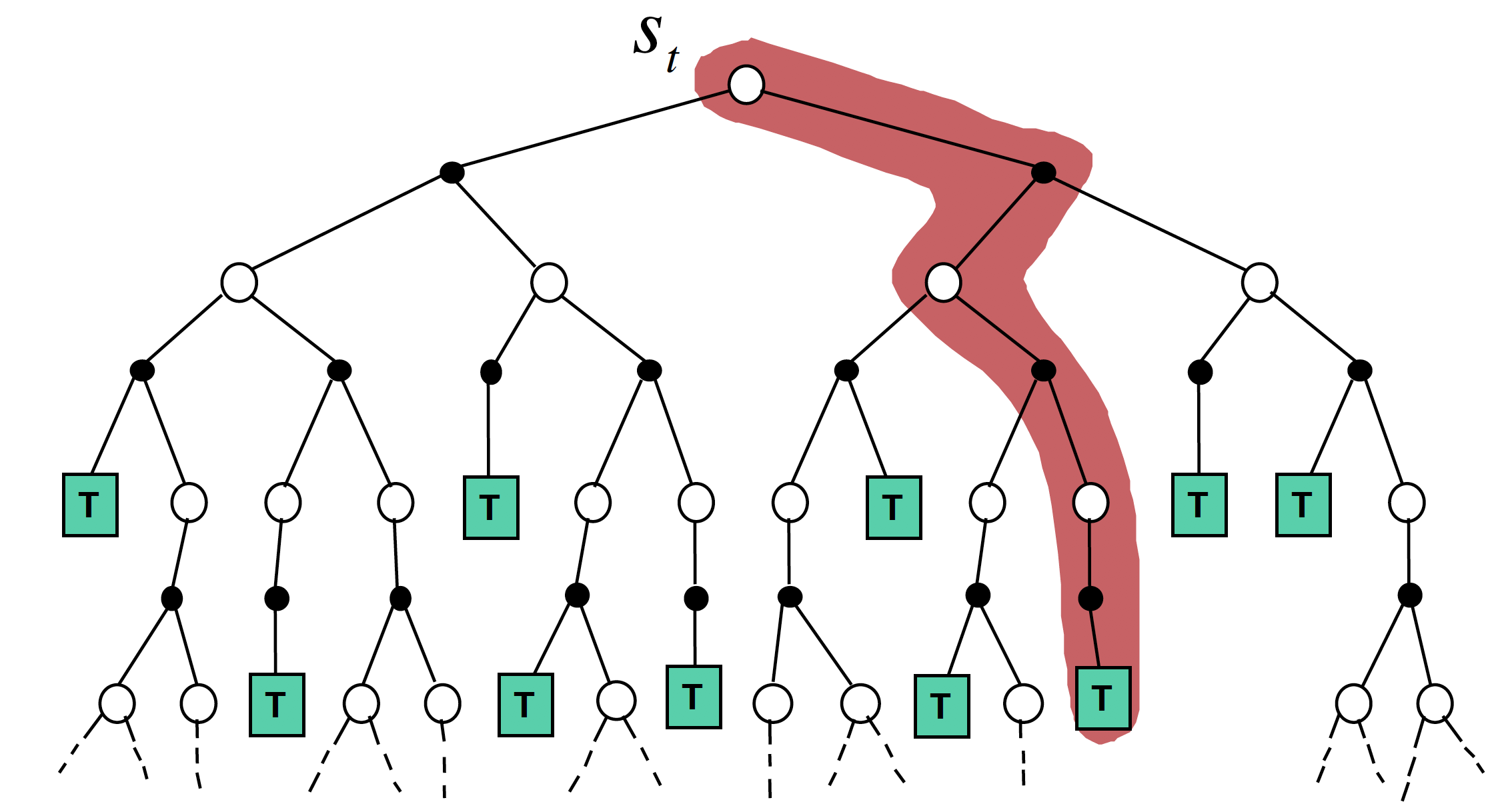
Monte-Carlo (MC) policy evaluation은 model-free prediction 기법으로, 환경과 반복적인 상호작용을 통해 직접 return을 얻어내고, 그 값을 평균내어 value function $V_\pi$를 추정하는 기법이다. Return을 얻기 위해서는 한 episode가 끝나야하기 때문에, value function의 update는 episode가 종료된 이후 이루어진다.
기억을 되살려보면, return과 value function은 각각 다음과 같의 정의되었다.
\[G_t = R_{t+1} + \gamma R_{t+2} + \cdots + \gamma^{T-1} R_T\] \[V_\pi(s) = E_\pi[G_t \mid S_t=s]\]즉, $V_\pi(s)$를 Monte-Carlo 방법으로 추정함에 있어서 return $G_t$에 대한 sample을 이용하는 것이 바로 Monte-Carlo evaluation이다. 어떤 state $s$의 value는 state $s$에서 얻을 수 있는 return의 평균이기에,
\[V(s) = \frac{S(s)}{N(s)}\]- $S(s)$: state $s$ 방문 이후에 얻은 return의 합
- $S(s) \leftarrow S(s) + G_t$
- $N(s)$: state $s$ 방문 횟수
- $N(s) \leftarrow N(s) + 1$
으로 value를 추정할 수 있다.
이 때, update를 하는 방식에 따라, first-visit과 every-visit MC evaluation으로 나눌 수 있다. First-visit MC evaluation은, 특정 state를 처음 방문했을 때만 그 state의 return을 사용하여 value 추정값을 업데이트한다. 반면, Every-visit MC evaluation은 각 state가 episode 내에서 방문될 때마다 그 state의 return을 사용하여 value 추정값을 업데이트한다.
Incremental Monte-Carlo Updates
앞서 설명한 vanilla MC evaluation에서, $V(s)$를 directly update하는 방법이 있다.
\[V(S_t) \leftarrow V(S_t) + \frac{G_t - V(S_t)}{N(S_t)}\]Incremental mean: $\mu_k = \mu_{k-1} + \frac{1}{k}(x_k - \mu_{k-1})$
위 식을 변형하여, learning rate $\alpha$를 붙여 다음과 같이 update하기도 한다. 이를 incremental MC evaluation이라 말한다.
\[V(S_t) \leftarrow V(S_t) + \alpha (G_t - V(S_t))\]Temporal Difference Learning
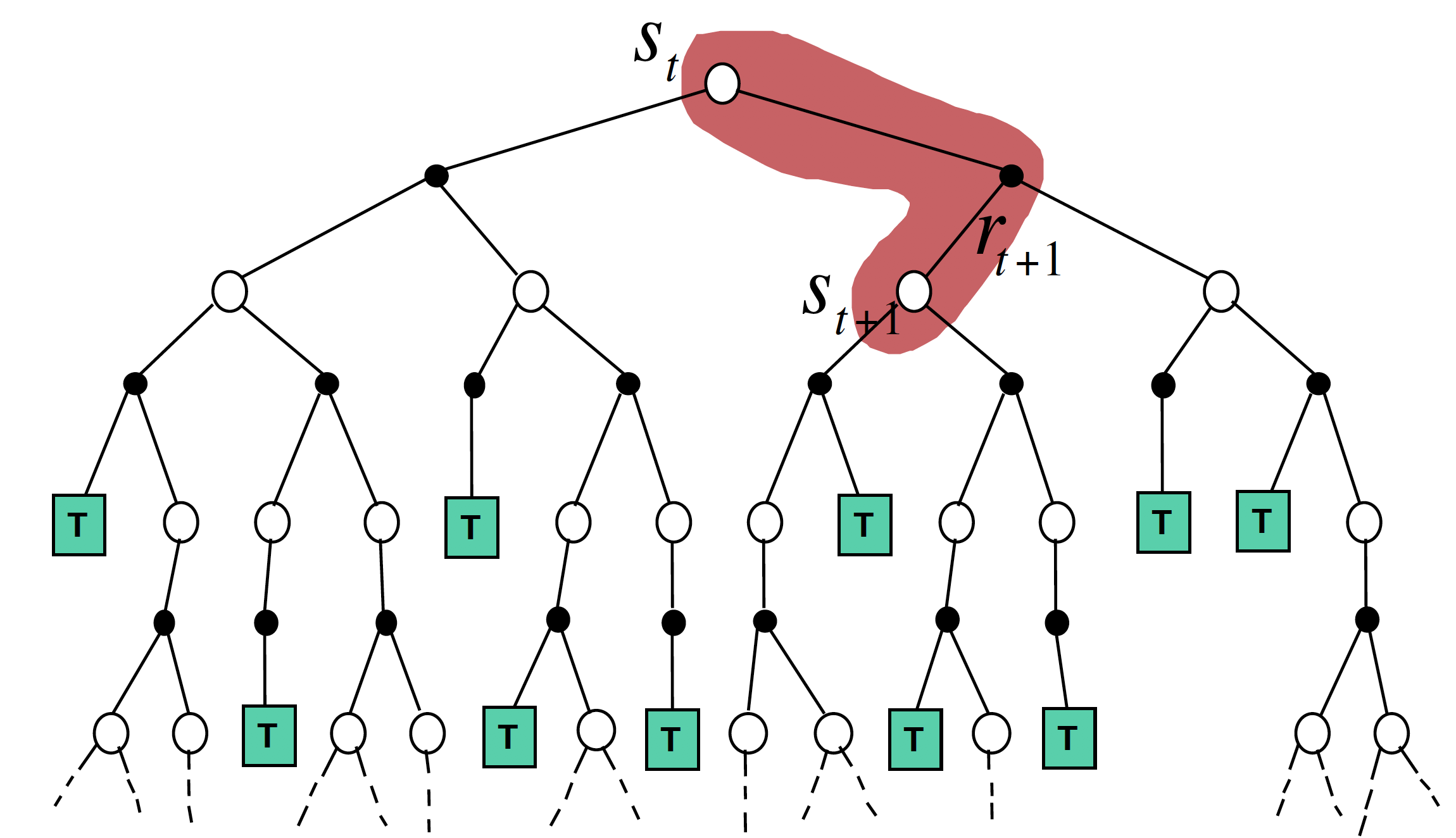
Temporal difference (TD) learning은 MC evaluation과는 다르게 episode가 끝나지 않은 상태에서 한 단계 또는 몇 단계의 경험을 통해 value function의 update를 진행한다. TD learning은 미래 상태의 정보를 이용하여 현재 상태의 정보를 update하는 방식인 bootstrapping을 사용한다.
미래 상태의 정보 역시 estimate 값이기 때문에, TD learning은 estimate 값을 통해 estimate를 진행한다는 것으로 볼 수 있다.
가장 간단한 TD learning 알고리즘은 한 단계의 경험만으로 update를 진행하는 TD(0) learning 알고리즘으로 one-step TD learning이라고도 한다.
\[V(S_t) \leftarrow V(S_t) + \alpha (R_{t+1} + \gamma V(S_{t+1}) - V(S_t))\]이 때, $R_{t+1} + \gamma V(S_{t+1})$를 TD target, $R_{t+1} + \gamma V(S_{t+1}) - V(S_t)$를 TD error라고 한다.
TD(n) learning
TD(n) learning은 n개의 step에 대한 경험을 통해 value function을 update하는 로직이다.
For $n = 1,2, \ldots, \infty,$
\[\begin{aligned} n = 1& \quad (\text{TD}) \quad &G^{(1)}_t &= R_{t+1} + \gamma V(S_{t+1}) \\ n = 2& \quad &G^{(2)}_t &= R_{t+1} + \gamma R_{t+2} + \gamma^2 V(S_{t+2}) \\ \vdots \\ n = \infty& \quad (\text{MC}) \quad &G^{(\infty)}_t &= R_{t+1} + \gamma R_{t+2} + \gamma^{T-1} R_T \\ \end{aligned}\]일 때, TD(n) learning 알고리즘은 다음과 같다.
\[V(S_t) \leftarrow V(S_t) + \alpha \left( G^{(n)}_t - V(S_t) \right)\]n이 커질수록 TD(n) learning은 MC evaluation과 유사하게 진행된다.
TD($\lambda$) learning
TD($\lambda$) learning은 모든 step에 대한 경험에 대해서 decaying factor $\lambda \in [0,1]$을 이용한 weighted sum을 통해 value function update를 진행하는 알고리즘이다.
TD($\lambda$) learning 알고리즘은 다음과 같다.
For $G^\lambda_t = (1 - \lambda) \sum_{n=1}^\infty \lambda^{n-1} G^{(n)}_t$,
\[V(S_t) \leftarrow V(S_t) + \alpha \left( G^\lambda_t - V(S_t) \right)\]$\lambda = 0$이면, TD($\lambda$) = TD(0) 이고, $\lambda = 1$이면, TD($\lambda$) = TD(1) = MC 이다.
MC vs. TD
Rates of Convergence
MC와 TD는 모두 prediction 방법이지만, update가 가능한 시점에 있어서 큰 차이가 있다. TD learning은 각 state에 대한 value function을 episode를 진행하면서 바로 update를 할 수 있기 때문에 상대적으로 MC에 비해 학습 속도가 빠르다.
TD learning은 continuing 환경, 즉 끝이 따로 없는 환경에서도 학습을 진행할 수 있다.
Bias/Variance Trade-off
Return $G_t$는 $V_\pi (S_t)$의 unbiased estimate이다. 즉, 실제 return 값을 아주 많이 모아 estimation을 진행하는 MC evaluation은 시간은 오래걸리더라도 보다 정확한 값을 갖게 된다.
반면에, TD의 경우, return에 대한 estimate인 TD target $R_{t+1} + \gamma V(S_{t+1})$을 사용한다. 즉, TD target은 $V_\pi (S_t)$의 biased estimate이 된다. 하지만, TD traget은 한 개 또는 몇 개만의 transition으로 계산이 되기 때문에, 계산을 위해 훨씬 더 많은 transition이 필요한 실제 return 값에 비해 더 낮은 variance를 갖는다.
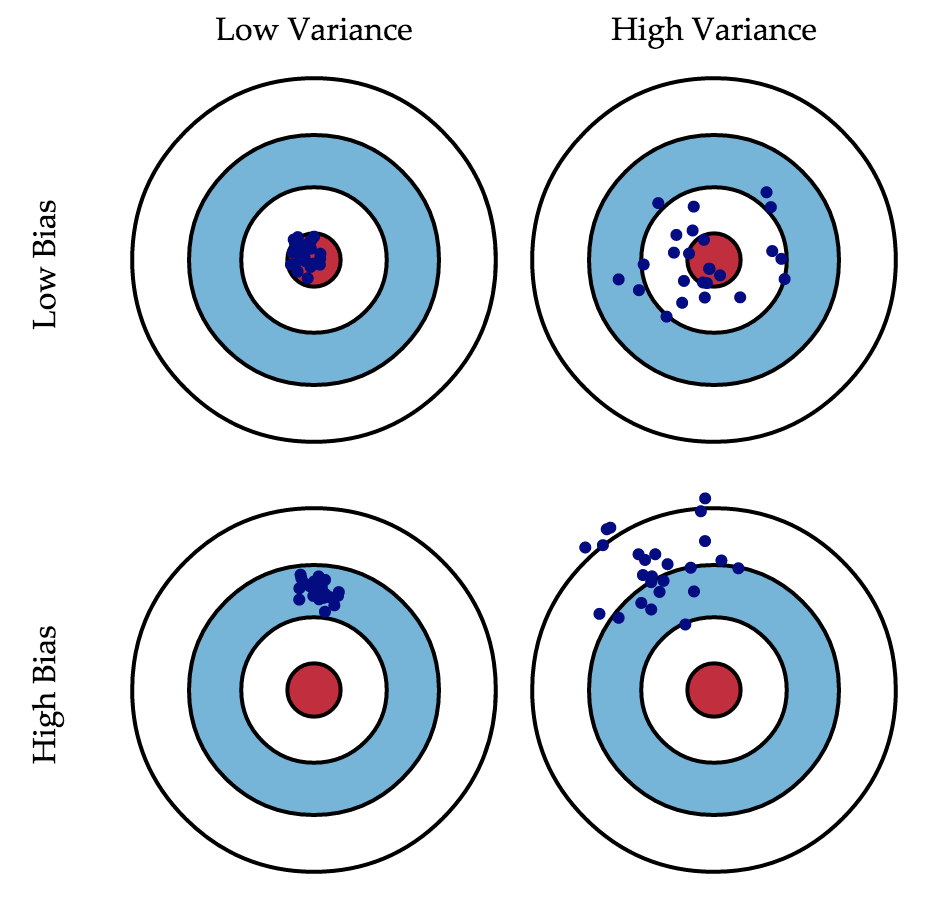
즉, MC는 TD에 비해 더 높은 variance를 갖지만, bias는 없다. 반대로, TD는 MC에 비해 더 낮은 variance를 갖지만, 어느정도의 bias를 갖는다.
시간과 계산 비용 측면에서, 일반적으로는 TD learning, 그 중에서도 TD(0) learning이 선호된다. 다만, TD learning의 결과는 initialization에 따라 결과가 크게 달라질 수 있음을 주의하자.
Markov Environment
TD는 기본적으로 Markov property를 가정하고 알고리즘이 구현되었다. 따라서, Markov 환경에서 좀 더 효과적으로 동작한다.
반면, MC의 경우 law of large number에 의한 estimate을 사용하기 때문에 Markov property가 없는 non-Markov 환경에서도 잘 동작한다.