Model-free Control
Model-free control이란 환경이 주어져 있지 않거나, 또는 환경을 알 수 있으나 다루기에 너무 큰 상황(예. Robot walking 등)에서 optimal policy를 찾기 위한 방법을 말한다.
Model-free Policy Improvement
Model-free policy improvement 역시 현재 상태에서 얻어낸 value function을 maximize하는 action을 선택하는 것을 통해 얻어낼 수 있다. 이렇게 얻은 greedy policy $\pi’$은 다음과 같다.
\[\begin{aligned} \pi'(s) &= \arg\max_{a \in A} \left( R^a_s + \gamma \sum_{s' \in S} P_{ss'}^a V_{\pi}(s') \right)\\ &= \arg\max\limits_{a \in \mathcal{A}} Q_\pi(s,a) \end{aligned}\]다만 model-free 환경에서는 transition probability와 reward를 미리 알 수 없기 때문에, action-value function $Q(s,a)$을 사용해야만 한다.
즉, model-free prediction 방법론을 $Q(s,a)$에 대해 적용하는 것이 필요하다.
$\epsilon$-greedy Policy Improvement
하지만, $Q(s,a)$를 이용한 greedy policy는 우리가 충분한 action-state pair에 대해 탐색하지 않으면 제대로 동작하지 않을 가능성이 높다. 이러한 문제를 개선하기 위해 등장한 것이 바로 $\epsilon$-greedy policy improvement이다.
일반적인 $\epsilon$-greedy policy improvement에서는 $1-\epsilon$의 확률로 greedy action을, $\epsilon$의 확률로 임의의 행동을 선택한다. 이를 수식으로 표현하면 다음과 같다.
\[\pi(a|s) = \begin{cases} \frac{\epsilon}{m} + 1 - \epsilon & \text{for } a^* = \arg\max\limits_{a \in A} Q(s, a) \\ \frac{\epsilon}{m} & \text{for other } a \end{cases}\]Model-free Control
앞서 언급했듯이, model-free control의 경우 $Q(s,a)$에 대해 evaluation하는 방법이 필요하다. 일전에 설명한 Monte-Carlo (MC) evaluation 또는 temporal difference (TD) learning을 사용할 수 있다.
하지만 일반적으로 MC evaluation에 비해 TD learning 방법이 더 널리 사용되므로 여기서는 TD learning을 이용한 evaluation에 대해서만 설명하고자 한다. TD learning을 이용한 model-free evaluation 방법은 SARSA와 Q-learning이 있다.
On-policy vs. Off-policy
SARSA와 Q-learning은 유사한 알고리즘이나, 각각 on-policy와 off-policy 알고리즘이라는 차이가 존재한다.
Agent가 action을 선택할 때 사용되는 policy와 agent가 value function을 update할 때 사용되는 policy가 같은 경우 on-policy 알고리즘, 다른 경우 off-policy 알고리즘이라고 한다.
On-policy 알고리즘의 경우 학습에 사용되는 policy와 value function을 평가하는데 사용되는 policy가 동일하므로 안정적으로 학습이 가능하다. 하지만, 현재 action을 선택하는 policy로 얻은 데이터만 사용할 수 있으므로 데이터 효율성이 떨어지고, exploration과 exploitation 사이의 균형을 맞추기가 어렵다는 단점이 있다.
반면, Off-policy 알고리즘은 exploration을 더 적극적으로 수행할 수 있기 때문에 더 빠른 수렴이 가능하다. 하지만, 학습에 사용되는 policy와 value function을 평가하는데 사용되는 policy가 다르기에 학습이 불안정할 수 있다.
SARSA
SARSA는 대표적인 on-policy 알고리즘으로 다음과 같이 동작한다.
- 모든 $s, a$에 대해서 $Q(s,a)$를 초기화한다.
- 현재 state $S$에서 policy $\pi$를 기반으로 action $A$를 선택한다.
- Action $A$를 수행하고, 새로운 state $S’$과 reward $R$을 얻는다.
- 새로운 state $S’$에서 policy $\pi$를 기반으로 action $A’$를 선택한다.
다음 식으로 $(S,A)$에서의 action-value $Q(S,A)$를 update한다.
\[Q(S,A) \leftarrow Q(S,A) + \alpha(R + \gamma Q(S',A') - Q(S,A))\]- $S\leftarrow S’$, $A\leftarrow A’$. 이후, 2번으로 돌아간다.
SARSA는 state-action-reward-state-action 각각의 앞글자를 따 정해진 이름이다.
SARSA는 GLIE를 만족하는 policy $\pi$와 Robbins-Monro sequence에 해당하는 step-size $\alpha$에 대해 optimal로 수렴한다는 것이 알려져 있다.
- GLIE: Greedy in the Limit with Infinite Exploration, 모든 state-action pair가 무수히 많이 explored되는 경우 greedy policy로 수렴하는 (in probability) 성질.
- Robbins-Monro sequence: $\sum_{t=1}^\infty \alpha_t = \infty$ and $\sum_{t=1}^\infty \alpha_t^2 = 1$
Q-learning
Q-learning는 대표적인 off-policy 알고리즘이다.
Off-policy 알고리즘에서는 두 개의 서로 다른 policy를 사용한다.
Agent의 action-value를 update할 때 사용되는 다음 시점의 $Q(S_{t+1},A’)$ 중 $A’$을 결정하는 policy: target policy $\pi$ ($A’ \sim \pi(\cdot \mid S_t)$)
\[Q(S_t,A_t) \leftarrow Q(S_t,A_t) + \alpha(R_{t+1} + \gamma Q(S_{t+1},A') - Q(S_t,A_t))\]Agent의 실제 action 결정하는 policy: behavior policy $\mu$ ($A_{t+1} \sim \mu(\cdot \mid S_t)$)
Q-learning에서는 target policy로 greedy policy ($\pi(S_{t+1}) = \arg\max\limits_{a’}Q(S_{t+1}, a’)$를, behavior policy로 $\epsilon$-greedy policy를 사용한다. 즉, Q-learning은 다음과 같이 동작한다.
- 모든 $s, a$에 대해서 $Q(s,a)$를 초기화한다.
- 현재 state $S$에서 $\epsilon$-greedy policy를 기반으로 action $A$를 선택한다.
- Action $A$를 수행하고, 새로운 state $S’$과 reward $R$을 얻는다.
다음 식으로 $(S,A)$에서의 action-value $Q(S,A)$를 update한다.
\[Q(S,A) \leftarrow Q(S,A) + \alpha(R + \gamma \max_{a'} Q(S',a') - Q(S,A))\]- $S\leftarrow S’$. 이후, 2번으로 돌아간다.
Q-learning 역시 SARSA와 마찬가지로 optimal로 수렴한다는 것이 알려져 있다.
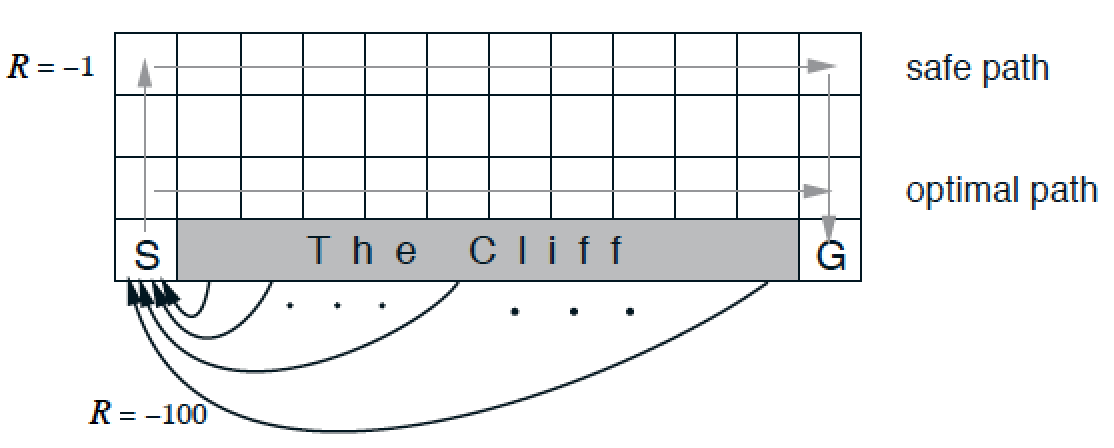
Cliff Walking Example
두 알고리즘의 학습 결과의 차이를 극명하게 보여주는 가장 좋은 예시가 바로 cliff walking problem이다.
이는 아래 그림과 같은 환경에서 S에서 출발해 G로 도착하는 것을 학습하는 문제이다.
- Action: up, down, left, right
- Reward = -1 per time-step, -100 in the cliff, $\gamma$ = 0
- $\epsilon$-greedy with $\epsilon$ = 0.1, $\alpha$ = 0.5
- Initialize $Q(S,A)=0$
위 문제를 학습시켜보면, 중간 시점에 체크해보는 경우 일반적으로 SARSA는 safe path(local optimal)로 수렴하고, Q-learning은 optimal path로 수렴하게 된다.
단, 무수히 많은 episode를 거치면서 $\epsilon$이 0에 수렴하면 두 알고리즘 모두 optimal path를 찾는다.
SARSA는 next state에서의 action을 실제로 수행해보고 이를 현재 state의 value에 반영한다. 즉, optimal path로 가다가 한번 cliff로 떨어지는 경우, 이 때의 경험이 현재 state에 반영되어 cliff 쪽으로 가지 않으려는 성향을 띄게 된다.
반면, Q-learning의 경우 next state에서 cliff에 떨어지는 경험은, next state 에서의 action-state value ($Q(S_{t+1}, A_{t+1}$)에만 반영되며, 현재 state의 value에는 반영되지 않는다 (greedy action으로 선택이 되지 않기 때문). 이러한 이유로 Q-learning은 보다 모험적이나 optimal한 path에 가깝게 행동한다.
이렇게 보면, off-policy 알고리즘이 항상 더 좋다고 느껴질 수 있으나, 이는 SARSA와 Q-learning에 한정한 비교이므로 문제와 특성에 따른 적절한 알고리즘 선택이 필요하다는 점을 주의하자.