Model Evaluation Metric

Model evaluation은 당연하게도 무척 중요하다. 특정 application에 적용할 model이라면, 해당 application에서 요구하는 수준의 performance를 낼 수 있는지 미리 확인 할 수 있어야 한다. 또한, model 자체를 optimizing 하는 것에 있어서도 optimal의 기준이 되는 metric이 필요하다.

여기서는 그러한 model evaluation metric에 대해서 소개한다.

Confusion Matrix

Confusion matrix 란 전체 train data에 대해 ground truth와 prediction에 대해서 각각의 결과를 표로 나타낸 것이다.

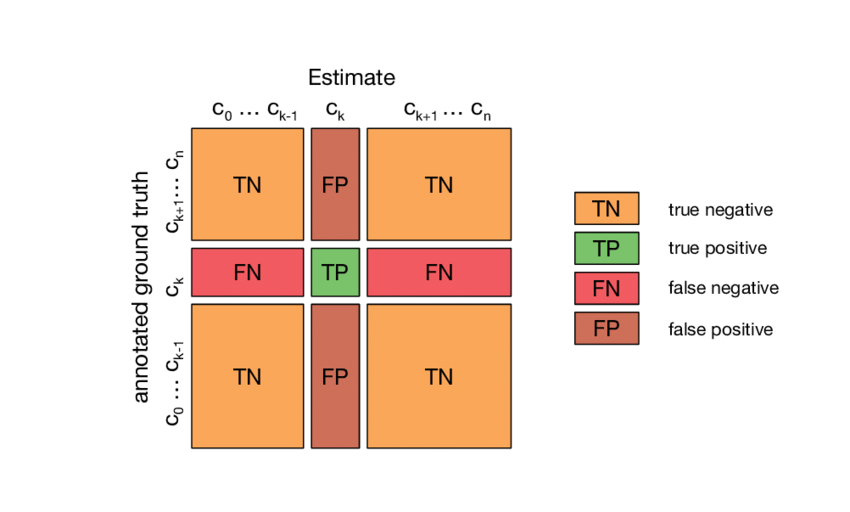
Multiclass classification의 경우 각 class들을 모두 표에 나타낼 수도 있지만, 이를 특정 class를 기준으로 해당 class로의 할당 여부를 기준으로 아래와 같이 binary하게 나타낼 수 있다.

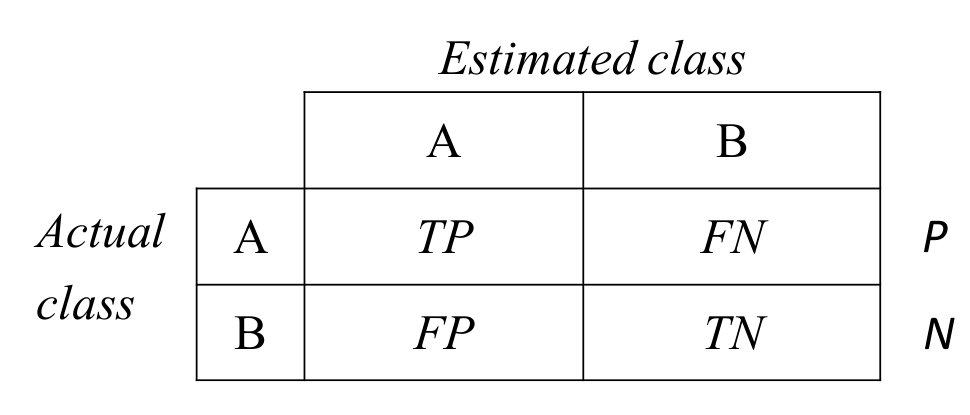
이 경우, 다음과 같이 4개의 영역으로 나눌 수 있다. 쉬운 이해를 위해 기준을 나눈 특정 class에 포함되는 경우를 A, 해당 class에 포함되지 않은 경우를 B라고 하자.

• TP: True Positive
• FN: False Negative
• FP: False Positive
• TN: True Negative

정답을 맞춘 경우 True (아니면 False), 예측이 관심있는 class인 경우 Postive (아니면 Negative)로 기억하자.

Common Metrics

TP, FP 등을 이용하여 계산된 주요 metric은 다음과 같다. 자주 사용되니 기억하자. (P = TP+FN로 실제 A의 개수, N = FP+TN로 실제 B의 개수)

• Accuracy = (TP+TN) / (P+N)
  • 정답률
• Error = (FP+FN) / (P+N)
  • 오답률
• Precision = TP / (TP+FP)
  • A 예측의 정답률
• Recall = TP / P
  • 실제 A의 정답률
• TP Rate, TPR (sensitivity) = TP / P
  • 실제 A의 정답률
• TN Rate (specificity) = TN / N
  • 실제 B의 정답률
• FP Rate, FPR = 1 - TN Rate
  • 실제 B의 오답률

Precision과 Recall은 trade-off 관계이며, TP Rate와 FP Rate 역시 trade-off 관계이다.

여기서 accuracy가 일반적으로 가장 흔하게 사용되는 metric인데, data imbalance가 심한 경우 accuracy의 사용은 주의해야 한다.

만약 실제 data의 5%만이 class A에 속해 있다면, classifier가 항상 class B로 분류하더라도 accuracy는 95%에 달하기 때문에 무조건적인 accuracy에 따른 model 성능 평가는 좋은 방법이 아니다.

F-measure

서로 trade-off 관계에 있는 precision과 recall의 harmonic mean을 metric으로 삼을 수 있다. 이는 F-measure 라고 불리며, best score로 1, worst score로 0을 갖는다.

\[F = \frac{2}{\left(\frac{1}{\text{Precision}} + \frac{1}{\text{Recall}}\right)}\]

ROC Curve

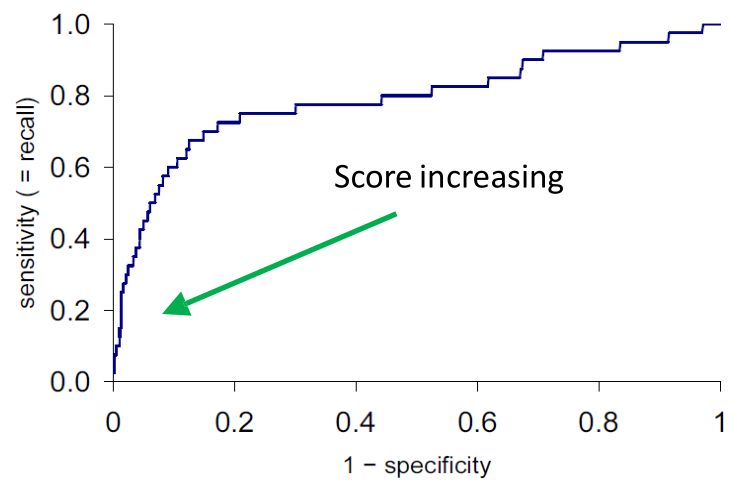
ROC, Receiver-Operating Characteristic, curve는 model의 discrimination threshold의 변화에 따라 FPR과 TPR이 어떻게 바뀌는지를 나타내는 곡선이다.

어떤 model A가 있을 때, A의 ROC curve에 대해서, 해당 model보다 모든 threshold 영역에 대해서 더 높은 ROC curve (같은 FPR 대비 더 높은 TPR)을 가지는 model B가 있다면, B는 A보다 더 좋은 model이라고 말할 수 있다.

하지만 실제적으로 그러한 경우는 거의 없기 때문에 model 간 비교와 선택은 주로 decion making의 영역이 된다.

ROC AUC

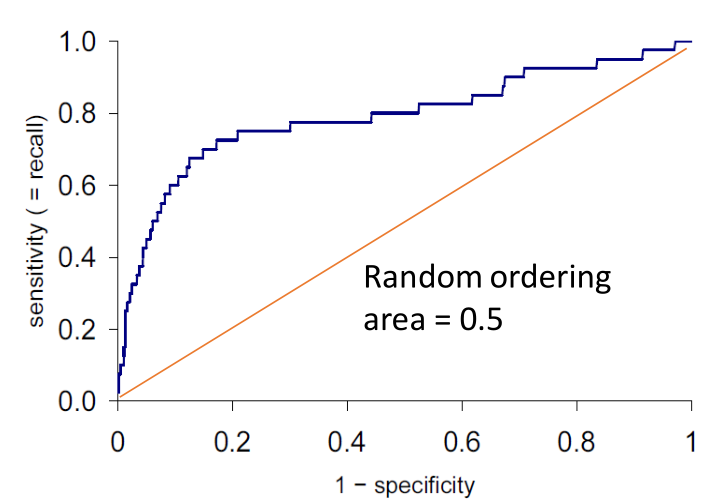
그럼에도 불구하고, model의 성능을 표현하는 한가지 지표를 표현하라고 한다면, ROC curve의 Area Under the Curve(AUC), 즉 ROC AUC 가 그 지표가 될 수 있다.

ROC AUC가 큰 model일 수록 작은 FPR에 대해서 큰 TPR을 가지는 경향을 보인다고 할 수 있기에 더 좋은 model로써 평가받을 확률이 높다.

ROC AUC는 0.5(random classifier)에서 1.0(perfect) 사이의 값을 갖는다.