Markov Decision Process

Markov Process

Markov process란, Markov property를 만족하는 random variable의 sequence로, $\langle S,P \rangle$로 나타낸다.

• State의 집합: $S$

• Transition probability matrix (model): $P: S\times S \rightarrow \mathbb{R}, P_{ss’} = P(S_{t+1} = s’ \mid S_t = s)$

Markov Property

Markov property (MP)란 미래의 state가 현재의 state에만 의존하는 성질을 말한다. 즉, 미래 정보를 예측함에 있어서 모든 과거 정보가 필요한 것이 아니라, 가장 최근의 정보만 있어도 충분할 때, 이는 Markov property를 갖는다고 말한다.

다음 식이 성립하는 sequence에 대해 Markov property를 갖는다고 말한다.

\[P(S_{t+1} = s_{t+1} \mid S_t = s_t, \ldots, S_0 = s_0) = P(S_{t+1} = s_{t+1} \mid S_t = s_t)\]

같은 문제에 대해서도 state를 어떻게 정하느냐에 따라 Markov property를 만족할 수도, 만족하지 못할 수도 있다. 따라서, 내가 정의한 state가 Markov property를 만족하는지를 꼭 체크해보자.

Markov Reward Process

Markov reward process (MRP)는 MP에 reward라는 개념을 추가한 것으로, $\langle S,P,R,\gamma \rangle$로 나타낸다.

• State의 집합: $S$

• Transition probability matrix (model): $P: S\times S \rightarrow \mathbb{R}, P_{ss’} = P(S_{t+1} = s’ \mid S_t = s)$

• Reward function: $R:S\rightarrow \mathbb{R}, R_s = E[R_{t+1}\mid S_t=s]$

• Discount factor: $\gamma \in [0,1]$

Return and Value Function

MRP를 정의함으로써, return $G_t$에 대해서 정의할 수 있다.

\[G_t = R_{t+1} + \gamma R_{t+2} + \cdots = \sum_{k=0}^{H} \gamma^k R_{t+k+1}\]

즉, return $G_t$는 time step $t$부터 얻을 수 있는 reward의 discounted sum이다.

위 식을 토대로, state value function $V(s)$를 다시 정의할 수 있다.

\[V(s) = E[G_t \mid S_t=s]\]

Discount Factor

Discount factor $\gamma$는 수학적으로, 또 의미적으로 중요한 역할을 한다.

• 1보다 작은 $\gamma$는 return이 무한한 값을 가지지 않고 수렴하도록 한다.

• $\gamma$의 값은 미래의 보상에 대한 가치, 즉 time-value를 의미한다.

Episode가 유한한 경우, $\gamma=1$로 설정하기도 한다.

Markov Decision Process

Markov decision process (MDP)는 MRP에 decision라는 개념을 추가한 것으로, $\langle S,A,P,R,\gamma \rangle$로 나타낸다.

• State의 집합: $S$

• Action의 집합: $A$

• Transition probability matrix (model): $P: S\times A \times S \rightarrow \mathbb{R}, \quad P_{ss’}^a = P(S_{t+1} = s’ \mid S_t = s, A_t = a)$

• Reward function: $R:S \times A\rightarrow \mathbb{R}, \quad R_s^a = E[R_{t+1}\mid S_t=s, A_t = a]$

• Discount factor: $\gamma \in [0,1]$

Transition probability matrix과 reward function에 action term이 추가된 것을 볼 수 있다.

Policy

MDP에서 policy $\pi$는 주어진 state에서의 action에 대한 distribution으로 정의된다.

\[\pi(a\mid s) = P(A_t = a \mid S_t = s)\]

MDP의 policy는 history가 아니라 현재 state에 의해 결정된다. 즉, policy는 stationary (time-independent)하다.

Transition Probability and Reward Function with Policy

Policy $\pi$를 이용해서 state 간의 transition probability와 reward function을 다음과 같이 쓸 수 있다.

\[P_{ss'}^\pi = \sum_{a\in A} \pi(a\mid s) P_{ss'}^a, \quad R_s^\pi = \sum_{a\in A} \pi(a\mid s) R_s^a\]

Value Function with Policy

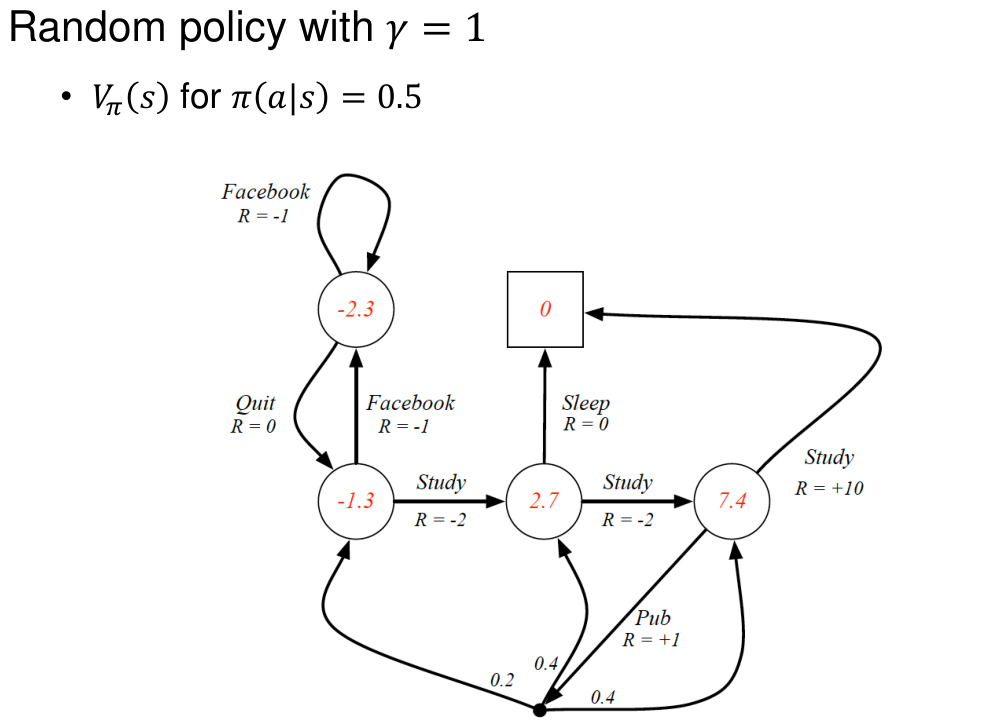
Policy $\pi$를 이용해서 value function을 다음과 같이 쓸 수 있다.

\[V_\pi(s) = E_\pi[G_t \mid S_t=s]\]

Action-value (Q-value) Function

State에 대한 value function 뿐만 아니라, state-action pair에 대해서도 value function을 정의할 수 있다.

\[Q_\pi(s, a) = E_\pi[G_t \mid S_t=s, A_t=a]\]

$Q_\pi(s, a)$는 state $s$로부터 action $a$를 선택할 때, policy $\pi$ 하에서의 return에 대한 기댓값을 의미한다.

Example of MDP