Logistic Regression
주어진 data, 또는 feature vector X,에 대해, 해당 data가 어떤 category에 포함될 지를 결정하는 것을 classification이라고 한다. 이는 X가 각 category C에 포함될 확률을 통해 결정된다.
Classification with Linear Regression
예를 들어, ‘No’이면 Y=0, ‘Yes’이면 Y=1인 간단한 classification 문제를 생각해보자. 이를 Y에 대한 X의 linear regression을 통해 prediction value가 0.5보다 크면 ‘Yes’, 작으면 ‘No’로 결정한다고 하면 어떨까?
언뜻 생각하면 효과적인 방법이나, linear regression을 통한 계산은 확률이 0보다 작거나 1보다 큰 값이 나타날 수 있고, error가 Gaussian distribution을 (결코) 따를 수 없기에 적합하지 않다. Multiclass classification을 고려한다면, linear regression을 이용한 classification은 더욱 적절치 않다.
Logistic Regression for Binary Classification
따라서, 이러한 classification에 특화된 regression model인 logistic regression이 등장하게 된다.
\[\Pr(Y=1\mid X=x)=\frac{\exp(\beta_0+\beta_1x)}{1+\exp(\beta_0+\beta_1x)} = \frac{1}{1+\exp(-(\beta_0+\beta_1x))}\]위 형태의 함수를 sigmoid 함수라고 한다.
$\Pr(Y=1\mid X=x)$는 항상 0과 1 사이의 값을 갖는다.
Linear regression과 마찬가지로 $\beta_1$이 중요하다. $\beta_1>0$인 경우에는 $X$가 커질수록 $\Pr(Y=1\mid X=x)$가 1이 될 확률이 높기에 $Y$가 ‘Yes’로 분류될 가능성이 높아지며, 반대도 성립한다.
Logistic regression 역시 기본적으로 linear model로써, feature와 response 간의 관계를 linear하게 한다.
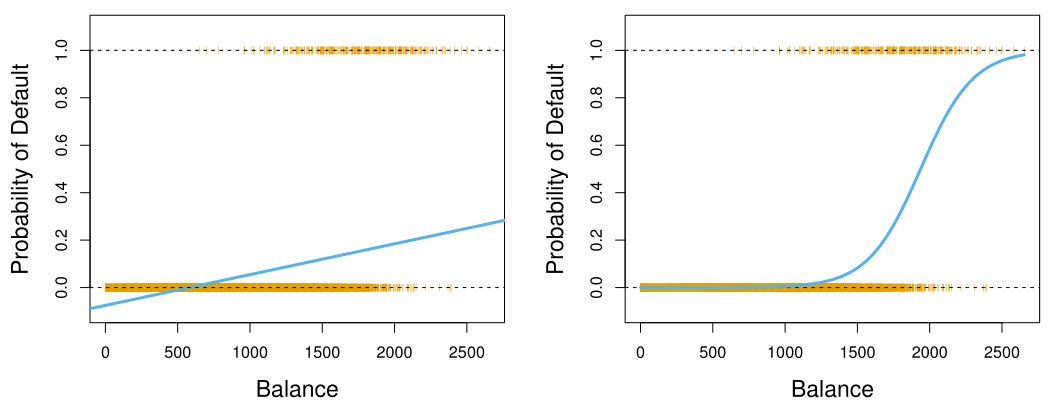
다음 그림은 linear regression과 logistic regression을 통한 classification 예시이다.
Multivariate Logistic Regression
Logistic regression 식을 multiple feature에 대해 logit form으로 표현하면 다음과 같이 쓸 수 있다.
\[\log \left( \frac{\Pr(Y=1\mid X=x)}{1 - \Pr(Y=1\mid X=x)} \right) = \beta_0 + \beta_1 x_1 + \cdots + \beta_p x_p = x^\top \beta\]Odds & Odds Ratio
Logistic regression의 해석은 odds 및 odds ratio를 통해 이루어진다.
Odds는 다음과 같이 정의된다.
\[\text{Odds}_P(x) = \frac{P(Y=1\mid x)}{P(Y=0\mid x)}\]Odds에 대한 log term을 $p(X)$의 log odds 또는 logit이라고 부른다.
Odds ratio는 다음과 같이 정의된다.
\[\text{Odds Ratio of $P$} = \frac{\text{Odds}_P(x+1)}{\text{Odds}_P(x)} = \frac{P(Y=1\mid x+1)P(Y=0\mid x)}{P(Y=0\mid x+1)P(Y=1\mid x)}\]Odds ratio는 X가 1 unit 증가할 때, Y=1일 확률과 Y=0일 확률의 ratio가 증가하는 양을 나타낸다. 이 때, Odds ratio는 $\exp(b)$와 같다는 것이 알려져있다. 즉, odds ratio는 X의 값에 의존하지 않는다.
Odds ratio는 prior probability($P(Y=1), P(Y=0)$)에 의존하지 않는다. 따라서 case-control sampling을 통해 얻은 data에 대한 해석에 유용하게 사용된다.
Maximum Likelihood
Logistic regression에서 $\beta$에 대한 estimation은 아래 likelihood function $L$을 maximize하는 maximum likelihood estimation이 사용된다.
수식을 보다 간단하게 하기 위해 다음과 같이 정의하자.
\[p(x_i) = P(Y = 1 \mid x_i) = \frac{1}{1 + \exp(-x_i^\top \beta)}\]따라서, likelihood $L(\beta)$는 다음과 같다.
\[L(\beta) = \prod_i^n p(x_i)^{y_i} (1-p(x_i))^{1-y_i}\]일반적으로는 log-likelihood $\ell(\beta)$를 더 많이 사용한다. Log-likelihood를 maximize하는 것은 likelihood를 maximize하는 것과 동일하다.
\[\ell(\beta) = \log L(\beta) = \sum_i^n \left(y_i \log(p(x_i)) + (1-y_i) \log(1-p(x_i))\right)\]간혹 $y_i$의 값이 1 or 0이 아닌, 1 or -1으로 문제가 정의되는 경우가 있다. 이 때의 log-likelihood는 다음과 같다.
\[\begin{aligned} \ell(\beta|x_i, y_i) = -\sum_{i=1}^n \log \left(1+\exp(-y_ix_i^\top \beta)\right) \end{aligned}\]
Loss Function
Loss function은 model의 prediction이 얼마나 잘못 되었는지를 측정하는 함수로, regression model에서 RSS 또는 MSE에 해당한다.
Logistic regression에서 loss function은 주로 negative log-likelihood를 사용한다. 따라서, MLE와 loss function optimization은 결과적으로 동일하다.
\[\text{Loss}(\beta) = -\ell(\beta) = -\sum_i^n \left(y_i \log(p(x_i)) + (1-y_i) \log(1-p(x_i))\right)\]이 loss function은 cross-entrophy loss 또는 log loss라고도 불린다.
Multiclass Logistic Regression
3개 이상의 class에 대한 logistic regression은 multiclass logistic regression 또는 multinomial regression이라고 하며, 이는 binary classification과 마찬가지로 $Pr(Y=k\mid X)$의 크기에 따라 classification을 진행한다.
\[\Pr(Y = k \mid X = x) = \frac{\exp(x^\top \beta_k)}{\sum_{l=1}^K \exp(x^\top \beta_l)}\]위 형태의 함수를 softmax 함수라고 한다.