LSTM and GRU
- 참고: RNN
Vanishing and Exploding Gradient Problems in RNN
RNN은 sequential data를 학습하는 것에 있어서 좋은 framework였지만, 한 가지 큰 문제를 가지고 있었다. 바로 vanishing/exploding gradient라는 문제이다. 이는 backprop 과정에서 path를 거칠수록 gradient가 사라지거나, 매우 큰 값으로 발산하는 문제를 말한다.
일반적으로 vanishing/exploding gradient 문제는 모든 종류의 neural net에서 발생할 수 있는 문제이나, RNN에서는 특히 심각하게 나타나는 경향이 있다. RNN은 일반적인 backprop이 아닌 BPTT를 진행하기 때문에, 긴 sequence를 처리할 때, 많은 time step을 거쳐 gradient가 전파된다. 즉, RNN에서는 model의 크기가 작더라도 input의 길이가 길면 vanishing/exploding gradient 문제가 발생할 수 있다. 또한, RNN은 순환 구조를 가지고 있기 때문에 각 time step에서 동일한 weight matrix가 반복적으로 사용되고, 이는 vanishing/exploding gradient 문제를 심화시킬 수 있다.
이를 수식으로 확인해보자. RNN에서의 hidden state $h_t$는 다음과 같의 정의되었다.
\[h_t = \tanh (b_h + W_{hh}h_{t-1} + W_{xh}x_t)\]$h_t$의 학습을 위해서는 최종 output이 발생한 시점 $T$의 hidden state $h_T$에 대한 gradient 계산이 필요하다. 이를 chain rule로써 표현하면 다음과 같다.
\[\frac{\partial h_T}{\partial h_t} = \frac{\partial h_T}{\partial h_{T-1}} \times \cdots \times \frac{\partial h_{t+1}}{\partial h_{t}}\]위 식에 $h_t$의 정의를 대입하면,
\[\frac{\partial h_T}{\partial h_t} = W_{hh}^{T-t} \times \prod_{i=t}^{T-1} \tanh' (b_h + W_{hh}h_{i} + W_{xh}x_{i+1})\]이 된다.
일반적인 neural net에서의 gradient 전파는 path 상의 gradient의 곱으로 나타내어지지만, RNN에서는 $W_{hh}^{T-t}$와 같은 term에 의해 (*$W_{hh}$의 값이 1에 가깝지 않다면), $T-t$가 커질수록 상대적으로 gradient가 vanishing하거나 exploding할 수 있는 것을 쉽게 알 수 있다.
이러한 문제는 RNN이 긴 sequence를 학습할 때, 초기 time step의 정보가 점점 희미해져 결국 long-term dependency을 제대로 학습하지 못하거나, gradient가 exponential하게 커져 학습을 불안정하게 만든다.
Solutions for Vanishing and Exploding Gradient Problems
이러한 vanishing/exploding gradient을 해결하기 위해 다양한 방법들이 고안되었다.
Gradient Clipping
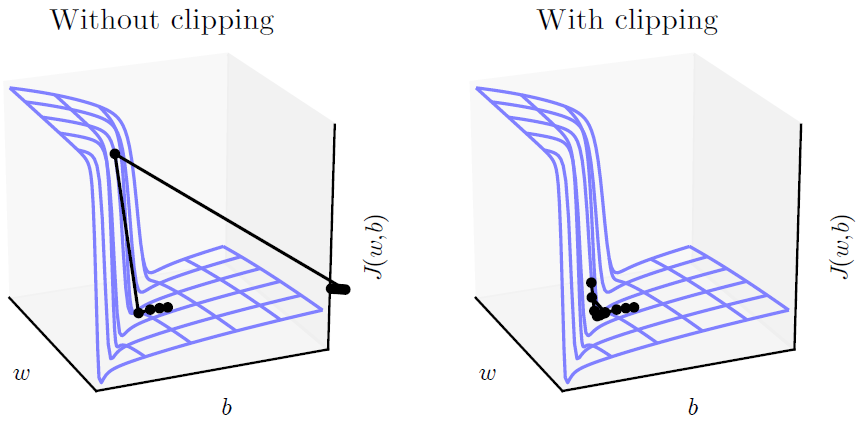
Gradient clipping은 exploding gradient 문제를 해결하기 위해 고안된 방법으로, gradient의 norm이 일정 threshold를 넘으면, parameter update를 하기 전 gradient의 norm이 threshold가 되도록 normalize하는 방법이다. 이를 통해, gradient의 방향성은 살리되 크기는 감소시켜 학습을 보다 안정적으로 진행할 수 있게 된다.
Skip Connections through Time
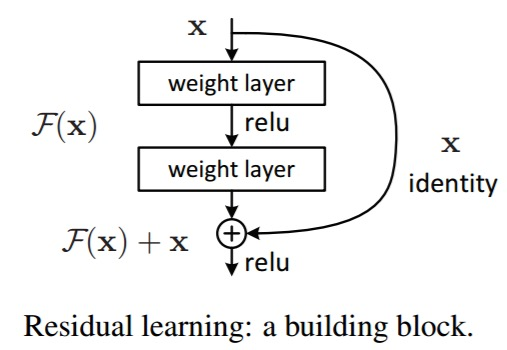
Skip connections through time이란 여러 time step들 사이에 direct connection을 추가하는 것이다 (Recap: ResNet). 이러한 direct connection은 gradient가 전파되는 path를 짧게하여 vanishing/exploding gradient 문제를 완화시킬 수 있다.
Gated RNNs
Gated RNN은 gate 구조를 추가하여 정보의 흐름을 선택적으로 조절할 수 있도록 만든 RNN 모델이다. 이는 과거 정보 중 불필요한 정보를 제거하고, 중요한 정보 만을 유지할 수 있도록 하여 vanishing/exploding gradient 문제를 해결하고 long-term dependency를 효과적으로 학습할 수 있게한다.
Gated RNN의 대표적인 모델로는 long short-term memory (LSTM)과 gated recurrent unit (GRU)이 있다.
LSTM
LSTM은 RNN에서의 hidden state를 조금 더 복잡한 구조를 갖는 cell로 대체하였다.
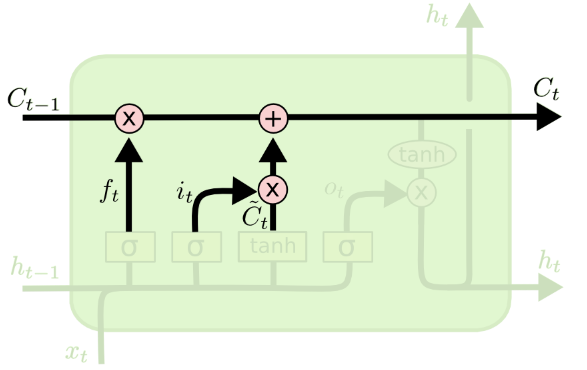
LSTM의 핵심 idea는 cell state라고 하는 $C_t$에 중요한 과거 정보를 담아서 전파를 함으로써 오래된 정보를 장기간 유지시키는 것이다. 즉, gate가 적절히 동작하게 되면 $C_t$는 훨씬 이전의 정보를 directly 갖고 있는 것과 동일한 효과를 갖게 된다. Cell state는 addition 연산을 통해 정보가 전달된다. 따라서, cell state를 통해 gradient가 직접적으로 과거의 cell에 전파되는 효과를 가지므로 vanishing gradient 현상을 완화할 수 있다.
LSTM에 존재하는 gate들은 다음과 같다.
- $f$: Forget gate, 이전 cell state $C_{t-1}$로부터 넘어온 정보 중 얼마나 많은 정보를 잊을지를 결정
- $i$: Input gate, 새로운 input data가 cell state $C_t$에 얼마나 영향을 미칠지를 결정
- $o$: Output gate, 최종 output에 대해 cell state가 얼마나 영향을 미칠지를 결정
추가로, \(\tilde{C}_{t}\)는 $x_t$와 $h_{t-1}$에 대해서 현재 cell에 대한 cell state 후보를 나타낸다 (“gate” gate 라고도 한다).
이를 기반으로 time step $t$에서의 LSTM cell의 계산을 정리하면 다음과 같다. 이 때, $U^i, U^f, U^o, U^g$와 $W^i, W^f, W^o, W^g$가 학습 대상 parameter가 된다.
$i_t = \sigma \left( x_t U^i + h_{t-1} W^i \right)$
$f_t = \sigma \left( x_t U^f + h_{t-1} W^f \right)$
$o_t = \sigma \left( x_t U^o + h_{t-1} W^o \right)$
\(\tilde{C}_t = \tanh \left( x_t U^g + h_{t-1} W^g \right)\)
- $C_t = f_t \ast C_{t-1} + i_t \ast \tilde{C}_t$
- 여기서 $\ast$는 elementwise 곱이다.
- $h_t = \tanh \left( C_t \right) \ast o_t$
즉, 현재 시점 input data $x_t$가 주어지면, 각 gate의 값 $f_t, i_t, o_t$와 cell state 후보 $\tilde{C}_{t}$를 계산하고, 이를 이용해 최종 cell state $c_t$와 output $h_t$를 계산한다.
Cell state 후보 $\tilde{C}_t$를 계산하는 과정에서는 sigmoid가 아닌 tanh를 사용하는데, 이는 최종 cell state가 덧셈을 통해 계산되므로, 항상 0 이상의 값을 갖는 sigmoid를 사용하는 경우, cell state의 값이 매우 커질 수 있기 때문이다.
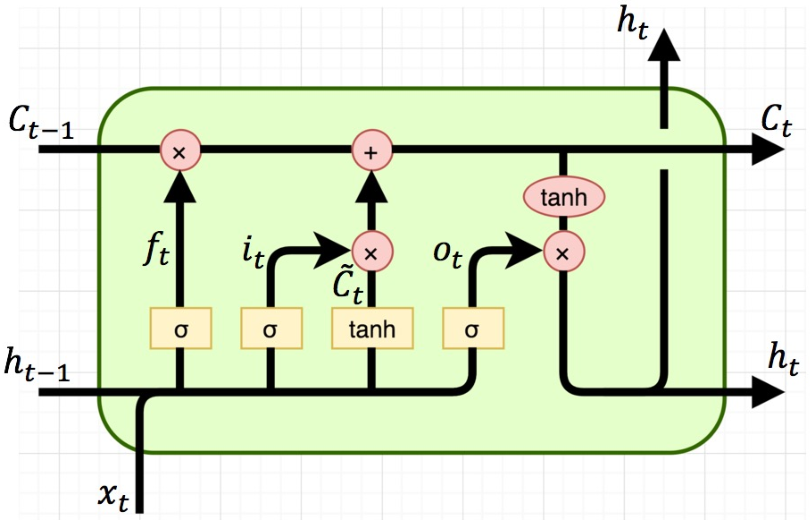
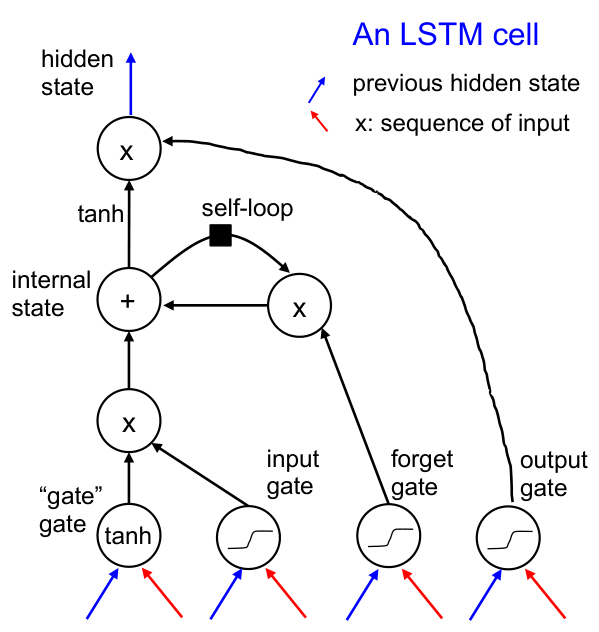
위 연산을 순차적으로 정리하면 다음 그림과 같이 표현할 수 있다. 아래 그림에서 self-loop란 현 시점에서의 forget gate $f_t$와의 연산이 직전 time step의 cell state $C_{t-1}$과 이루어지는 것을 의미한다.
LSTM은 transformer가 등장하기 전까지 약 2013~2017년 사이의 state-of-the-art (SOTA) model이었다.
Vanishing Gradient Problem in LSTM
그렇다면, LSTM에서는 vanishing gradient 문제가 완화될까?
$C_t = f_t \ast C_{t-1} + i_t \ast \tilde{C}_t$ 를 이용해서 $C_T$에 대한 $C_t$의 gradient 값을 구해보면 다음과 같이 쓸 수 있다.
\[\frac{\partial C_T}{\partial C_t} = \frac{\partial C_T}{\partial C_{T-1}} \times \cdots \times \frac{\partial C_{t+1}}{\partial C_{t}} = \prod_{i=t+1}^T f_i\]앞서 구한 RNN에서의 gradient 식과 비교해보면 상대적으로 vanishing gradient 문제가 완화된 것을 볼 수 있다.
\[\frac{\partial h_T}{\partial h_t} = W_{hh}^{T-t} \times \prod_{i=t}^{T-1} \tanh' (b_h + W_{hh}h_{i} + W_{xh}x_{i+1})\]하지만, $f_i$는 sigmoid function의 output 이기에, 0과 1 사이의 값을 갖는다. 즉, vanishing gradient 문제가 (당연하게도) 완전히 해결되지는 않는다.
GRU
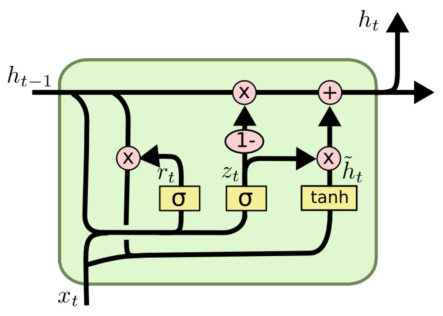
GRU는 LSTM에서 cell state라는 개념을 제거하고 hidden state를 정보 전달을 위한 매개체로 다시금 사용하며, reset gate와 update gate라는 두 개의 gate만을 사용하도록 변경한 모델이다. 이를 통해 computation 필요량과 parameter의 수를 줄일 수 있었다.
다만, LSTM과 GRU는 어느 한 쪽이 더 우수한 성능을 보여준다고 말하기는 어려우며, 실제적으로 두 모델을 모두 사용해보고 더 좋은 모델을 택하는 것이 합리적이다.
GRU에 존재하는 gate는 다음과 같다.
- $r$: Reset gate, 새로운 hidden state를 생성할 때, 이전 hidden state를 얼마나 사용할지를 결정
- $z$: Update gate, 새로운 hidden state를 얼마나 update할지를 결정
이를 기반으로 time step $t$에서의 GRU cell의 계산을 정리하면 다음과 같다.
$z_t = \sigma \left( x_t U^z + h_{t-1} W^z \right)$
$r_t = \sigma \left( x_t U^r + h_{t-1} W^r \right)$
\(\tilde{h}_t = \tanh \left( x_t U^h + \left( r_t \ast h_{t-1} \right) W^h \right)\)
$h_t = \left( 1 - z_t \right) \ast h_{t-1} + z_t \ast \tilde{h}_t$
GRU에서도 LSTM과 마찬가지로 과거 time step의 정보를 현재 time step에서 직접적으로 읽을 수 있게 하여 vanishing gradient 문제를 완화한다.