Image Restoration
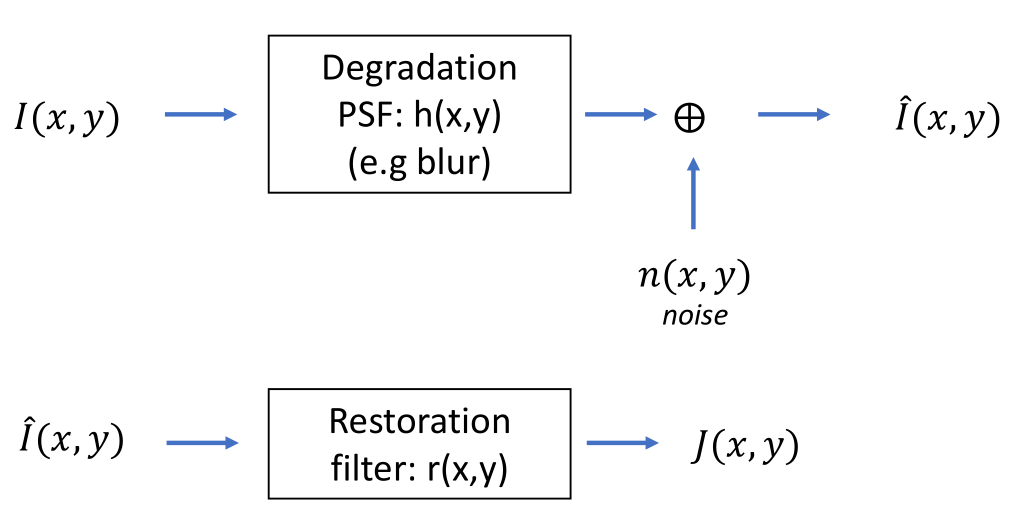
Image Restoration
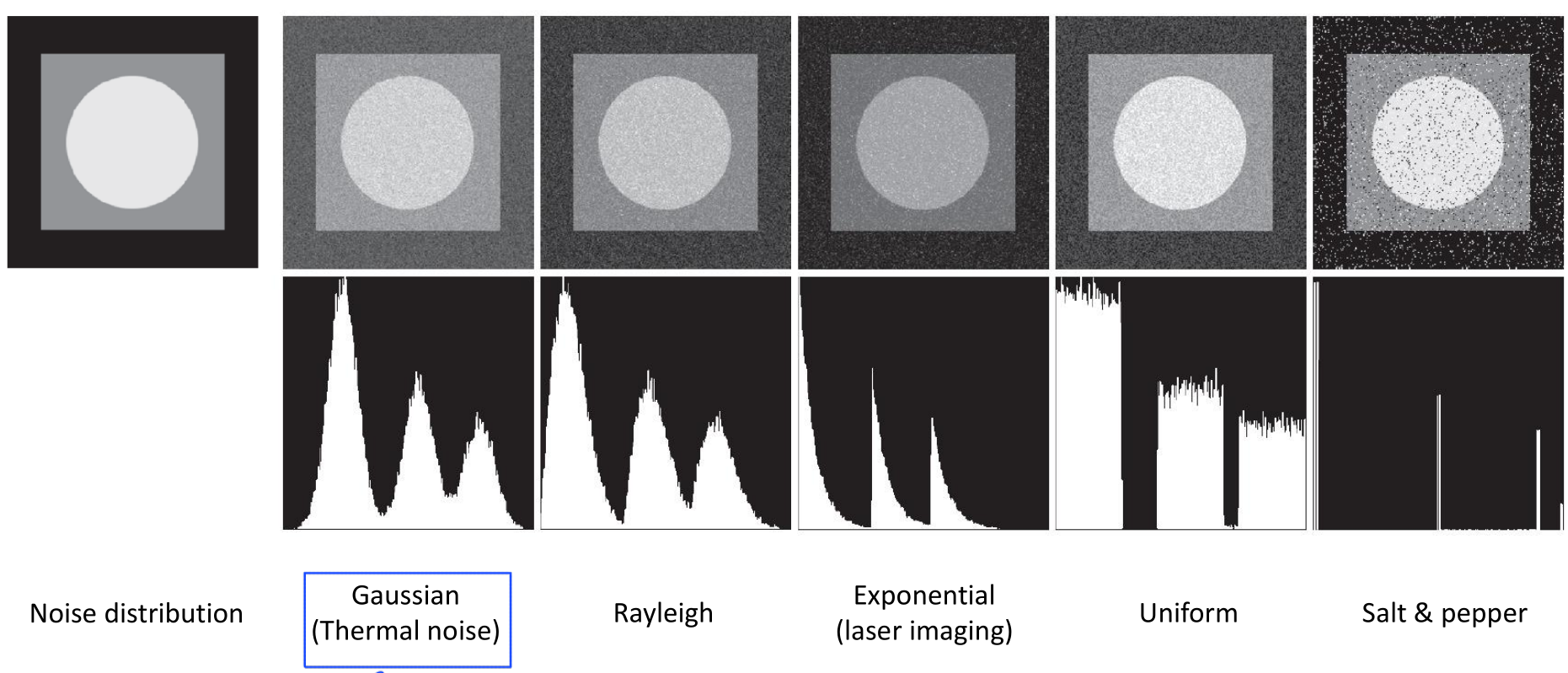
Noisy Images
Domain에 따라 다르지만, 주로 Gaussian noise를 가정
Denoising with Spatial Filter
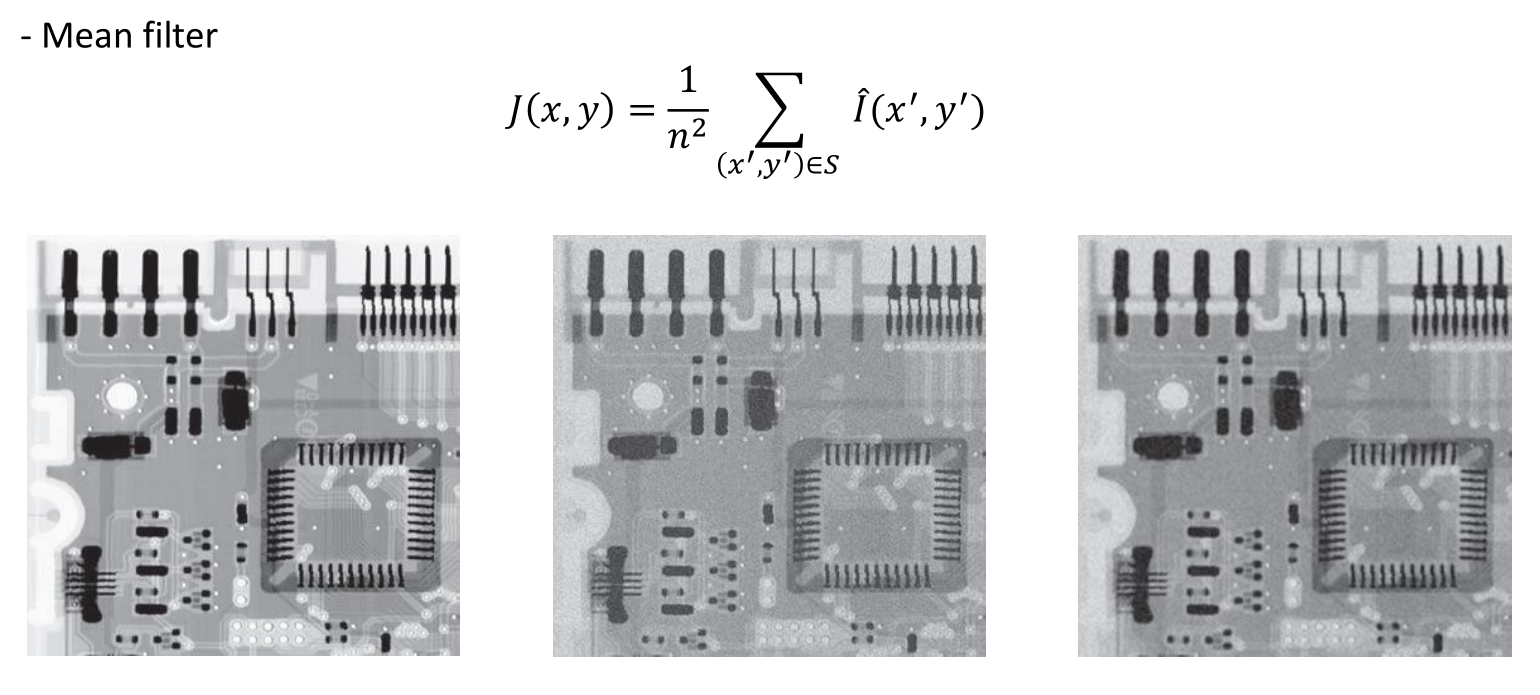
Mean Filter
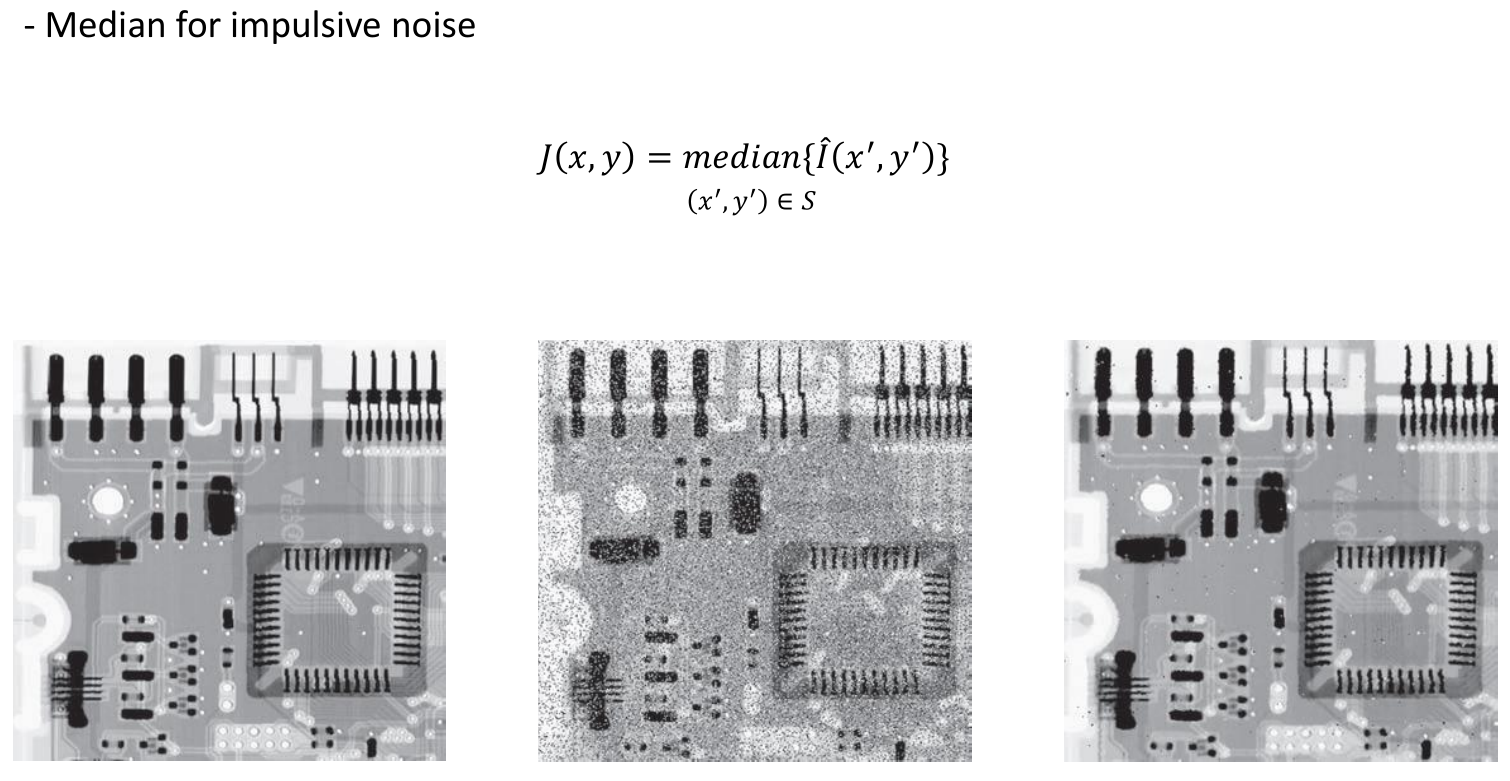
Median Filter: Impulsive Noise
Adaptive Filter
- Noise의 정도에 따라 local window를 미리 설정한다. 만약 Noise가 많으면 local window의 크기를 키운다.
- 아래 값들을 구한다.
- $\sigma_W^2$: noise variance across entire image
- $\hat{\mu}_L$: local mean around $(x,y)$
- $\hat{\sigma}_L^2$: local variance around $(x,y)$
Denoised Image $J(x,y)$를 구한다.
\[J(x,y) = \hat{I}(x,y) - \frac{\sigma_W^2}{\hat{\sigma}_L^2} (\hat{I}(x,y) - \hat{\mu}_L)\]
Adaptive filter를 적용하기 위해서는 $\sigma_W^2$에 대한 estimation이 필요하다.
- If $\sigma_W^2 = 0 \Rightarrow J(x,y) = \hat{I}(x,y)$
- If $\hat{\sigma}_L^2 \gg \sigma_W^2 \Rightarrow J(x,y) = \hat{I}(x,y)$
- Local variance가 크다는 것은 edge를 의미하기에, 그대로 유지한다.
- If $\hat{\sigma}_L^2 \approx \sigma_W^2 \Rightarrow J(x,y) = \hat{\mu}_L$
- Flat한 부분에서는 averaging
Mean, Median filter보다 성능이 더 좋은 편이다.
Notch Filter: Fourier Space Noise
Wiener Filter:
Wiener filter: minimum mean-square error filtering, i.e., $\text{minimize} \quad e^2 = E \left[ (I(x,y) - \hat{I}(x,y))^2 \right]$
Noise와 degradation이 모두 존재하는 image에 대해 효과적
Original image의 power $S_F$, Noise의 power $S_n$을 다음과 같이 정의한다.
\[S_F = |I(u,v)|^2, \quad S_n = |N(u,v)|^2\]Denoised Image $J(x,y)$를 구한다.
\[J(u,v) = \left[ \frac{H^*(u,v) S_F(u,v)}{S_F(u,v) |H(u,v)|^2 + S_n(u,v)} \right] \hat{I}(u,v)\] \[= \left[ \frac{1}{H(u,v)} \frac{|H(u,v)|^2}{|H(u,v)|^2 + \frac{S_n(u,v)}{S_F(u,v)}} \right] \hat{I}(u,v)\]
일반적으로는 $S_F(u,v)$의 값을 알지 못하기 때문에,
\[\bar{I}(u,v) = \left[ \frac{1}{H(u,v)} \frac{|H(u,v)|^2}{|H(u,v)|^2 + K} \right] \hat{I}(u,v)\]를 사용하며, $K$를 tuning parameter로 하여 값을 바꿔가면서 반복 실험을 한다.
This post is licensed under CC BY 4.0 by the author.