Frequency Domain Filters
Frequency Domain Filters
2D Fourier Transformation
주어진 2D image $f(x,y)$에 대한 Fourier Transform을 $F(u,v)$라고 하자.
2D discrete Fourier transform:
\[F(u,v) = \sum_{x=0}^{N-1} \sum_{y=0}^{M-1} f(x,y) \exp\left(-j \left( \frac{2 \pi ux}{N} + \frac{2 \pi vy}{M} \right)\right)\]2D inverse discrete Fourier transform:
\[f(x,y) = \frac{1}{MN} \sum_{u=0}^{N-1} \sum_{v=0}^{M-1} F(u,v) \, \exp\left(j \left( \frac{2 \pi ux}{N} + \frac{2 \pi vy}{M} \right)\right)\]- $F(u,v)$는 complex number이다. 즉, $F(u,v) = F_R(u,v)+jF_I(u,v)$.
- $\vert F(u,v)\vert$를 the magnitude spectrum이라고 한다.
- $\arctan (F_I(u,v) / F_R(u,v))$를 the phase angle spectrum이라고 한다.
- Conjugacy: $f^\ast (x,y) \Leftrightarrow F(-u, -v)$.
- Symmetry: $f(x,y)$ is even if $f(x,y) = f(-x, -y)$
Image를 Fourier 변환하게 되면, magnitude와 phase에 해당하는 data가 image와 같은 size로 생성된다.
즉, data size가 2배가 된다.
Magnitude 공간에서 peak가 원점에서 멀어질수록 high frequency이며, peak의 방향과 원본 이미지에서의 주기 성분의 방향은 같다. (linear phase)
- Phase는 cos 함수의 시작점을 결정한다. ($\cos(2\pi ft+\phi))$
Graphical Intuition
Magnitude의 바깥 영역을 잘라내면 본래 image의 resolution이 낮아진다.
반대로 안쪽 영역을 잘라내면, 본래 image에서는 high frequency인 edge 부분만이 남게된다.
Image를 회전시키면, Magnitude 역시 같은 각도로 회전한다.
또한, 일반적으로 Magnitude보단 Phase에 정보가 더 많다.
Properties
- Shift
- Scale
- Flip
- Rotate
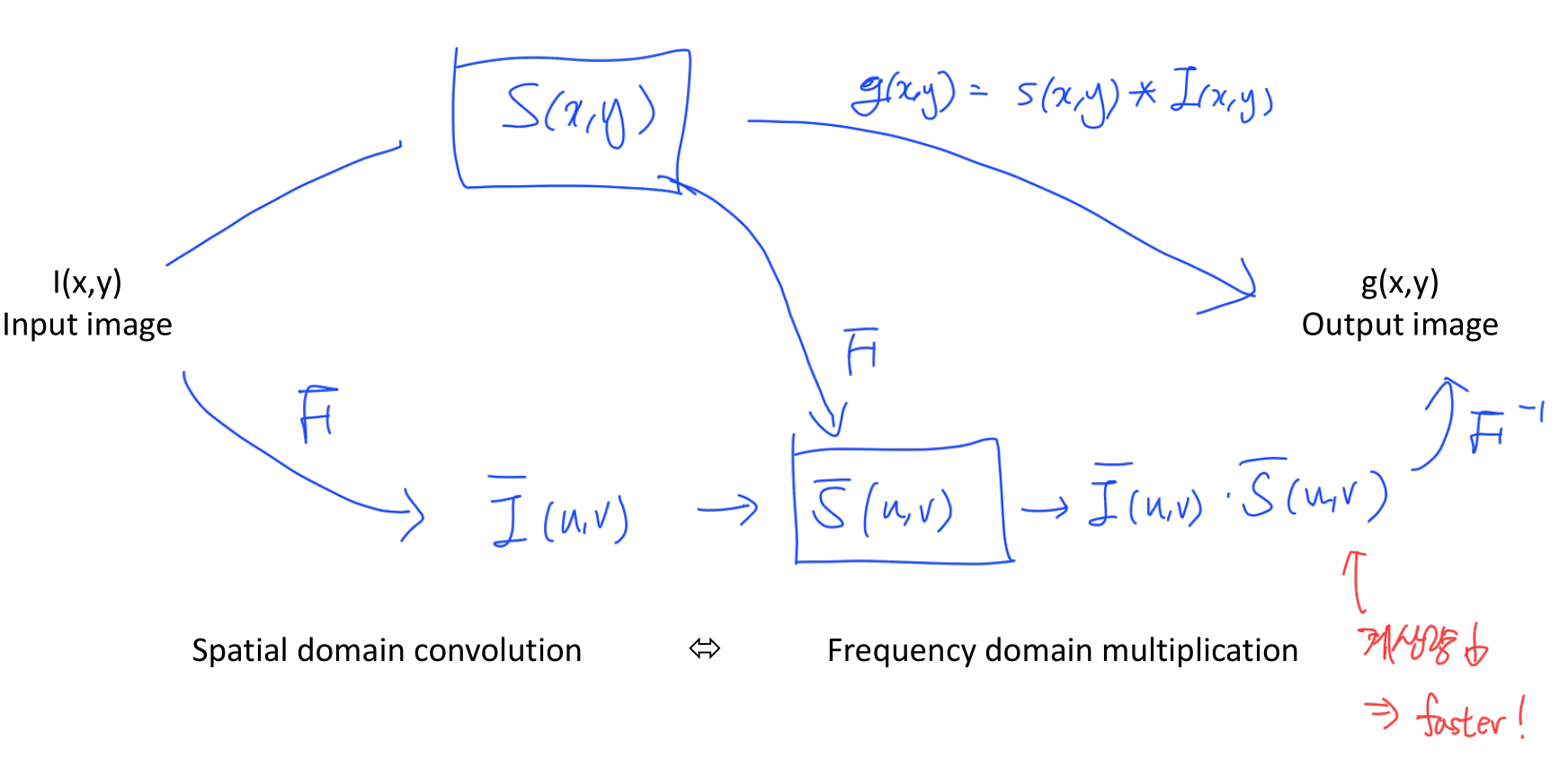
- Convolution ($\otimes$)
Frequency Domain Filters
FT를 활용한 frequency domain image processing은 kernel 방식의 image domain processing보다 빠르다.
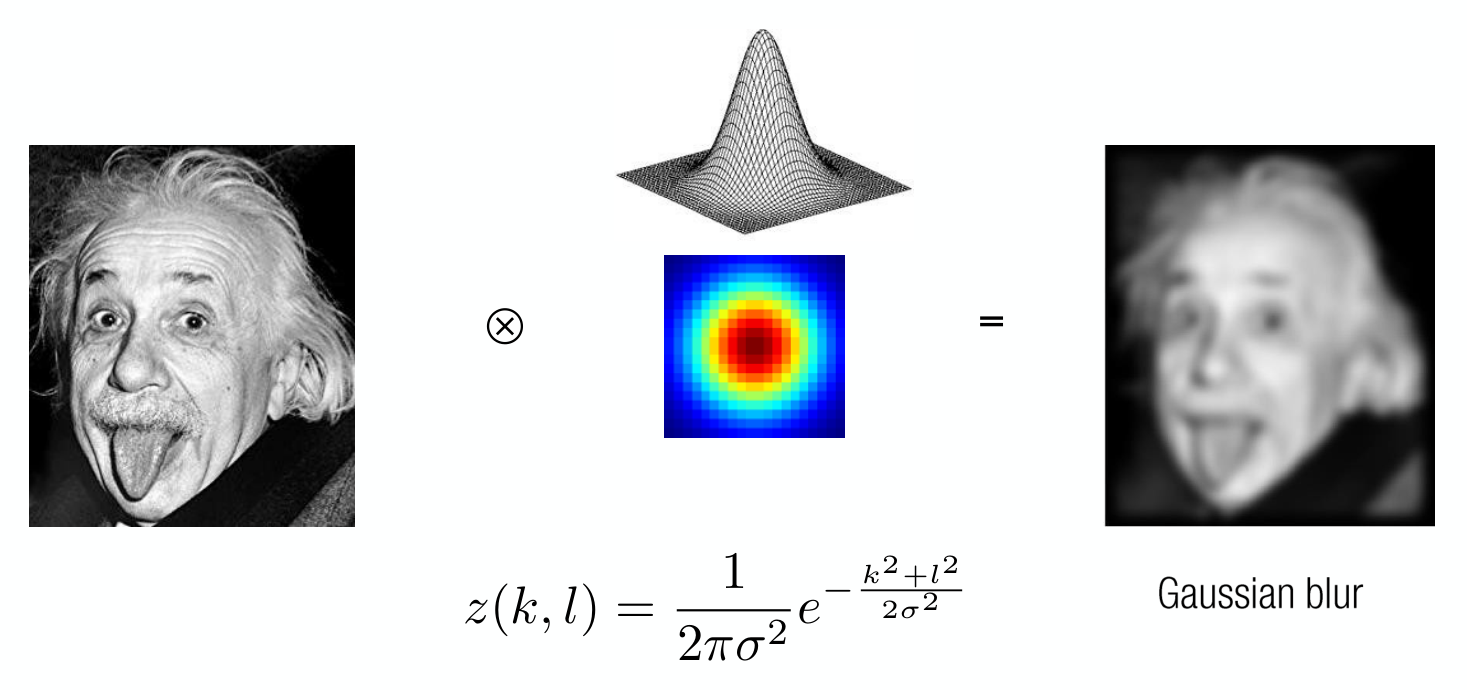
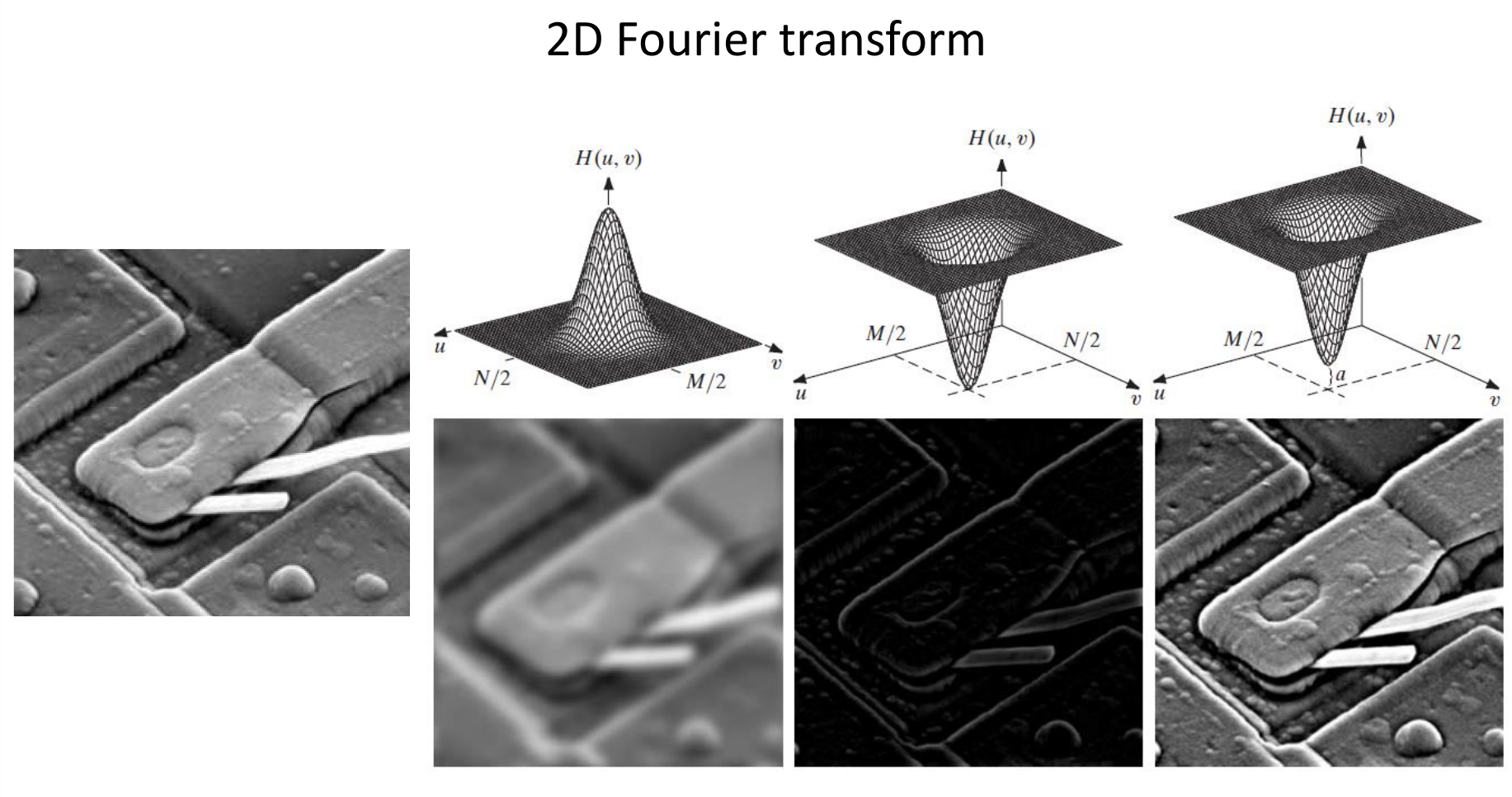
Gaussian Lowpass Filter
Gaussian은 FT 시에도, 함수가 바뀌지 않는 성질이 있어 다루기 편하다.
Laplacian Filter (Highpass Filter)
Edge detecting 및 image sharpening에 사용된다.
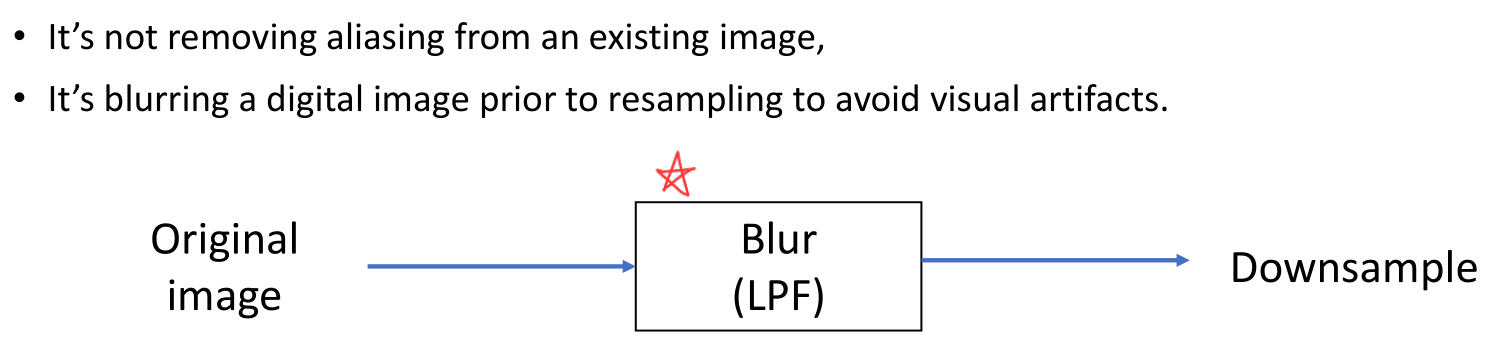
Anti-aliasing Filter
Lowpass filter를 통해 aliasing과 같은 visual artifact를 제거한다.
This post is licensed under CC BY 4.0 by the author.