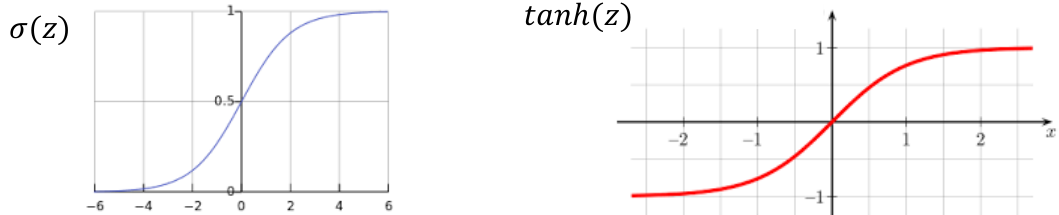FeedForward Neural Networks

FeedForward Neural Networks (FNN)

Feedforward neural network (FNN)는 가장 핵심적이고 기본적인 deep learning model이다. Deep feedforward network 또는 multi-layer perceptrons (MLP)로도 불린다.

FFN도 일종의 input $x$를 넣으면 output $y$가 나오는 함수 $f$에 대한 예측 model $f^\ast$ 이고, data로부터 model의 parameter를 학습한다.

• Feedforward: information이 model을 통해 output으로 전달됨 ($x \rightarrow f \rightarrow y$).
• Network: $f$가 다른 함수 $f^i$의 합성 함수 꼴 ($f(x)=f^2(f^1(x))$).

Learning XOR

FNN, 즉 여러개의 layer를 갖는 model의 필요성을 말해주는 예시로는 XOR 함수 문제가 있다.

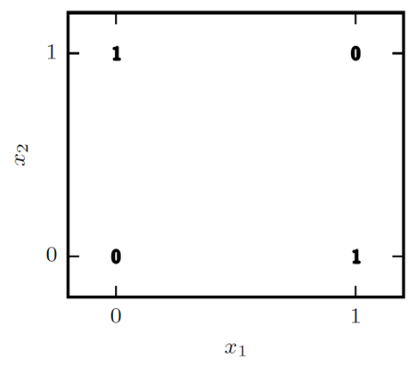
아래 그림은 binary variable $x_1$, $x_2$에 대해서 XOR 함수 적용 결과를 나타낸다. 한 눈에 보더라도 linear model로 XOR 함수를 만들어 내는 것은 쉽지 않아 보인다.

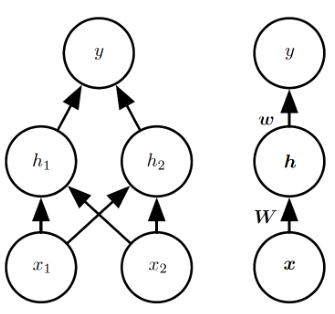
이를 해결하기 위해 하나의 hidden layer를 갖는 FNN 모델을 생각하자. 해당 hidden layer는 두 개의 hidden unit을 갖는다.

• Input unit $x=(x_1,x_2)$
• Hidden unit vector $h=f^1(x;W,c)$
• Output unit $y=f^2(h;w,b)$
• FNN 모델: $f(x;W,c,w,b)=f^2(f^1(x))$

Activation Function

만약 $f^1$, $f^2$이 모두 linear function이라고 가정하자. 이 경우, $f$ 역시 linear한 모델이 된다. 즉, XOR 문제를 풀 수 없게 된다.

따라서, 모델에 non-linearity를 부여하기 위한 작업이 필요하며, 이는 일반적으로 어떤 layer를 통해 계산된 값에 activation function이라고 하는 affine transformation을 적용하는 식으로 동작한다.

여기서는 hidden layer에 activation function $g$를 적용한다. 즉, $h=g(W^Tx+c)$이 된다.

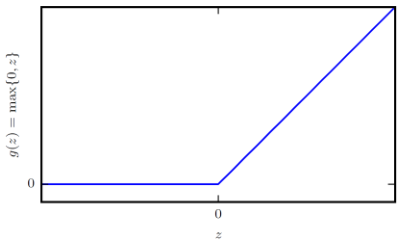
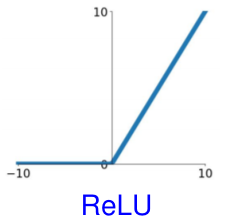
가장 널리 사용되는 activation function은 rectified linear unit (ReLU): \(g(z)=\max\{0,z\}\)이다.

Solving XOR

각 layer 통과 시에는 linear combination으로 계산된다고 가정하고, 여기에 ReLU activation function을 적용하면, FNN 모델을 다음과 같이 쓸 수 있다.

\[f(x;W,c,w,b)= w^T \max\{0, W^Tx+c\} + b\]

이 경우 \(W = \begin{bmatrix} 1 & 1 \\ 1 & 1 \end{bmatrix}, \; c = \begin{bmatrix} 0 \\ -1 \end{bmatrix}^T, \; w = \begin{bmatrix} 1 \\ -2 \end{bmatrix}^T, \; b = 0\) 가 XOR 문제의 solution이 된다.

Universal Approximzation Theorem

Hornik, Stinchcombe, and White (1989) 그리고 Cybenko (1989)의 연구에 따르면, 최소한 한 개 이상의 hidden layer를 갖는 FFN은 모든 continuous function에 대한 approximation이 가능하다.

즉, 우리가 원하는 function $f$을 FFN을 사용해서 항상 구현할 수 있다는 것이다.

다만, 그러한 $f$를 data로부터 학습하기 위한 algorithm을 상시 알 수 있는 것은 아니다.

Output Units

FFN 모델을 비롯한 deep learning 학습에는 적절한 loss function 설정이 필수적이다. 일반적으로는 cross-entropy \(J(\theta) = -\mathbb{E}_{x,y \sim \hat{p}_{\text{data}}} \log p_{\text{model}}(y\mid x)\) (참고)를 사용하며, loss function의 형태는 output unit을 어떻게 표현하는지에 따라 결정된다.

Linear Units for Gaussian Output Distributions

만약 output이 real number 형태이면, output unit은 $\hat{y} = W^th+b$로 계산된다.

이 경우, $p(y\mid x)$ 는 conditional Gaussian distribution $N(y;\hat{y}, I)$로 가정하고, loss function을 설정한다. Loss function은 mean squared error (MSE)가 된다.

\[J(\theta) = \frac{1}{N} \sum_{i=1}^N (y_i - \hat{y}_i)^2\]

Sigmoid Units for Bernoulli Output Distributions

Binary classfication 문제는 output이 0 또는 1의 값을 갖는다. 이 경우, output unit에 sigmoid function $\sigma(x)=1/(1+\exp(-x))$을 적용하여 [0, 1] 사이의 확률 값을 생성한다. 즉, $\hat{y} = \sigma (W^th+b)$이 되며, $\hat{y}$는 $y=1$일 확률이다.

따라서, loss function은 다음과 같이 쓸 수 있다.

\[J(\theta) = -y \log \hat{y} - (1-y) \log (1-\hat{y})\]

Softmax Units for Multinoulli Output Distributions

Multiclass classification 문제의 경우 output vector $y$는 $n$개의 확률 값을 갖는다. 이 경우, output unit에 softmax function $\text{softmax}(z)_i = \exp(z_i)/\sum_j\exp(z_j)$을 적용하여 $n$개의 확률값을 생성한다. 즉, $\hat{y} = \text{softmax} (W^th+b)$이 되며, 이 때의 loss function은 다음과 같다.

\[J(\theta) = -\log \text{softmax} (W^th+b)_y\]

실제 output $y$의 class가 $i$인 경우, loss는 $-\log \text{softmax} (W^th+b)_i$가 된다.

Hidden Units

Hidden unit을 어떻게 설계하는지에 대해서는 이론적으로 밝혀진 바가 많지는 않다. 일반적으론 architectural hyperparameter로 생각하고 구조를 바꿔보면서 좋은 모델을 찾는데, 최근에는 기존에 잘 동작하는 모델을 거의 그대로 가져와 사용하는 transfer learning이 일반적이다.

Non-differentiable Hidden Units

Hidden unit은 non-linearity를 주어야하면서 동시에 gradient를 적절하게 계산할 수 있어야만 gradient descent를 이용한 학습이 가능하다. 그러나, 일부 hidden unit은 모든 input에 대해서 gradient 계산이 가능한 것은 아니다 (예. ReLU는 0에서 미분 불가능).

그럼에도 불구하고, 다음과 같은 이유로 실제 gradient descent 학습은 문제없이 동작한다.

1. 거의 모든 지점에서 미분 가능하므로 미분 불가능한 지점을 만날 확률은 0에 수렴한다.

2. 미분 불가능한 지점에 대체 미분 값을 설정하여 gradient descent 알고리즘이 특정 지점에서 막히는 것을 방지한다.

3. 최적 지점(gradient가 0)에서 미분이 불가능 하더라도, 일반적인 학습은 gradient가 0에 가까운 지점에 도달하는 것이 일반적이므로 문제가 되지 않는다.

Several Hidden Units

Rectified Linear Unit (ReLU)

\[g(z) = \max \{0,z\}\]

• 쉽고, gradient vanishing problem이 없음
• 값이 0인 지점에서는 gradient-based method로의 학습이 불가
  • Dropout 효과가 있어 overfitting 방지 가능
• 주로 affine transformation ($W^Tx+b$) 위에 사용됨

Generalizations of ReLU

Negative input ($z_i<0$)에 대해 non-zero slope $\alpha_i$를 가지도록 설정한다.

\[h_i = \max (0,z_i) + \alpha_i \min (0,z_i)\]

• Absolute value rectification: $\alpha_i=-1$ ($g(z)=\vert z \vert$)

• Leaky ReLU: $\alpha_i$를 매우 작은 숫자 (0.01 등)으로 설정

• PReLU (parametric ReLU): $\alpha_i$를 learnable parameter로 설정

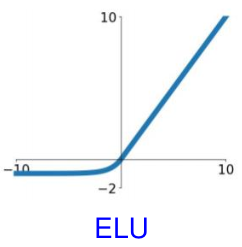
Exponential Linear Unit (ELU)

\[f(x) = \begin{cases} x & \text{if } x \geq 0 \\ \alpha (e^x - 1) & \text{if } x < 0 \end{cases}\]

$\alpha$는 일반적으로 0.1과 0.3 사이의 값으로 설정한다. Non-zero gradients를 갖지만, ReLU에 비해 계산 시간이 길어진다는 단점이 있다.

Logistic Sigmoid and Hyperbolic Tangent

ReLU 등장 이전 널리 사용되던 두 activation function으로 logistic sigmoid와 hyperbolic tangent가 있다.

• Sigmoid function: $\sigma(z) = 1/(1+\exp(-z)$
• Hyperbolic tangent: $\tanh(z) = 2\sigma(2z)-1$

두 함수는 z가 일정 크기 (대략 ±4 기준)를 넘어가면 gradient가 0으로 saturate되는 특징이 있다. 이로 인해 vanishing gradient 현상이 발생할 수 있다는 단점이 있다.