Feature Subset Selection

Feature Subset Selection

Machine learning에서 가장 중요한 것 중 하나는 올바른 feature들을 찾는 것이다. 이는 결과와 무관한 feature들을 제거하여 prediction accuracy와 model interpretability를 향상시키는 것을 말한다.

여기서는 그 방법 중 하나로 p개의 feature가 있을 때, target과 어느정도 relationship이 있는 feature의 subset을 찾는 방법인 subset selection을 소개한다.

Best Subset Selection

Best subset selection 방법은 feature의 모든 조합에 대해서 성능을 평가해보고, 가장 작은 RSS를 갖는 조합을 선택하는 방법이다.

1. Null model $M_0$으로 시작한다.
2. k=1~p에 대해,
   1. k개의 feature를 갖는 모든 model($p \choose k$개)에 대해 학습을 진행한다.
   2. 그 중 best (smallest RSS) model을 $M_k$라고 한다.
3. $M_0,\dots,M_p$ 중 optimal model을 선택한다.

하지만, computation cost 측면에서 best subset selection은 큰 p값에 대해서 사용하기 어렵다 ($2^p$번 학습 필요). 또한, overfitting 가능성 면에서도 가장 좋은 solution이라고 보기 어렵다.

이러한 이유로 상대적으로 간단한 stepwise selection 방법이 더 선호된다.

Forward Stepwise Selection

Forward stepwise selection 방법은 feature를 하나씩 추가해보면서, 가장 작은 RSS를 갖는 조합을 찾는 방법이다.

1. Null model $M_0$으로 시작한다.
2. k=0~p-1에 대해,
   1. 남아있는 p-k의 feature에 대해, 각각 model $M_k$에 추가하여 학습을 진행한다.
   2. 그 중 best (smallest RSS) model을 $M_{k+1}$라고 한다.
3. $M_0,\dots,M_p$ 중 optimal model을 선택한다.

Forward stepwise selection은 대략 $p^2/2$번의 학습만을 진행한다.

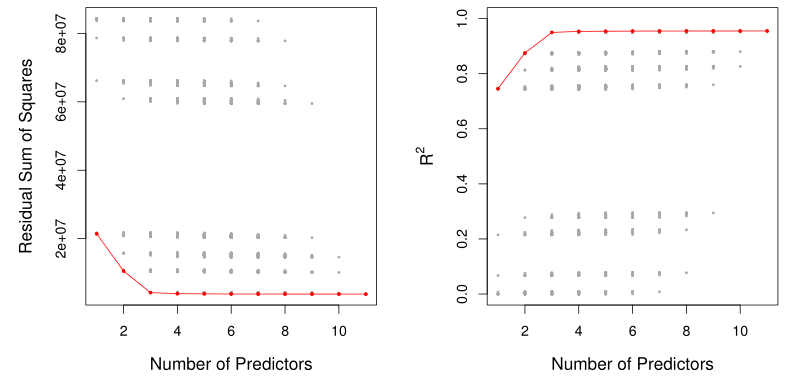
위는 동일한 feature에 대해 best subset과 forward stepwise 방법을 각각 적용했을 때의 예시이다. Best subset은 ‘# Variables’가 달라짐에 따라 best subset의 feature들이 완전히 달라질 수 있지만, forward stepwise는 직전 결과에 하나씩만 feature가 추가되는 것을 볼 수 있다.

Backward Stepwise Selection

Forward와 유사하지만 방향이 반대인 backward stepwise selection 방법도 존재한다 (학습 횟수 동일).

1. Full model $M_p$으로 시작한다.
2. k=p~1에 대해,
   1. 현재 model $M_k$에서 feature를 하나씩 빼보고 학습을 진행한다. (총 k개의 후보 model)
   2. 그 중 best (smallest RSS) model을 $M_{k-1}$라고 한다.
3. $M_0,\dots,M_p$ 중 optimal model을 선택한다.

Choosing the Optimal Model

위 subset selection 방법들에 대해서 가장 좋은 feature subset을 찾는 방법은 모든 subset 후보에 대해서 cross-validation (CV) 기법을 적용하는 것이다. 하지만 일반적으로 이는 computational cost 측면에서 어려움이 존재한다.

따라서 대개는 아래와 같은 방법으로 best feature subset을 선택한다.

1. 각 k에 대해 $M_k$를 RSS, 즉 training error를 최소화하는 model로 선정
2. 최종적으로 $M_0,\dots,M_p$에 대해 CV를 적용하여 optimal model을 선정

일반적으로 동일한 개수의 feature에서는 feature의 조합이 flexibility에 비해 RSS에 더 큰 영향을 미치고, best model들 사이에서는 RSS에 비해 flexibility에 더 큰 영향을 미치기 때문에 위와 같은 방법을 선택한다.

그러나, computation cost 측면에서 CV를 사용하기가 버거운 상황이라면, 다음과 같이 training error에 대한 보정을 통해 overfitting을 방지하는 metric를 RSS 대신 사용할 수도 있다.

여기서의 최종 feature selection 과정에서도 one-standard-error-rule을 적용한다.

Mallow’s $C_p$

\[C_p = \frac{1}{n} \left( RSS + 2d\hat{\sigma}^2 \right)\]

여기서 $d$: # of parameters, $\hat{\sigma}^2$: error의 variance의 estimate이다.

$C_p$는 model flexibility ($2d\hat{\sigma}^2$)와 training error (RSS)의 trade-off를 표현할 수 있다.

AIC

\[AIC = -2 \log L + 2 \cdot d\]

여기서 $L$: the log-likelihood of the model를 의미한다.

참고로 Gaussian error를 가진 linear model의 경우 $C_p$와 AIC는 동일하다.

BIC

\[BIC = \frac{1}{n} \left( RSS + \log(n)d\hat{\sigma}^2 \right)\]

일반적으로 7보다 큰 n에 대해서는 $\log(n)>2$이 크므로, BIC는 $C_p$보다 feature 개수에 대한 penalty가 더 크다고 볼 수 있다.

Adjusted $R^2$

\[\text{Adjusted } R^2 = 1 - \frac{\text{RSS} / (n - d - 1)}{\text{TSS} / (n - 1)}\]

Adjusted $R^2$는 기존 $R^2$에 불필요한 feature들에 대한 penalty를 주는 요소를 추가한 것으로 볼 수 있다.