Edge Detection

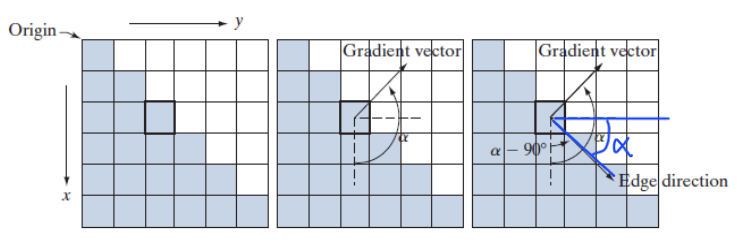
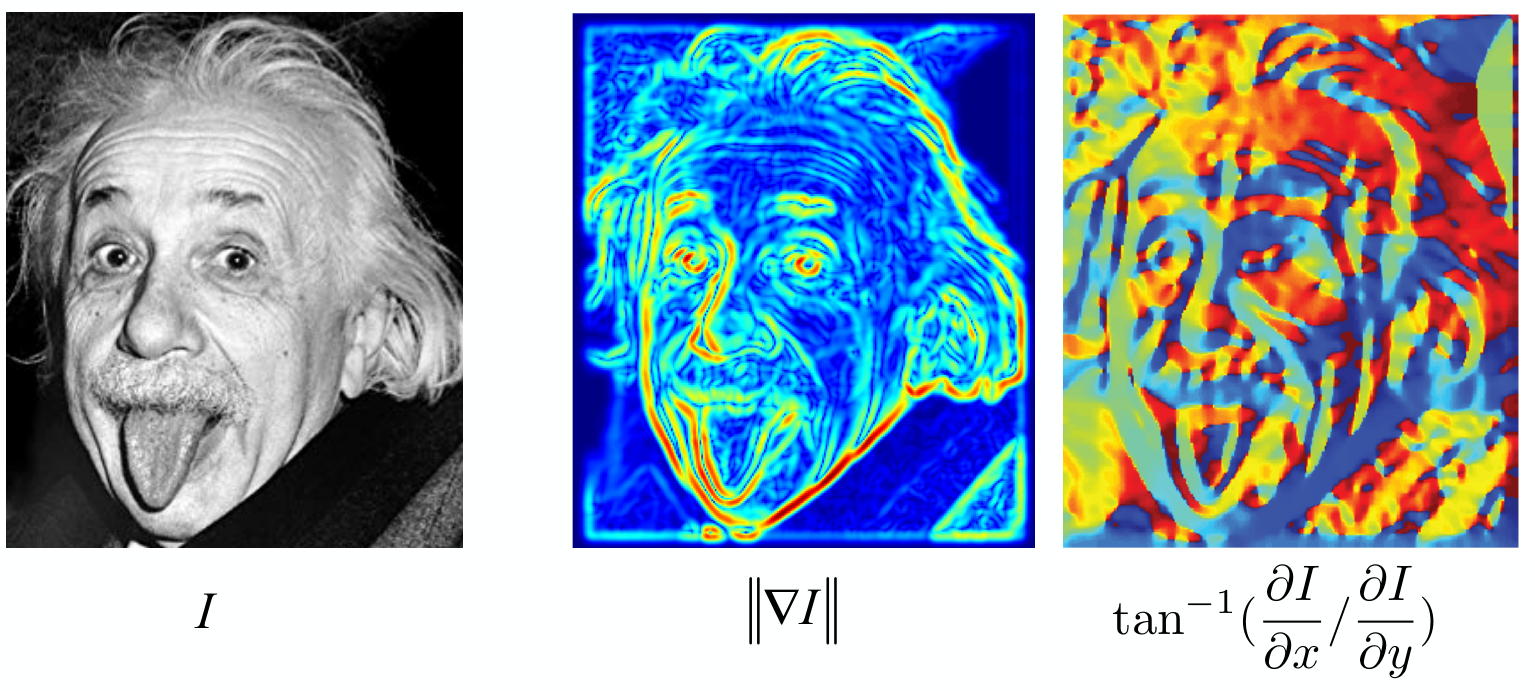
Gradients of Images

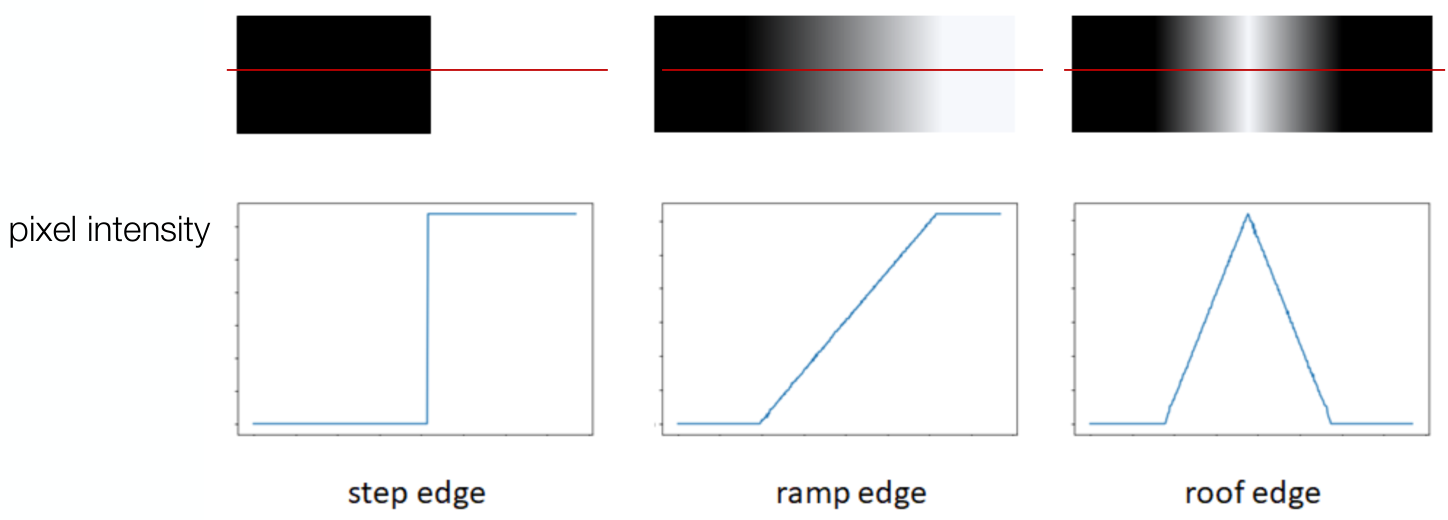
Intensity Variation at Edges

Gradients of Images

Image의 gradient $\nabla F$는 다음과 같이 정의된다.

\[\nabla F = \text{grad } F = \begin{bmatrix} \frac{\partial F}{\partial x} \\ \frac{\partial F}{\partial y} \end{bmatrix} = \begin{bmatrix} g_x \\ g_y \end{bmatrix} \approx \begin{bmatrix} F(x+1, y) - F(x, y) \\ F(x, y+1) - F(x, y) \end{bmatrix}\]

이 때, gradient를 $F(x,y)$ magnitude $M(x,y)$와 angle $\alpha (x,y)$로 분해할 수 있다.

\[M(x, y) = \sqrt{\left( \frac{\partial F}{\partial x} \right)^2 + \left( \frac{\partial F}{\partial y} \right)^2} = \sqrt{g_x^2 + g_y^2}\] \[\alpha(x, y) = \tan^{-1} \left( \frac{\frac{\partial F}{\partial x}}{\frac{\partial F}{\partial y}} \right) = \tan^{-1} \left( \frac{g_x}{g_y} \right)\]

Edge Detecting Methods

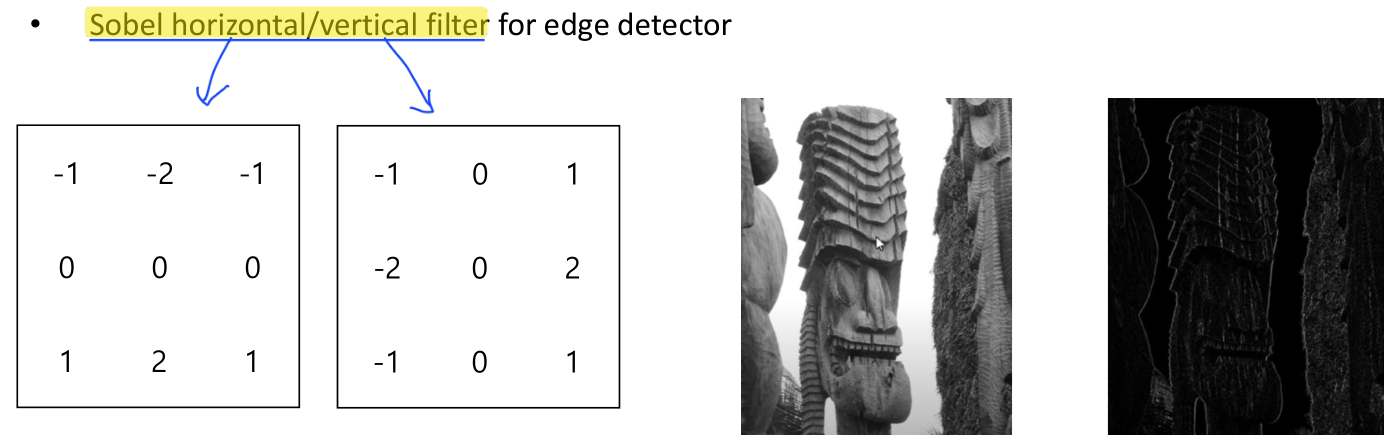
Sobel Filters

Sobel filter는 image의 1st derivative를 계산하는 필터이다. 가로/세로 방향의 filter가 각각 존재한다.

Laplacian of Gaussian

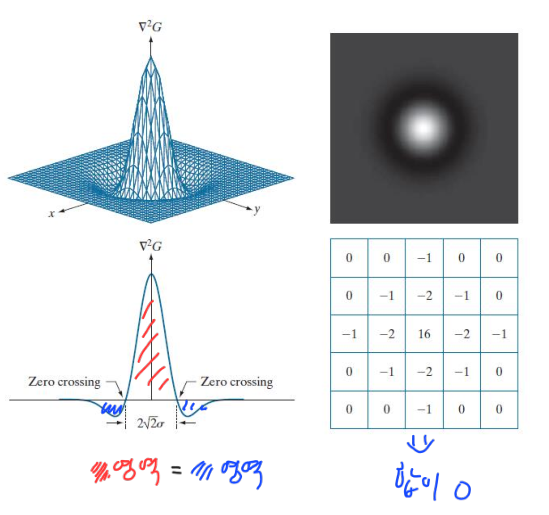
Laplacian of Gaussian(LoG)는 image에 Gaussian smoothing을 적용한 후에, Laplacian filter를 적용하는 방식이다. Laplacian filter는 Image의 2nd derivative를 계산하는 필터이다.

1. Gaussian filter $G(x,y)$를 정한다.

   \[G(x, y) = e^{\frac{x^2 + y^2}{2\sigma^2}}\]

2. LoG를 구한다.

   \[\nabla^2 G(x, y) = \frac{\partial^2}{\partial x^2} G(x, y) + \frac{\partial^2}{\partial y^2} G(x, y)\] \[= \left[ \frac{x^2 + y^2 - 2\sigma^2}{\sigma^4} \right] e^{\frac{x^2 + y^2}{2\sigma^2}}\]

Canny Edge Detector

1. Gaussian smoothing을 통해 image의 noise를 제거한다.
2. Gradient (magnitude & angle)을 계산한다.
3. Pixel이 gradient angle로부터 가장 큰 gradient magnitude를 갖는 local maximum인 경우에만 edge로 설정한다. (non-maximum suppression)
4. 두 개의 threshold($I_H$, $I_L$)를 사용해 strong edge와 weak edge를 구한다.
5. Strong edge와 weak edge 중 strong edge와 인접한 pixel들을 연결하여 edge를 완성한다. (edge linking)

주로 $I_H$는 $I_L$의 2~3배로 설정한다.