Dimension Reduction

Dimension reduction이란 high dimensional data에서 중요한 정보를 유지하면서 data의 dimension을 줄이는 기법을 말한다. 기본적으로 data를 2-dim 또는 3-dim으로 표현하게 되면 data visulalization, interpretation, processing time 측면에서 장점이 있다. 특히, curse of dimensionality의 관점에서 적절한 dimension reduction을 적용한 data는 feature selection의 효과가 있어 model의 performance를 향상시킨다.

Basic Dimension Reduction

Dimension reduction은 주로 p개의 feature를 M<p인 M-dimensional subspace로 projection하는 방법을 사용하는데, 이 때 M개의 feature들은 일반적으로 original feature들의 M개의 서로 다른 linear combinations으로 나타내어 진다.

$Z_1, Z_2, \dots, Z_M$ 을 기존 p개의 feature들의 linear combination이라고 하자.

\[Z_m = \sum^p_{j=1} \phi_{mj} X_j\]

그러면, 기존의 ordinary regression model은 다음과 같이 쓸 수 있다.

\[y_i = \theta_0 + \sum^M_{m=1} \theta_m z_{im} + \epsilon_i, \quad i=1,\dots,n\]

이 때, $\sum^M_{m=1} \theta_m z_{im} = \sum^p_{j=1} \beta_j x_{ij}$임을 쉽게 알 수 있다 ($\beta_j = \sum^M_{m=1} \theta_m \phi_{mj}$).

Dimension reduction은 $\hat{\beta_j}$에 대한 constraint를 부여하기 때문에 regularization 효과를 갖는다.

이러한 dimension reduction은 다양한 방법이 있으며, 여기서는 널리 사용되는 PCA, PLS, 그리고 MDS에 대해서 소개한다.

Principal Components Analysis (PCA)

Principal components analysis (PCA)는 data의 variance를 가장 잘 표현하는 projection axis를 찾아내어 data를 변환하는 방법을 말한다. 그러한 axis를 principal component (PC)라고 말한다.

PCA는 target의 label을 필요로 하지 않는다. 따라서, unsupervised learning의 일종이다.

The First Principal Component

PCA는 feature의 variance에 대해서만 관심이 있기에, 각 feature들에 대해서 mean이 0이 되도록 centralize했음을 가정한다.

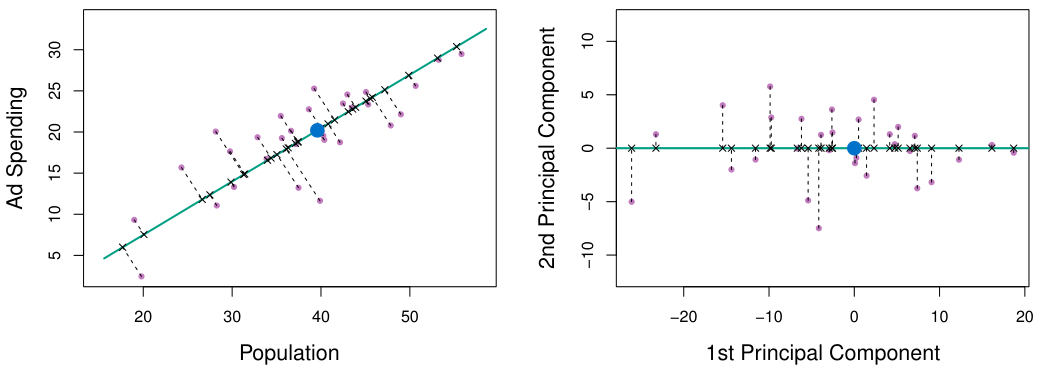
이러한 가정 하에서 첫번째 PC $Z_1$은 다음 optimization 문제의 solution $\phi$이 된다.

\[\text{maximize}_\phi \quad \frac{1}{n} \sum_{i=1}^n \left( \sum_{j=1}^p \phi_{j1} x_{ij} \right)^2 \text{ subject to } \sum_{j=1}^p \phi_{j1}^2 = 1\]

이렇게 구한 $Z_1$의 loading vector $\phi$는 data point들에 대해 가장 가까운 $p$-dimensional hyperplane을 정의한다.

PC는 normalized coefficients를 갖는 feature들의 linear combination으로 나타내어 진다. Normalization을 하지 않게 되면, $Z_1$의 variance를 증가시키기 위해 특정 $\phi_{j1}$ 값이 터무니 없이 커지는 현상이 발생 할 수 있다.

일반적으로 PCA를 진행 시에는 feature들 역시 모두 normalize하는 것이 원칙이다 (단, feature들 간의 크기 차이에 이유가 있는 경우는 제외). Parameter가 normalized된 상황이므로 feature들간 크기 차이가 발생하면 feature들의 variance를 제대로 반영할 수가 없다.

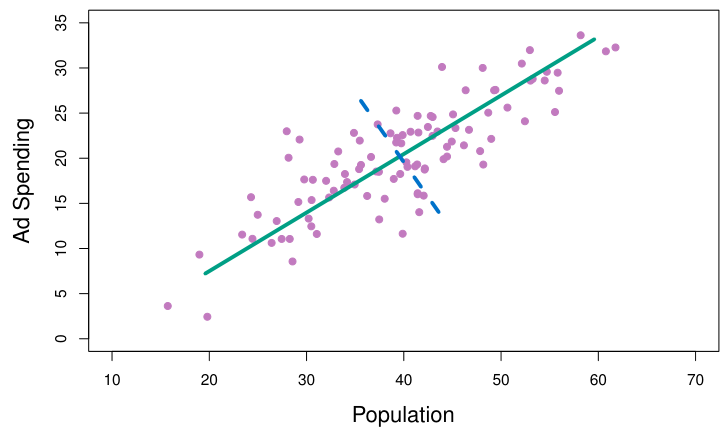
Further Principal Components

첫번째 PC $Z_1$을 찾고나면, 두번째 PC $Z_2$도 찾을 수 있다. 이는 $Z_1$과 uncorrelated된 $X_1,\dots,X_p$의 모든 linear combination 중 가장 큰 variance를 주는 vector가 된다.

즉, $Z_2$는 $Cov(Z_1, Z_2)=0$이라는 constraint 하에서 variance를 maximize하는 normalized linear combination이다.

이러한 작업을 반복하게 되면 이후 PC들 역시 구할 수 있다. 만약 우리가 가진 dataset이 $n\times p$ dimension을 가진다면, 해당 dataset은 최대 $\min(n-1,p)$개의 PC를 가질 수 있다.

실제적으로 PC를 구할 때에는 covariance matrix에 대한 singular-value decomposition을 통해 값을 계산한다.

이 때, PC들 간의 uncorrelation 제약은 geometric하게 보면 PC들이 서로 orthogonal하다는 것을 의미한다.

Proportion Variance Explained

각 PC가 얼마나 data를 잘 설명하는지에 대해서는 전체 data의 variance에 대한 각 PC의 variance의 비율, 즉 the proportion of variance explained (PVE)를 보면 알 수 있다.

Data set(with zero mean)의 total variance는 다음과 같이 쓸 수 있다.

\[\sum_{j=1}^p Var(X_j) = \sum_{j=1}^p \frac{1}{n} \sum_{i=1}^n x_{ij}^2\]

그리고 $m$-th PC의 variance는 다음과 같다.

\[Var(Z_m) = \frac{1}{n} \sum_{i=1}^n z_{im}^2\]

Data set의 total variance는 PC들의 variance의 합과 같다.

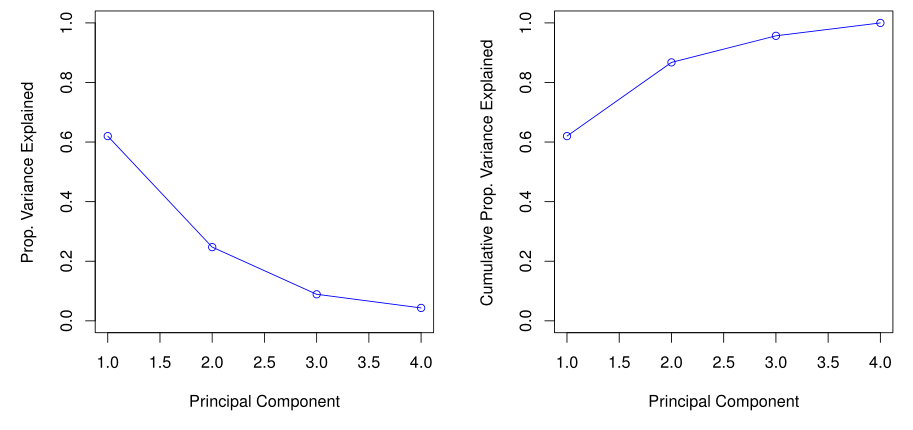
또한, $m$-th PC의 PVE는 다음과 같은 0과 1사이의 값을 가지며, 모든 PC들의 PVE의 합은 1이 된다.

\[\frac{\sum_{i=1}^n z_{im}^2}{\sum_{j=1}^p \sum_{i=1}^n x_{ij}^2}\]

일반적으로 dimension reduction을 위한 PCA의 경우 PVE의 감소가 크게 꺾이는 elbow 지점을 적절한 PC의 개수로 선택한다.

Partial Least Squares (PLS)

PCA는 기본적으로 unsupervised 방법으로, target에 대한 labeling data가 따로 사용되지 않는다.

따라서, PCA를 통한 dimension redction은 feature들을 잘 표현하는 방법으로는 볼 수 있지만 target을 예측하는 관점에서 좋은 feature인지에 대해서는 question이 존재한다.

Partial Least Sqaures (PLS)는 PCA의 이런 target과 feature들을 동시에 잘 설명하는 feature를 추출하는 방법으로, 기본적으로 target과 feature간의 covariance를 최대화하는 projection axis를 찾는다.

PLS는 다음과 같은 방법으로 $Z_1, Z_2, \dots, Z_M$를 얻는다.

1. $Z_1 = \sum_{j=1}^p \phi_{1j}X_j$으로 target Y에 대한 regression을 진행한다.
2. Regression을 통해 얻은 residual $r_{i1} = y_i-z_{i1}$을 새로운 target으로 하여, 두번째 regression $Z_2 = \sum_{j=1}^p \phi’_{1j}X_j$을 진행한다.
3. 이 과정을 M번 반복한다.

PLS는 accuracy 측면에서 특히 장점을 가지고 있다. 하지만, overfitting 가능성이 매우 높다는 단점을 가지고 있기에 사용 시에 주의해야 한다.

Multi-Dimensional Scaling (MDS)

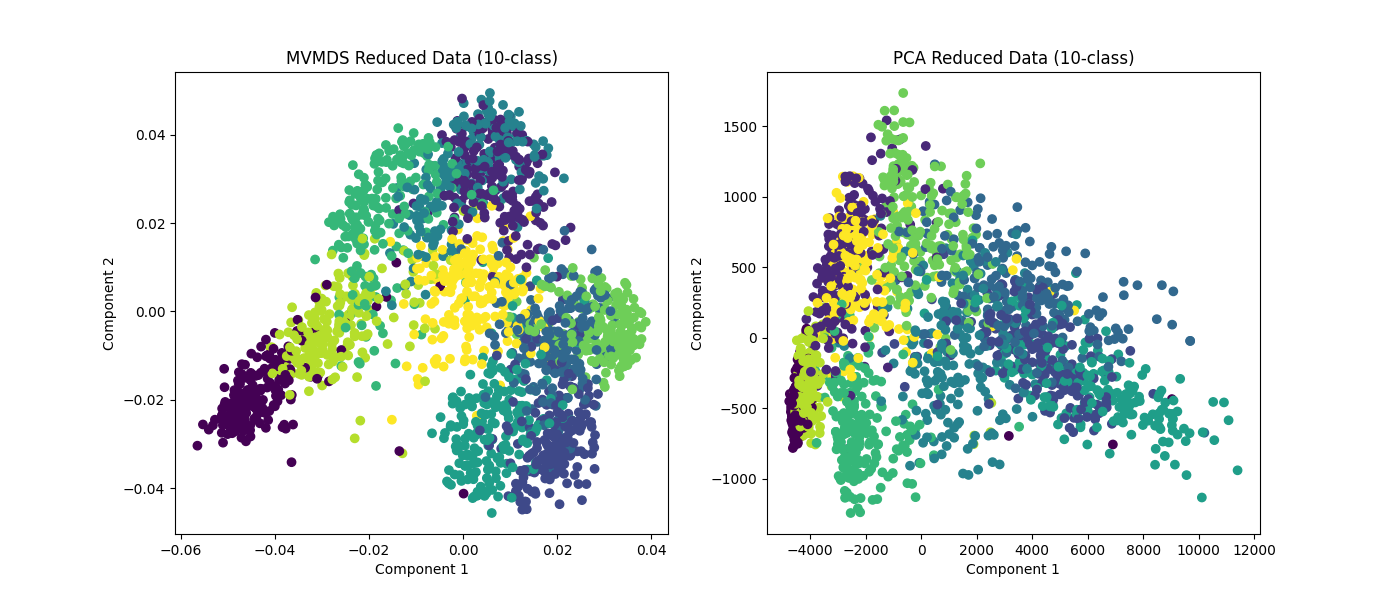
Multi-dimensional Scaling (MDS)는 data 간의 distance 또는 dissimilarity를 보존하면서 보다 낮은 dimension space로 data를 mapping한다. MDS는 PCA, PLS와는 다르게 non-linear mapping이 된다.

MDS는 dimension reduction을 통해 data point들 간의 relationship을 쉽게 파악하는 것이 주 목적이며, distance를 보존하는 mapping이라는 특성 덕분에 clustering 시에 PCA 등보다 더 좋은 성능을 보여주는 경우가 많다.

Stress Function

MDS는 stress function을 이용하여 mapping을 최적화한다. Stress function은 low-dimension space에서의 distance가 original-dimension space에서의 distance를 얼마나 잘 보존하는지를 측정하는 함수이다. Stress function의 값이 작을수록 mapping이 distance를 잘 보존한다고 볼 수 있다.

일반적으로 stress function의 값이 0.1 이하 정도 되어야 좋은 mapping이라고 판단한다.

이러한 stress function으로는 주로 STRESS 또는 S-STRESS를 사용한다.

• Kruskal’s Stress-1 (STRESS)

\[\text{STRESS} = \sqrt{\frac{\sum_{i < j} (d_{ij} - \hat{d}_{ij})^2}{\sum_{i < j} d_{ij}^2}}\]

• Standardized Stress (S-STRESS)

\[\text{S-STRESS} = \sqrt{\frac{\sum_{i < j} (d_{ij}^2 - \hat{d}_{ij}^2)^2}{\sum_{i < j} d_{ij}^4}}\]

이 때, $d_{ij}$와 $\hat{d}_{ij}$는 각각 original-dimension space에서의 distance와 low-dimension space에서의 distance를 의미한다.

S-STRESS는 distance의 제곱을 사용하기에, distance의 차이보다는 비율에 더 민감하게 반응한다.

Stress function의 값이 기준치보다 큰 값을 갖는 경우에는 mapping을 조정하거나 stress의 크기가 적정한 수준이 될 때까지 dimension을 증가시킨다. 하지만, 결과의 해석이 용이하도록 일반적으로는 2-dim 또는 3-dim을 넘기지는 않는다.