Deep Q-Learning
Value Function Approximation
SARSA와 Q-learning과 같은 model-free prediction 기법은 model의 size가 작은 경우에는 비교적 잘 동작한다. 하지만, 만약 바둑과 같이 state-action pair가 셀수없이 많은 문제에는 어떨까? 기본적으로 SARSA와 Q-learning은 직접 방문한 state-action pair에 대해서만 value update가 이루어진다. 즉, 무수하게 많은 경험을 얻지 않는 한, action-value function이 모든 state-action에 대해 제대로 update되는 것은 불가능하다.
이러한 관점에서 등장한 방법론이 value function approximation이다. 이는 value function을 어떤 parameter의 함수로 가정하고, MC 또는 TD learning을 통해 적절한 parameter를 찾아나가는 것이다.
\[\hat{v}(s, \mathbf{w}) \approx v_{\pi}(s) \quad \text{or} \quad \hat{q}(s, a, \mathbf{w}) \approx q_{\pi}(s, a)\]이러한 방법을 사용하면 우리가 일부의 경험만을 토대로 관찰하지 않은 state의 value function에 대해서도 어느정도 알아낼 수 있다.
Approximation 함수의 경우 다양한 알고리즘들이 가능하나, 가장 좋은 효과를 거둔 것은 deep learning 모델을 이용한 approximation 이다.
Deep Reinforcement Learning
Deep reinforcement learning은 deep learning 모델을 이용해 value function approximation을 하는 RL 알고리즘을 통칭한다.
일반적으로 value function, policy, model을 한꺼번에 optimize하는 end-to-end 방법론이며, 실제 value function(의 추정값)과 estimation의 차이를 이용해 parameter $w$를 업데이트하는 방식으로 학습이 진행된다.
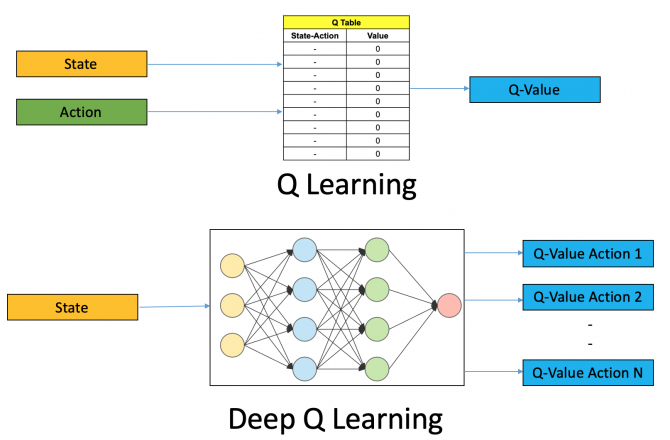
Q-value에 대한 approximation model은 input이 (state, action) pair 또는 state만을 가질 수도 있다. 이 경우, output은 각각 input에 대한 Q-value (single output) 또는 해당 state에서 가질 수 있는 action들의 q-value들 (multi output)이 된다.
Approximate the Action-value Function
Action-value function에 대해 approximation을 진행한다고 하자.
\[\hat{q}(s, a, \mathbf{w}) \approx q_{\pi}(s, a)\]이 경우, SGD 등을 이용하여 parameter $w$에 대한 update가 필요하다. 이 때의 loss function $\mathcal{L}(w)$은 다음과 같이 정할 수 있다.
\[\mathcal{L}(w) = \mathbb{E}_{\pi} [(q_{\pi}(s, a) - \hat{q}(s, a, w))^2]\]위 식을 통해 gradient를 구하면 다음과 같다.
\[-\frac{1}{2} \frac{\partial \mathcal{L}(w)}{\partial w} = (q_{\pi}(s, a) - \hat{q}(s, a, w)) \nabla_{w} \hat{q}(s, a, w)\] \[\Rightarrow \Delta w = \alpha (q_{\pi}(s, a) - \hat{q}(s, a, w)) \nabla_{w} \hat{q}(s, a, w)\]Deep Q-learning
Deep Q-learning 모델은 우리가 알지 못하는 true Q-value $q_{\pi}(s, a)$를 Q-learning의 TD target으로 간주한 모델이다. 이 때, Q-value를 추정하는 모델을 Q-network라고 한다.
\[\Delta w = \alpha (R + \gamma \max_{a'} Q(s', a', w) - \hat{q}(s, a, w)) \nabla_{w} \hat{q}(s, a, w)\]Stability Issues with Deep RL
Deep Q-learning 모델에 대해서 위 식으로 바로 학습을 진행하면 학습이 무척 불안정하게 진행된다. 이러한 현상은 크게 세 가지 이유가 있다.
- Input data가 non-iid하다.
- Agent의 experience는 time-series data의 성격을 띄므로 input간 correlation이 매우 높다.
- Q-value의 작은 변화에도 policy가 크게 바뀔 수 있다.
- Q-network의 parameter가 update되면, 전체 Q-value가 바뀌는 효과가 나타난다. 이로 인해, policy가 수렴하지 못하거나, 또는 sample의 분포가 극단적으로 바뀔 수도 있다.
- Reward 및 Q-value의 크기가 예상보다 클 수 있다.
- 예상보다 큰 Q-value 또는 reward가 들어오게 되면, exploding gradient 현상이 발생하여 학습이 불안정해질 수 있다.
Experience Replay
우선 input data가 non-iid하여 생기는 학습의 불안정 및 local optimum 수렴을 방지하기 위해 replay memory $\mathcal{D}$에 agent의 experience를 저장해두고, 해당 replay memory에서 batchsize 만큼의 sample을 random하게 골라내어 학습에 사용한다. 이러한 방식을 experience replay라고 한다.
Experience replay는 off-policy 알고리즘에서만 사용할 수 있다.
- Agent가 transition을 진행할 때마다, experience $(s_t, a_t, r_{t+1}, s_{t+1})$를 replay memory $\mathcal{D}$에 저장
- 만약 $\mathcal{D}$의 크기가 가득찬 경우, 가장 오래된 experience를 삭제
$\mathcal{D}$로부터 random sampling을 통해 mini-batch 구성
아래와 같이 학습 진행
\[\mathcal{L}(w) = \mathbb{E}_{s,a,r,s' \sim \mathcal{D}} \left[ \left( R + \gamma \max_{a'} Q(s', a', w) - \hat{q}(s, a, w) \right)^2 \right]\]
Fixed Target Q-network
학습 과정 중에 policy가 지속적으로 바뀌고, 또 수렴을 제대로 하지 못하는 현상을 방지하기 위해, TD target을 계산하는데 사용되는 target Q-network를 일정 학습 기간동안은 고정시켜놓는 방법을 사용한다.
Target Q-network의 parameter를 현재 Q-network의 값 $w$으로 고정한다. 고정된 parameter를 $w^-$라고 하자.
\[R + \gamma \max_{a'} Q(s', a', w^-)\]Fixed target Q-network를 true로 삼고 학습 진행
\[\mathcal{L}(w) = \mathbb{E}_{s,a,r,s' \sim \mathcal{D}} \left[ \left( R + \gamma \max_{a'} Q(s', a', w^-) - \hat{q}(s, a, w) \right)^2 \right]\]주기적으로 $w-$ update: $w- \leftarrow w$
Reward Clipping
Q-value가 너무 커지지 않도록 reward를 $[-1, 1]$과 같이 특정 범위 내로 제한하는 reward clipping 방법이 있다. 이를 통해 exploding gradient 현상을 방지할 수 있다.
하지만, 이는 reward의 크기를 제대로 구별하지 못해 학습이 제대로 진행되지 못할 가능성이 있으므로 tuning을 통해 적절한 범위를 찾는 것이 중요하다.