Decision Trees

Regresssion Decision Tree

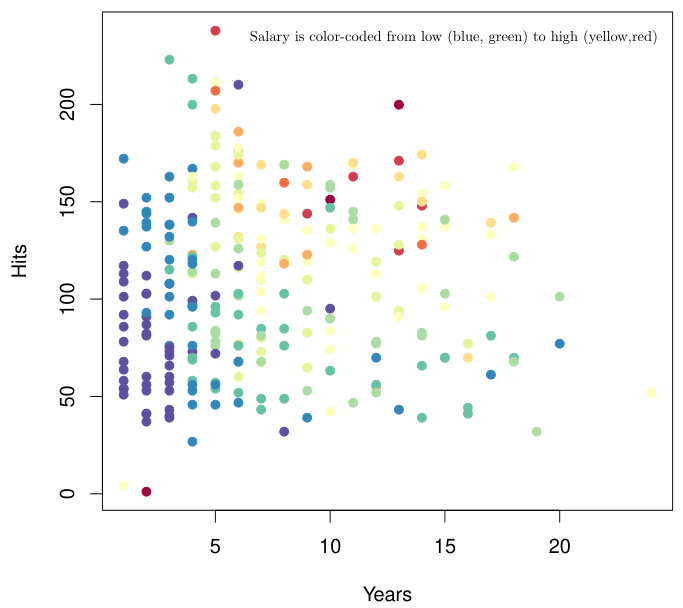
아래 예시는 야구 선수의 연차(Years)와 연간 안타 수(Hits)에 따른 연봉(Salary)를 표시한 그림이다. Salary는 낮으면 blue, 높으면 red로 표시된다.

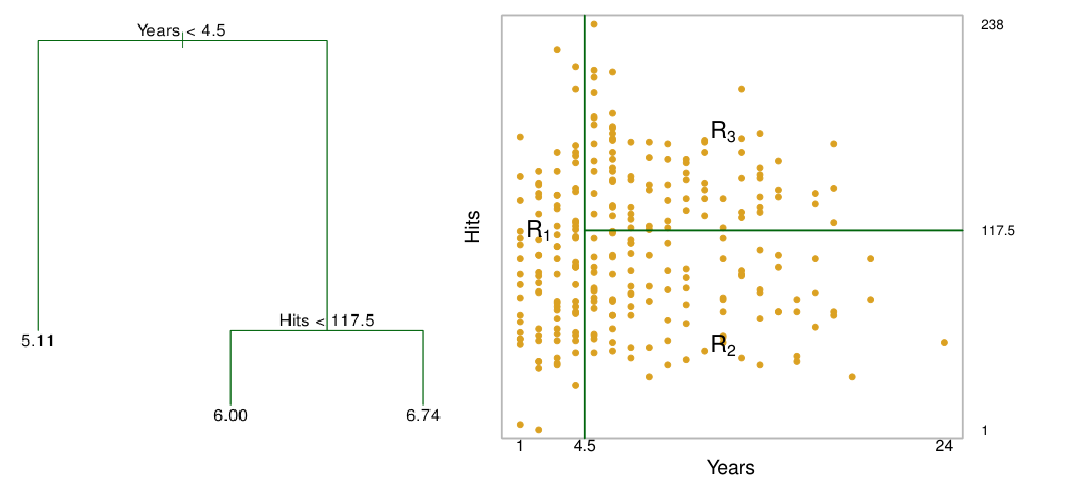
Data를 대략 살펴보았을 때, Years가 4.5를 넘는지와 Hits가 117.5를 넘는지에 따라 Salary가 달라지는 것처럼 보인다.

이 가정을 기반으로 Years와 Hits에 따른 Salary를 다음과 같은 rule로 추정할 수 있다. 해당 Rule로 나뉘어진 영역을 $R_1, R_2, R_3$로 표시하자.

이러한 형태의 rule-base regression 또는 classification을 decision tree라고 한다.

Decision tree에서 $R_1, R_2, R_3$는 terminal node라고 불리며, 최종적으로 분할된 영역이 아닌 split되는 지점 (이 예시에서는 Years<4.5, Hits<117.5)을 internal nodes라고 불린다.

매우 간단한 예시이지만, decision tree가 왜 높은 interpretability를 갖는지, 또 왜 prediction accuracy는 상대적으로 낮은지 쉽게 알 수 있다.

Tree-building Process

Decision tree의 building process은 크게 두가지로 분리할 수 있다.

1. Growing: region을 세부적으로 분리해가며 tree를 키워나가는 과정
   • 어떤 region을 나눌 것인가?
   • 어떤 feature를 기준으로 삼을 것인가?
   • 어떤 값의 cutpoint를 사용할 것인가?
2. Pruning: 부적절한 inference rule을 가지거나 불필요한 region을 제거
   • 어떤 regularization을 설정할 것인가?
   • 불필요한 region을 어떻게 판단할 것인가?

Growing

만약 $J$개의 mutually exclusive and collectively exhaustive (MECE)한 region $R_1, \dots, R_J$으로 feature space를 나눈다고 하자. 각 $R_j$에서는 모두 동일한 estimate 값 $\hat{y}_{R_j}$ (일반적으로는 train data의 mean 값)을 가지게 된다.

이 때, 목표는 결국 가장 작은 RSS를 갖도록 하는 $R_1, \dots, R_J$을 찾는 것이 된다.

\[\text{RSS} = \sum_{j=1}^J \sum_{i \in R_j} (y_i - \hat{y}_{R_j})^2\]

하지만, 이론상으로 모든 $R_1, \dots, R_J$에 대해 optimal solution을 찾는 것은 computationally infeasible하다. 따라서, 일반적으로는 recursive binary splitting이라고 알려진 top-down greedy 방법을 사용한다.

1. RSS를 최소화하는 feature $X_j$와 cutpoint $s$를 선택하여 첫번째 node를 만든다.
   • Feature space는 두 개의 region $\{X \vert X_j < s\}$와 $\{X \vert X_j \geq s\}$로 나뉘어진다.
2. 나뉘어진 region 중 하나에 대해, RSS를 최소화하는 새로운 feature와 cutpoint를 골라 두번째 node를 만든다.
   • Feature space는 세 개의 region으로 나뉘어진다.
3. Stopping criterion(각 region 별 data point의 최소 개수 등)에 도달할 때까지 위 과정을 반복한다.

Decision tree를 만드는 algorithm들은 다양하게 있으므로 (ID3, C4.5, CART, CHAID 등) 관심있으면 따로 찾아보는 것도 좋다.

Pruning

허나 training data에 대한 RSS를 최소화하는 것이 목적이 되면 overfitting 가능성이 높아진다.

이를 방지하기 위한 한 가지 아이디어로는 split을 진행하면서 감소하는 RSS가 미리 설정한 threshold 이하가 되는 경우 split을 멈추는 것이다. 하지만 RSS 감소폭이 split을 진행함에 따라 점점 작아진다는 보장이 없으므로, 이는 오히려 좋지 않은 성능의 tree를 만들 가능성이 있다.

따라서, 추천하는 방법은 가능한 큰 tree $T_0$을 만들고, 이를 잘라보며(pruning) 적절한 tree의 위치를 찾는 것이다.

Tree growing 과정에서 특정 기준(max depth, min # of nodes 등) 도달 시 tree 생성을 멈추는 것을 early stopping이라고 하며, 완성된 tree에서 불필요한 region을 제거하는 과정을 post-pruning이라고 한다.

만약 tree T의 terminal node수에 penalty를 주어 regularization 을 통한 optimal decision tree를 찾고자 한다면 다음과 같은 optimization 문제를 풀게된다.

\[\sum_{m=1}^{|T|} \sum_{x_i \in R_m} (y_i - \hat{y}_{R_m})^2 + \alpha |T|\]

여기서, $\vert T \vert$는 tree T의 terminal node 수이다. $\alpha$는 tree의 flexibility를 결정하는 hyperparameter 이기에, cross-validation을 통해 적절한 값을 찾는 것이 중요하다.

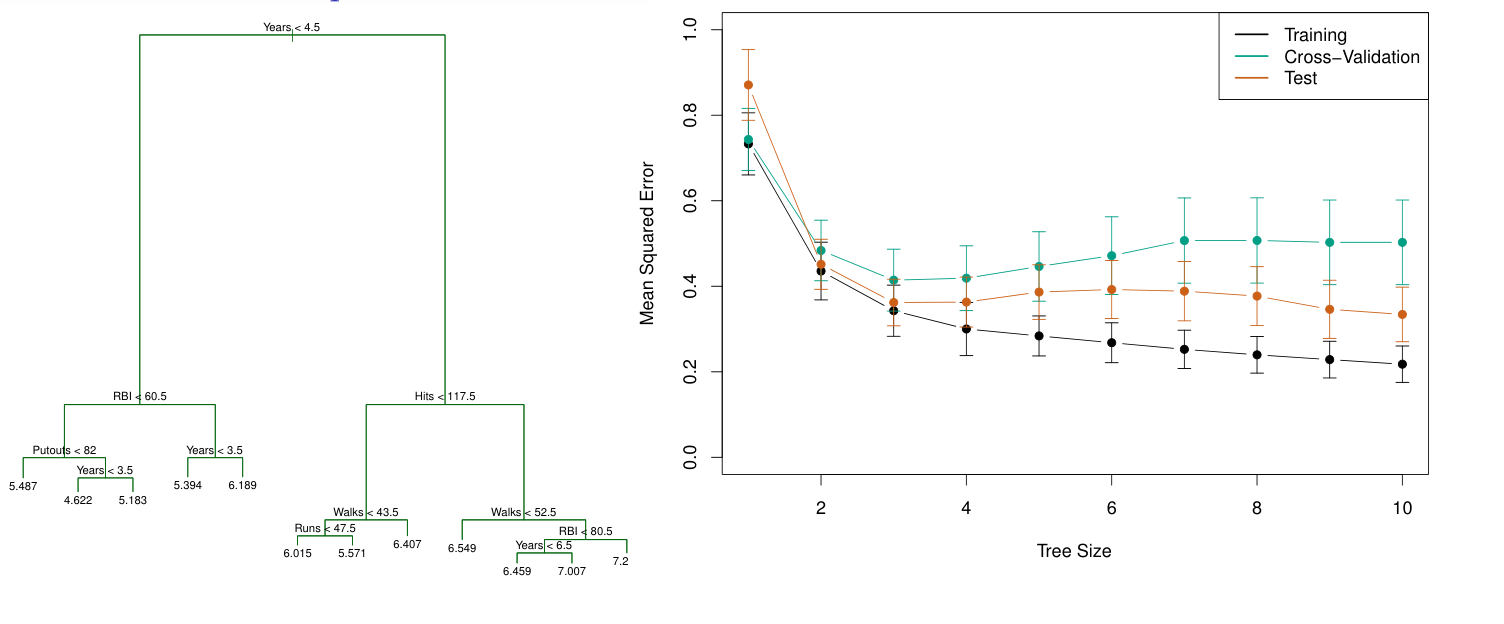
처음의 예제에 cross-validation을 적용하면 아래와 같은 결과를 얻는다. 최종적으로 CV의 최솟값에 해당하는 3(예시에서의 값!)이 최적의 tree size임을 알 수 있다.

Classification Tree

Classification tree 역시 기본적인 tree building process는 동일하며, 각 region 내 data point들의 class들 중 가장 많이 나타난 class로 예측한다 (majority voting).

Classification tree에서는 RSS가 아닌 주로 다음과 같은 impurity 지표를 사용한다.

Classfication Error Rate

Classfication error rate는 잘못 분류된 data의 비율을 측정하는 지표이다.

\[\text{E} = 1 - \max_k (\hat{p}_{mk})\]

여기서 $\hat{p}_{mk}$란 m-th region에 속해 있는 k-th class의 비율을 말한다. 즉, 하나의 region에 같은 class의 data 비율이 높을수록 error rate은 낮아진다.

하지만 classification error rate은 region 내 class의 성분 비율에 대해서는 다루지 않기에, 실제적으로는 잘 쓰이지 않는다.

Gini Index

Gini index는 한 region 내에서 data들이 얼마나 서로 다른 class를 갖고 있는지를 나타내는 지표이다.

총 $K$개의 class가 있을 때, Gini index G는 class들의 total variance를 나타낸다.

\[\text{G} = \sum_{k=1}^K \hat{p}_{mk} (1 - \hat{p}_{mk})\]

Gini index를 사용하게 되면 단순 classification error rate를 낮출 수 뿐만 아니라, node의 purity 측면 또한 향상시킬 수 있기에 유용한 지표이다.

Cross Entrophy

Cross entrophy는 information theory로부터 유래한 지표로, Gini index와 유사하게 classification error와 node의 purity을 나타낸다.

\[\text{D} = -\sum_{k=1}^K \hat{p}_{mk} \log \hat{p}_{mk}\]

현실의 classification decision tree에서는 대부분 Gini index 또는 cross entrophy를 사용한다.

Pros and Cons of Decision Trees

Decision Tree의 장점은 다음과 같다.

• 이해하기 쉬운 rule을 생성한다.
• Numeric, nominal feature 모두 취급할 수 있다.
• Feature importance를 쉽게 알 수 있다.
• Outlier에 덜 민감하다.
• Non-parametric model이다.

Decision tree는 node별 기준이 explicit하게 보여지므로 높은 interpretability를 갖는다는 장점이 있다. 또한, outlier에 덜 민감하다는 점은 decision tree가 다른 model에 비해 갖는 월등한 장점이다.

반면에, 단점으로는 다음과 같은 것들이 존재한다.

• Prediction accuracy가 (특히 regression에서 많이) 떨어진다 .
• Tree의 depth가 어느정도 깊어지면 interpretability가 떨어진다.
• Non-linearity data에 대해서 잘 예측하지 못한다.
• Data의 작은 변화에도 결과가 크게 달라질 수 있다.
• Variance가 큰 model이므로 overfitting 가능성이 크다.