Cross-validation
기본적으로 model의 성능은 test error를 기반으로 평가된다. 그러나 test set은 기본적으로 training 과정에서 알 수 없기 때문에, training 시에는 test error를 예측하는 방법이 필요하다.
Validation-set Approach
Validation-set approach 또는 hold-out approach는 우리가 학습 시에 사용할 수 있는 data를 training set과 validation set으로 나누고, training set을 통해 학습하고 validation set으로 이를 평가하여 test error를 예측하는 기법이다.
Validation-set approach를 사용하는 경우 결국 training에 사용되는 data가 상대적으로 적어지기 때문에, test error가 overestimate 될 수 있다.
또한, data set 분할이 imbalance하거나 특정 pattern을 포함하지 못할 경우, validation error가 크게 달라질 수 있다. 즉, test error estimation의 변동폭이 상대적으로 크다.
좋은 model을 얻기 위해서는 training set, validation set, test set의 data 분포가 유사해야 한다. 특히, Classification의 경우, training set의 actual class의 비율과 validation set의 actual class의 비율이 유사해야 한다.
K-fold Cross-validation
이러한 단점을 보완하기 위한 개선된 validation approach로 K-fold cross-validation (CV) 방법이 있다.
Random하게 data를 동일한 크기의 K개로 나눈다.
특정 part k를 빼고, 나머지 K-1개의 데이터로 training을 진행한다.
제외했던 part k에 대해 prediction을 얻는다.
이 과정을 k=1~K까지 반복하고, 결과를 합친다.
K-fold CV는 각 iteration 별로 서로 다른 data set으로 평가하여 평균을 취하기에, estimation의 variance 역시 hold-out approach에 비해 작다. 그러나, K의 크기에 따라 variance의 정도가 달라질 수 있으며, K가 너무 작은 경우 여전히 높은 variance를 갖는다.
일반적으로 test error의 overestimation은 적은 training data 양에 기반하므로 K-fold CV와 validation-set approach의 test error의 overestimation 가능성에는 큰 차이가 없다.
일반적으로 K는 5 또는 10으로 설정한다.
Leave-one Out Cross-validation (LOOCV)
만약 K=n (data 수)로 설정하는 경우의 CV, 즉 n-fold CV를 leave-one out cross-validation (LOOCV)라고 한다.
LOOCV의 경우 training에 사용되는 data를 가장 많이 쓸 수 있어 validation error와 test error 간의 차이(bias)가 최소화된다. 또한, 모든 sample에 대해서 error를 측정하고 평균을 취하기에 estimation variance 역시 매우 낮다. 하지만, computational cost가 무척 크다는 단점이 있다.
간혹 LOOCV 방법의 estimation variance가 크다고 설명되어 있는 경우가 있는데, 이는 평균을 취하기 전 error data들의 variance가 크다는 뜻이다. 최종 test error estimation은 평균 값이 사용되기에, LOOCV의 estimation 값은 동일한 data set에서는 항상 일정하다.
Preprocessing and CV
학습을 진행하는 과정에서 간혹 data preprocessing 또는 feature selection을 전체 dataset에 적용하고, model training에 과정에서만 CV와 같은 validation-set approach를 수행하는 경우가 있다.
하지만, 이렇게 되면 이미 모델이 test set에 대한 정보를 어느정도 반영하게 되어 error가 underestimated 되는 문제가 생긴다.
따라서, CV를 수행할 때는 꼭 data set을 미리 나누어놓고 동일한 preprocessing을 각 set에 대해서 개별로 진행해야한다.
How to Choose the Best Model?
이런 CV 기법은 기본적으로 model의 hyperparameter 또는 model의 architecture를 결정하는 데 있어서 사용된다.
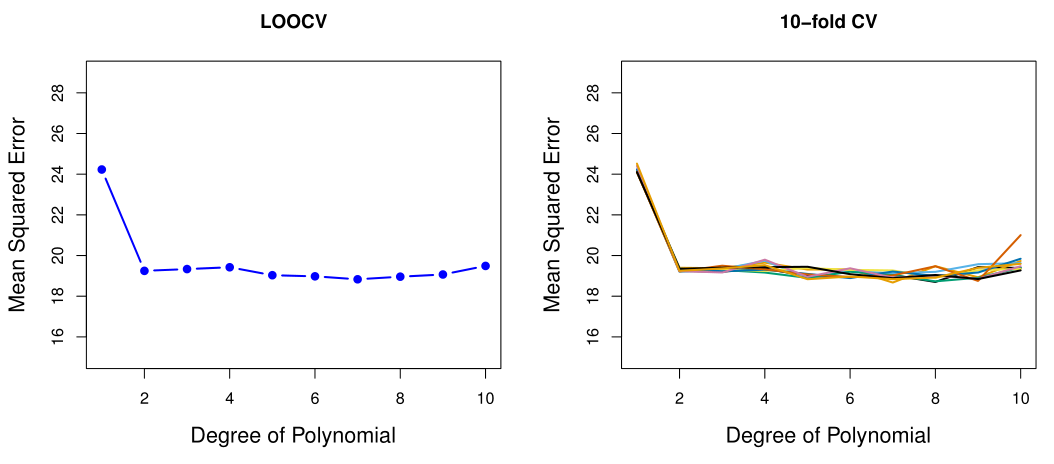
Best model을 선정하는 데 있어서 단순하게 validation error가 가장 낮은 model을 선정할 수도 있지만 (아래 LOOCV의 경우 degree=7인 model), 그러한 경우 model의 flexibility 증가에 따라 overfitting 가능성이 더 커질 수 있다.
따라서 이러한 경우, 가장 낮은 validation error를 갖는 model에 대해 MSE의 standard error $\sigma$를 구하고, 해당 error + $1\sigma$ 안쪽의 validation error 가지는 model 중 flexibility가 가장 낮은 model을 선택한다.
이를 one-standard-error rule이라고 한다 (아래 LOOCV의 경우 degree=2인 model이 선택됨).