Convex Optimization

Convexity

Convex Sets

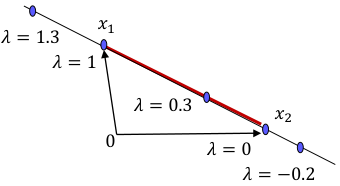
• A convex combination of two points is the line segment between them.

\[\lambda x_1 + (1-\lambda) x_2, \quad \lambda \in [0,1]\]

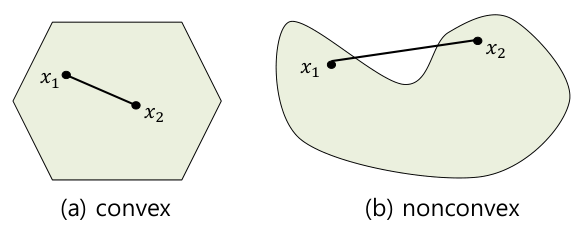
• A set $C \in \mathbb{R}^n$ is called convex if the convex combination of any two points $x_1, x_2$ in $C$ always lies in $C$.

\[\lambda x_1 + (1-\lambda) x_2 \in C, \quad \forall\lambda \in [0,1]\]

Geometrically, it is a set that does not have any inward-curving parts or holes in its interior.

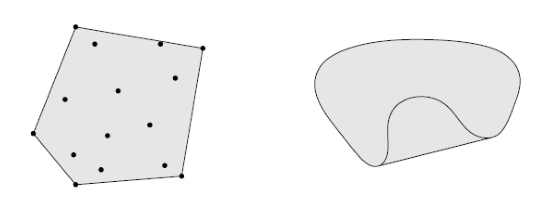
• The convex combination of all points in a set $C$ is called the convex hull of $C$, denoted as $conv(C)$.

\[conv(C) = \{\sum_{i=1}^k \lambda_i x_i | \sum_{i=1}^k \lambda_i = 1, \lambda_i \ge 0, i=1,\dots, k\}\]

$conv(C)$ is the smallest convex set that contains the set $C$.

Convex Functions

• Let $f:C \rightarrow \mathbb{R}$, where $C$ is a nonempty convex set in $\mathbb{R}^n$.
  The function $f$ is said to be convex on $C$ if $x_1, x_2 \in C$ with $0 \le \lambda \le 1$

  \[f(\lambda x_1 + (1-\lambda)x_2) \le \lambda f(x_1) + (1-\lambda)f(x_2)\]
  • concave : if $-f$ is convex on $C$.
  • strictly convex or strictly concave: if the equality doesn’t hold.

A convex function $f$ has the property that the line segment connecting any two points on its domain always lies above or on the graph of $f$.

Theorem: Jensen’s inequality

For a convex function $f$ and $\sum_{i=1}^k \lambda_i = 1, \lambda_i \ge 0$ $\forall i$,

\[f(\sum_{i=1}^k \lambda_i x_i) \le \sum_{i=1}^k \lambda_i f(x_i).\]

It can also be viewed as the expected value in probability (where the sum is 1): $f(\mathbb{E}[x])\le \mathbb{E}[f(x)]$.

Theorem: First-order conditions

Let $C$ be a nonempty open convex set in $\mathbb{R}^n$, and let $f: C \rightarrow \mathbb{R}$ be differentiable on $C$. Then $f$ is convex if and only if for any $x,y\in C$, we have,

\[f(y) \ge f(x) + \nabla f(x)^T(y-x).\]

Convex function $f$ is always greater than or equal to the tangent of a specific point $(x,f(x))$.

Convexity and Optima

Critical Points

The unconstrained optimization problem referred to here is the minimization problem.

For minimizing $f(x)$ over $\mathbb{R}^n$:

• If \(f(x^*) \le f(x)\) for all \(x\in \mathbb{R}^n\), then $x^*$ is called a global minimum.

• If \(f(x^*) \le f(x)\) for all \(x\in N_\varepsilon (x^*)\), then $x^*$ is called a local minimum.

• If $f$ is differentiable and \(\nabla f(x^*)=0\), then $x^*$ is called a critical point of $f$.

• If $x^\ast$ is a critical point, but neither a maximum nor a minimun, then $x^\ast$ is called a saddle point.

Even if it is not a critical point, a local maximum (or minimum) can still appear.

Convex Optimization Problem

• For a convex set $C$, if a function $f$ is a convex function on $C$, then $\min\limits_{x\in C} f(x)$ is called a convex optimization problem (CO).

In CO, there is a useful property that local optima are also global optima.

Theorem: Convex optimization problem

\(x^*\) is a local minimum for (CO), if and only if, \(x^*\) is a global minimum for (CO).

To verify whether a given optimization problem is CO, you must first check if the domain is a convex set, and then the Hessian matrix of $f$ on that set is positive semidefinite.

Theorem: Second-order conditions

Let $C$ be a nonempty open convex set in $\mathbb{R}^n$, and let $f:C\rightarrow \mathbb{R}$ be twice differentiable on $C$.
Then $f$ is convex if and only if its Hessian $\nabla^2f(x)$ is positive semidefinite for all $x \in C$.

Additionally, by verifying the positive definiteness of the Hessian matrix of $f$, you can show that $f$ is a strictly convex function.

Lemma:

If the Hessian matrix is positive definite, then $f$ is strictly convex.

If $f$ is strictly convex and quadratic then its Hessian matrix is positive definite at each point of $C$.

For a 2x2 matrix \(A =\left[ \begin{array}{cc} a & b \\ b & c\\ \end{array} \right]\), it is positive definite if $a>0$ and $ac-b^2>0$ hold.