Clustering

Clustering이란 대표적인 unsupervised learning 방법 중 하나로, data set에 대해서 homogeneous subgroup 또는 cluster를 찾는 기법을 말한다.

Clustering이란 기본적으로 어떤 algorithm과 measure를 사용할 지에 대해서 domain 지식과 경험을 기반으로 subjective하게 판단할 수 밖에 없기에 가장 어려운 문제 중 하나로 볼 수 있다.

Clustering algorithm을 평가하는 여러 index가 있지만, 해당 index를 절대적으로 믿어서는 안된다.

Clustering은 (돈이 되는!) advertising과 직결되는 추천 문제의 핵심 요소이기에 여전히 연구가 이루어지고 있다. 여기서는 기초적이고 대표적인 clustering algorithm 2개에 대해서만 소개한다.

K-means Clustering

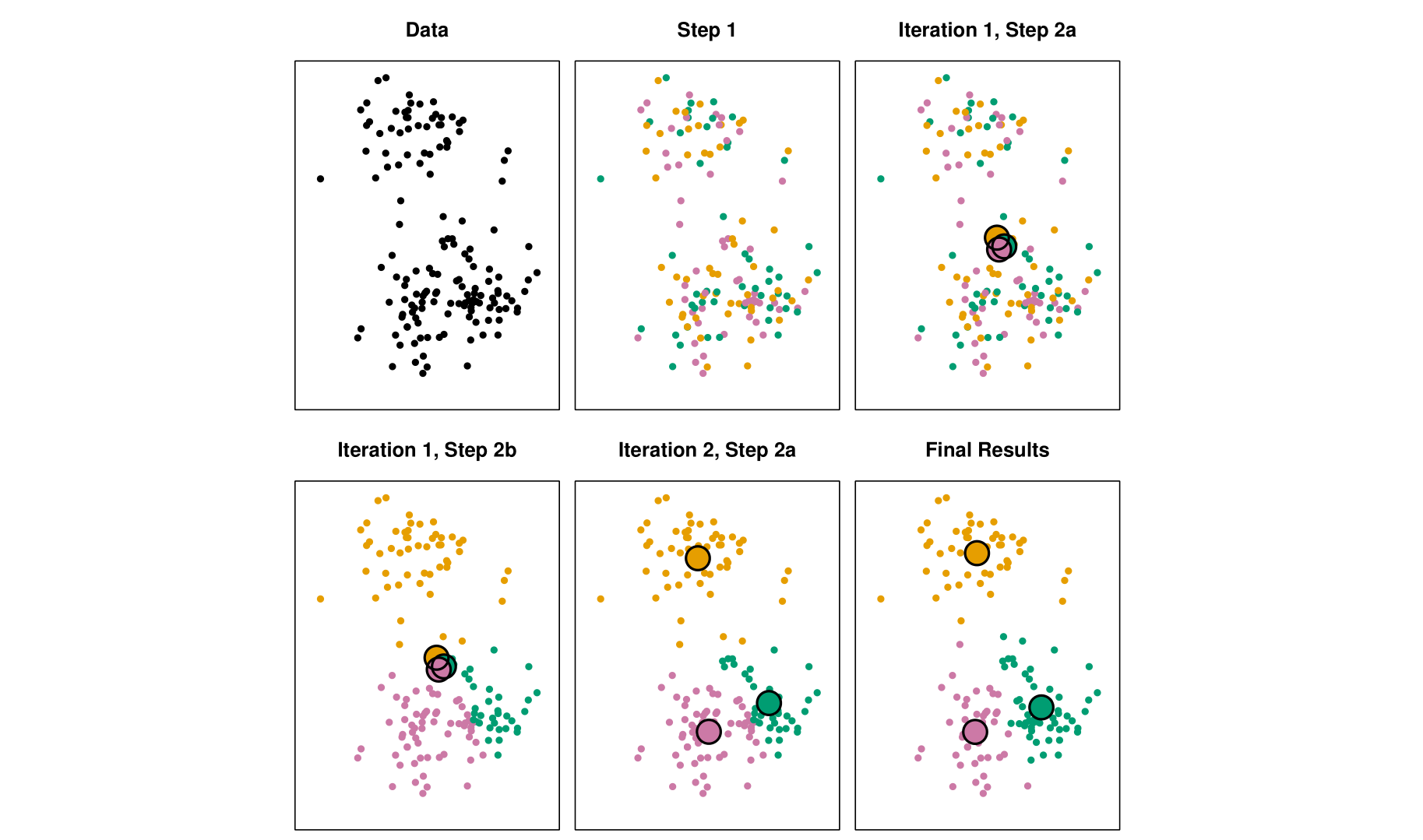
K-means Clustering은 분할 기반 clustering algorithm으로 data point를 iterative한 방식으로 K개의 cluster로 나누는 algorithm이다.

1. 정해진 K에 대해서, K개의 임의의 centroids를 설정
2. Cluster assignment가 수렴할 때까지 아래 과정을 반복
   1. 각 data point들을 가장 가까운(similar) centroid의 cluster 할당
   2. 각 cluster 내 data point들의 mean으로 centroid를 update

K-means clustering은 간단하고, 구현이 쉬우며, large dataset에 대해서도 효율적으로 동작하여 다른 clustering algorithm에 비해 비교적 빠르다는 장점이 있다.

하지만, 가장 큰 단점 중 하나인 cluster의 수 K를 사전에 지정해야 한다는 한계가 있으며, centroid의 초기 값에 따라 결과가 크게 달라질 수 있으므로 반복적 수행을 통해 최적의 clustering 결과를 empirical하게 찾아야 한다. 추가적으로 포함 관계를 갖는 data에 대한 clustering에는 적합하지 않고, outlier에 민감하다는 것도 단점으로 볼 수 있다.

Hierarchical Clustering

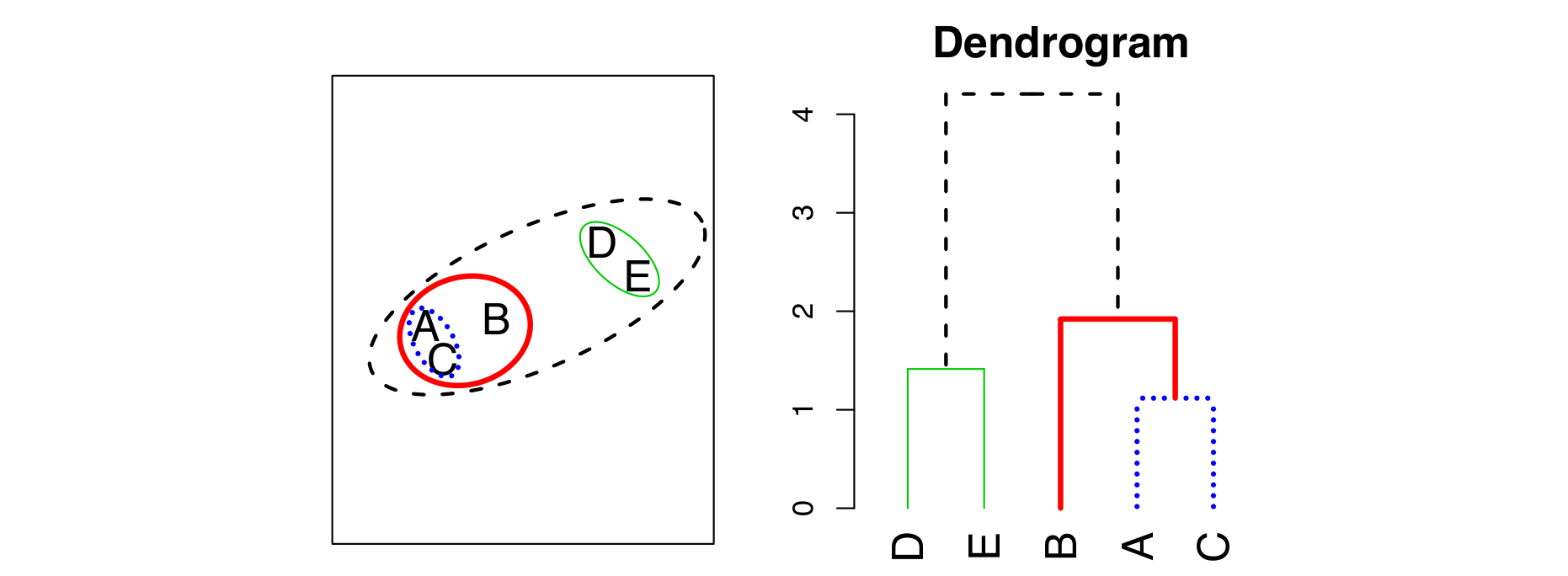
Hierarchical clustering은 dataset의 dendrogram을 만들어내는 tree-based clustering algorithm이다. 상향식(bottom-up, agglomerative) 또는 하향식(top-down, divisive) 접근법이 있으나, 여기서는 상향식 접근법을 소개한다.

1. 각 data point를 하나의 cluster로 간주
2. 오직 하나의 cluster만 남을 때까지 아래 과정을 반복
   1. 가장 가까운 두개의 cluster를 찾는다.
   2. 두개의 cluster를 합쳐 하나의 cluster로 만든다.
3. Dendrogram을 완성한다.

Hierarchical clustering은 K-means clustering과는 다르게 cluster의 수를 사전에 정할 필요가 없다는 장점이 있다. 또한, dendrogram을 통해 data의 hierarchical relationship을 쉽게 알 수 있다.

하지만, large dataset에 대해서 비효율적이고, outlier에 민감하다는 단점이 존재한다.

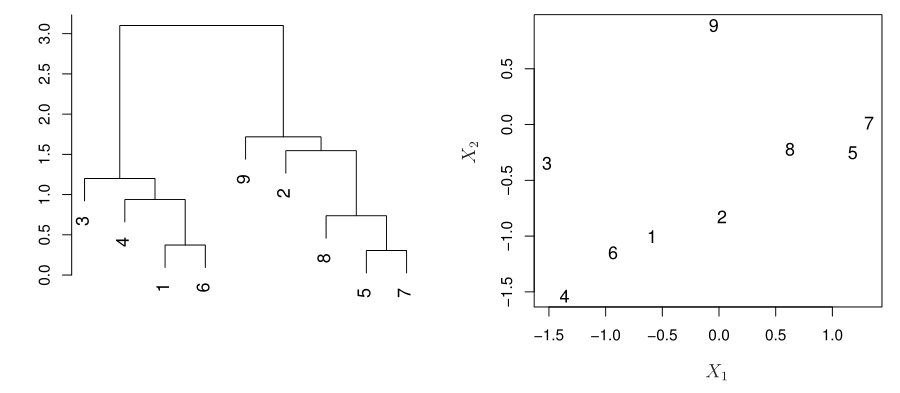
Hierarchical clustering으로 생성된 dendrogram을 해석할 때 주의해야 할 점은 어떤 두 data가 dendrogram에서의 높이차가 적다고하여 해당 data의 거리가 실제로 가까운 것은 아니라는 점이다.

위 예시 그림에서 9와 2는 하나의 level만 차이가 나지만, 실제 거리는 level 차이가 더 많이 나는 8, 5, 7보다도 멀다.

Distances in Clustering

Clustering에서의 핵심적인 요소 두 가지는 dimension reduction과 distance measure이다. Dimension reduction에 관해서는 앞서 설명한 바가 있으므로 (Dimension Reduction), 여기서는 clustering에서 사용되는 distance measure에 대해서 소개한다.

Inter-cluster Distance

Hierarchical clustering에서는 cluster 간의 거리를 어떻게 정하느냐가 중요한 hyperparameter이다.

Cluster간 거리를 정의하는 대표적인 linkage 방법은 다음과 같다.

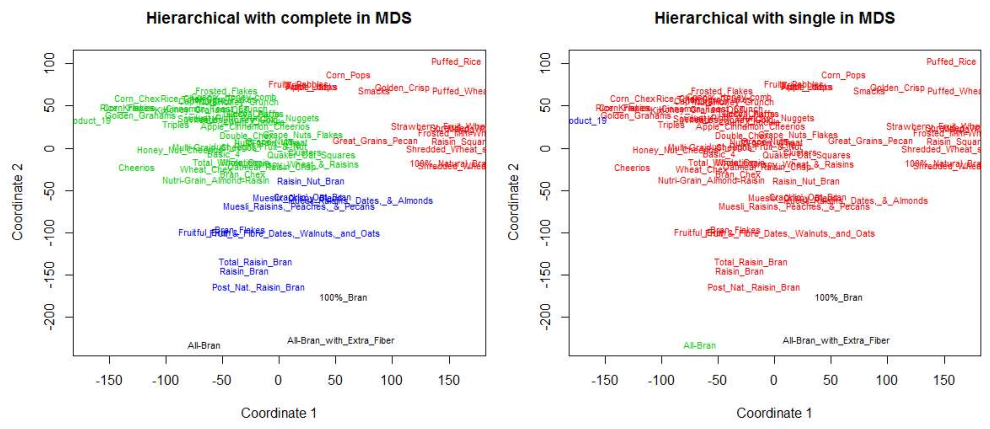
• Complete: 두 cluster A, B에 대해서 모든 pair의 distance 중 maximum 사용
  • 비교적 균일한 크기의 cluster들이 생성된다.
• Single: 두 cluster A, B에 대해서 모든 pair의 distance 중 minimum 사용
  • Chain effect로 인해 하나의 거대한 cluster가 생성될 가능성이 높다. 이를 통해 outlier를 잡아낼 수도 있다.
• Average: 두 cluster A, B에 대해서 모든 pair의 distance들의 mean 사용
  • Data가 많아질수록 계산량이 급증할 수 있기에 주의해야 한다.
• Centroid: 두 cluster A, B에 대해 각 cluster centroid들의 distance 사용
  • Data(특히 outlier)가 cluster로 병합되는 과정에서 centroid가 급격하게 바뀌어 data의 분포를 왜곡할 수도 있다.

Distance Measures

Clustering의 경우, 일반적으로 cluster 간의 차이는 클수록, 특히 cluster 내의 차이는 작을수록 좋은 clustering이라고 할 수 있다. 이 때, data point들 간의 차이를 정하는 distance measure를 어떤 것으로 사용하는 지가 (비단 clustering 뿐만 아니라) 최종적인 결과에 큰 영향을 미친다.

일반적으로는 data point들의 차이, 즉 dissimiliarity 또는 distance를 결정하는 metric으로는 Euclidean distance를 주로 사용한다.

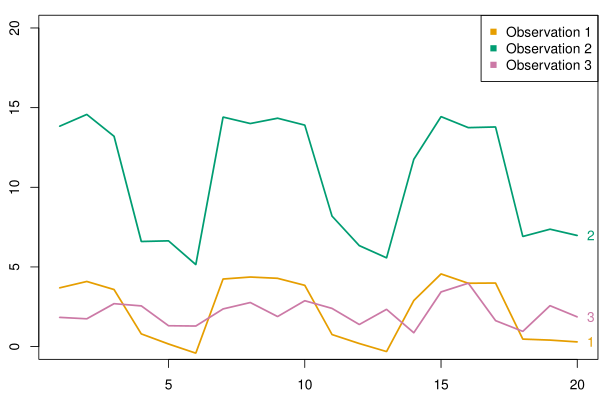
이와 더불어 correlation-based distance도 자주 사용되는 distance measure로써, data point들의 feature들의 correlation 정도로 similarity를 정하는 방법이다.

위 그림을 보면, Euclidian distance 기준으로는 observation 1 과 3이 더 가깝다고 볼 수 있으나, correlation-based distance 관점에서는 observation 1 과 2가 더 가깝다고 볼 수 있다.