Calculus Backgrounds

Matrix Derivatives

Types of Matrix Derivative

Type	Scalar $y$	Vector $\mathbf{y}$ $(m\times 1)$	Matrix $\mathbf{Y}$ $(m\times n)$
Scalar $x$	$\frac{\partial y}{\partial x}$	$\frac{\partial\mathbf{y}}{\partial x}$: $(m\times 1)$	$\frac{\partial \mathbf{Y}}{\partial x}$: $(m\times n)$
Vector $\mathbf{x}$ $(n\times 1)$	$\frac{\partial y}{\partial \mathbf{x}}$: $(1\times n)$	$\frac{\partial \mathbf{y}}{\partial \mathbf{x}}$: $(m\times n)$
Matrix $\mathbf{X}$ $(p\times q)$	$\frac{\partial y}{\partial \mathbf{X}}$: $(p\times q)$

Pay attention to the dimensions!

Gradient and Hessian

• $\nabla f(x)$ = the gradient of $f$
  • The transpose of the first derivatives of $f$.

\[\nabla f(x) := \begin{bmatrix} \frac{\partial f}{\partial x_1} \\ \vdots \\ \frac{\partial f}{\partial x_n} \end{bmatrix} = \left( \frac{\partial f}{\partial \mathbf{x}} \right)^T \in \mathbb{R}^{n\times 1}\]

• $\nabla^2 f(x)$ = the Hessian of $f$
  • The matrix of second partial derivatives of $f$.
  • The Hessian is a symmetric matrix.

\[\nabla^2 f(x) := \begin{bmatrix} \frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1 \partial x_2} & \dots & \frac{\partial^2 f}{\partial x_1 \partial x_n} \\ \frac{\partial^2 f}{\partial x_2 \partial x_1} & \frac{\partial^2 f}{\partial x_2^2} & \dots & \frac{\partial^2 f}{\partial x_2 \partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^2 f}{\partial x_n \partial x_1} & \frac{\partial^2 f}{\partial x_n \partial x_2} & \dots & \frac{\partial^2 f}{\partial x_n^2} \end{bmatrix} \in \mathbb{R}^{n\times n}\]

Jacobian and Matrix Derivative

• Jacobian when $\mathbf{x} \in \mathbb{R}^n, \mathbf{y} \in \mathbb{R}^m$

\[J := \frac{\partial \mathbf{y}}{\partial \mathbf{x}} = \begin{bmatrix} \frac{\partial y_1}{\partial x_1} & \frac{\partial y_1}{\partial x_2} & \dots & \frac{\partial y_1}{\partial x_n} \\ \frac{\partial y_2}{\partial x_1} & \frac{\partial y_2}{\partial x_2} & \dots & \frac{\partial y_2}{\partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial y_m}{\partial x_1} & \frac{\partial y_m}{\partial x_2} & \dots & \frac{\partial y_m}{\partial x_n} \end{bmatrix} \in \mathbb{R}^{m\times n}\]

• Matrix derivative when $\mathbf{X} \in \mathbb{R}^{p\times q}, \mathbf{Y} \in \mathbb{R}^{m \times n}, z \in \mathbb{R}$

\[\frac{\partial z}{\partial \mathbf{X}} = \begin{bmatrix} \frac{\partial z}{\partial x_{11}} & \frac{\partial z}{\partial x_{12}} & \dots & \frac{\partial z}{\partial x_{1q}} \\ \frac{\partial z}{\partial x_{21}} & \frac{\partial z}{\partial x_{22}} & \dots & \frac{\partial z}{\partial x_{2q}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial z}{\partial x_{p1}} & \frac{\partial z}{\partial x_{p2}} & \dots & \frac{\partial z}{\partial x_{pq}} \end{bmatrix}, \quad \frac{\partial \mathbf{Y}}{\partial z} = \begin{bmatrix} \frac{\partial y_{11}}{\partial z} & \frac{\partial y_{12}}{\partial z} & \dots & \frac{\partial y_{1n}}{\partial z} \\ \frac{\partial y_{21}}{\partial z} & \frac{\partial y_{22}}{\partial z} & \dots & \frac{\partial y_{2n}}{\partial z} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial y_{m1}}{\partial z} & \frac{\partial y_{m2}}{\partial z} & \dots & \frac{\partial y_{mn}}{\partial z} \end{bmatrix},\]

Useful Matrix Derivative

For $A \in \mathbb{R}^{n \times n}$,

• $\frac{\partial}{\partial x}(b^Tx) = \frac{\partial}{\partial x}(x^Tb) = b^T$

• $\frac{\partial}{\partial x}(x^Tx) = \frac{\partial |x|^2}{\partial x} = 2x^T$

• $\frac{\partial}{\partial x}(x^TAx) = x^T(A+A^T)$

  • $2x^TA$ if $A$ is symmetric.

Chain Rule

Chain Rule

Theorem: Chain Rule

When the vector $x$ is dependent on another vector $t$, the chain rule for the univariate function $f:\mathbb{R}^n \rightarrow \mathbb{R}$ can be extended as follows:

\[\frac{df({\mathbf{x}(t)})}{dt} =\frac{\partial f}{\partial x} \frac{d \mathbf{x}}{d t} = \nabla f(\mathbf{x}(t))^T \frac{d \mathbf{x}}{d t}.\]

• If $z=f(\mathbf{y})$ and $y=g(\mathbf{x})$ where $\mathbf{x}\in \mathbb{R}^n, \mathbf{y}\in \mathbb{R}^m, z\in \mathbb{R}$, then

\[\frac{d z}{d x_i} = \sum_j \frac{d z}{d y_j}\frac{d y_j}{d x_i} = \sum_j \frac{d y_j}{d x_i}\frac{d z}{d y_j}\]

(gradients from all possible paths)

• or in vector notation

\[\frac{d z}{d \mathbf{x}} = \frac{d z}{d \mathbf{y}} \frac{d \mathbf{y}}{d \mathbf{x}}\] \[[1\times n] \quad [1\times m] [m \times n]\]

It is the basis of the back propagation technique in neural nets.

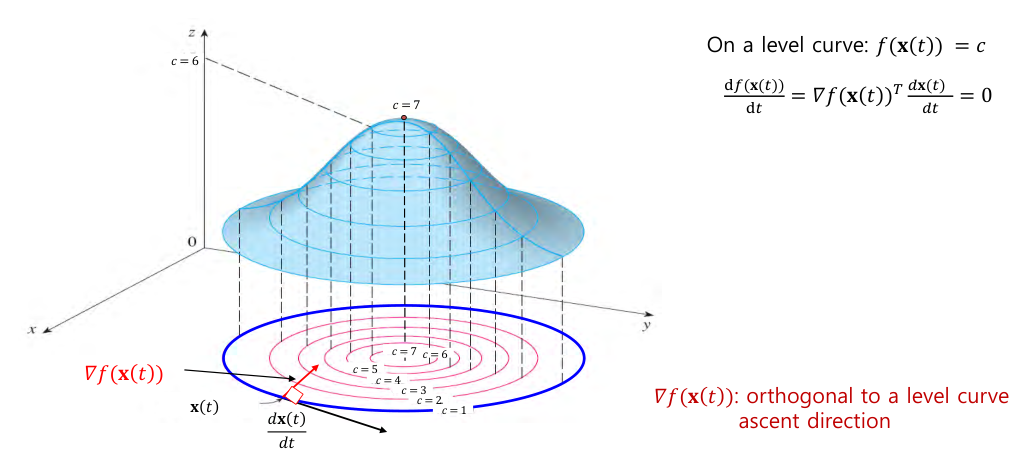
Chain Rule on Level Curve

• level curve : the set of $(x,y)$ such that $f(x,y)=c$.

• On level curve $f(\mathbf{x}(t)) = c$,

\[\frac{df({\mathbf{x}(t)})}{dt} = \nabla f({\mathbf{x}(t)})^T \frac{d\mathbf{x}(t)}{dt} = 0\]

In other words, $\nabla f({\mathbf{x}(t)})$ is orthogonal to the level curve and points to the ascent direction in which $f$ increases.

Directional Derivatives

• $f$ is continuously differentiable and $p \in \mathbb{R}^n$, directional derivative of $f$ in the direction of $p$ is given by

\[D(f(x);p) = \lim_{\varepsilon \rightarrow 0}\frac{f(x+\varepsilon p) - f(x)}{\varepsilon} = \nabla f(x)^Tp.\]

Taylor Series Expansion

• First order \(f(x+p) \approxeq f(x) + \nabla f(x)^Tp\)

• Second order \(f(x+p) \approxeq f(x) + \nabla f(x)^Tp + \frac{1}{2}p^T\nabla ^2 f(x)p\)

In general search (or leaning) algorithms, the first order expansion is sufficient.

Through the Taylor series expansion, it can be shown simply that $\nabla f(x)$ is the ascent direction.

\[\begin{aligned} f(x+\lambda \nabla f(x)) &\approxeq f(x) + \lambda\nabla f(x)^T\nabla f(x) \\ &= f(x) + \lambda \| \nabla f(x) \|^2\\ &\ge f(x) \end{aligned}\]