Bias-Variance Trade-off
Regression Function
두 variable Y, X가 있을 때, X를 사용해서 Y를 예측하는 model은 다음과 같이 쓸 수 있다.
\[Y=f(X)+\epsilon\]- Y: response, target
- X: feature, input, predictor
- $\epsilon$: errors
- $f$: regression function
이 때, 이상적인 $f(X)$는 어떻게 구할 수 있을까?
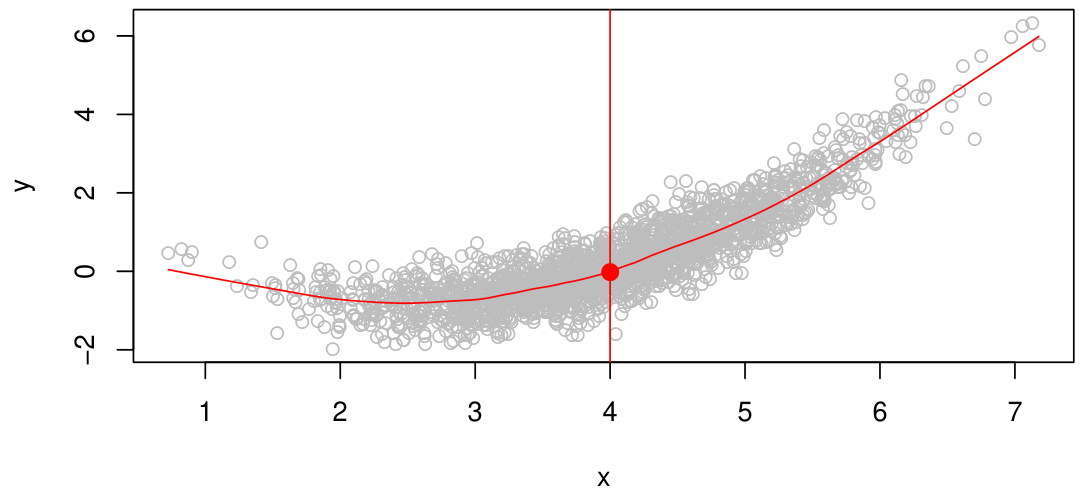
예를 들어, $X=4$ 일 때의 $Y$에 대한 예측은, $X=4$인 data의 $Y$ 값들의 평균으로 볼 수 있다. 즉, $f(4) = E(Y \mid X=4)$가 된다.
Function $f$의 모든 estimate $\hat{f}$에 대해, 다음이 성립한다.
\[E[(Y-\hat{f}(X))^2\mid X=x] = [f(x) - \hat{f}(x)]^2 + Var(\epsilon)\]여기서 $[f(x) - \hat{f}(x)]^2$은 reducible, $Var(\epsilon)$은 irreducible한 error에 관한 term이다.
만약 $\hat{f}(x)=E(Y\mid X=x)$이 되면, 이는 가능한 모든 $\hat{f}$ 중 $E[(Y-\hat{f}(X))^2\mid X=x]$를 minimize하는 estimate가 된다.
따라서, $f(x)=E(Y\mid X=x)$는 이상적인 regression function이 된다.
위 방법은 classification에 대해서도 동일하게 작동한다.
Nearest Neighbor Averaging
그러나 $E(Y\mid X=x)$를 알기 위해서는 $X=x$에 해당하는 data가 충분히 있어야 한다.
하지만, 일반적으로 모든 X값에 대한 data가 충분하지는 않다 (심지어 없을 수도 있다.)
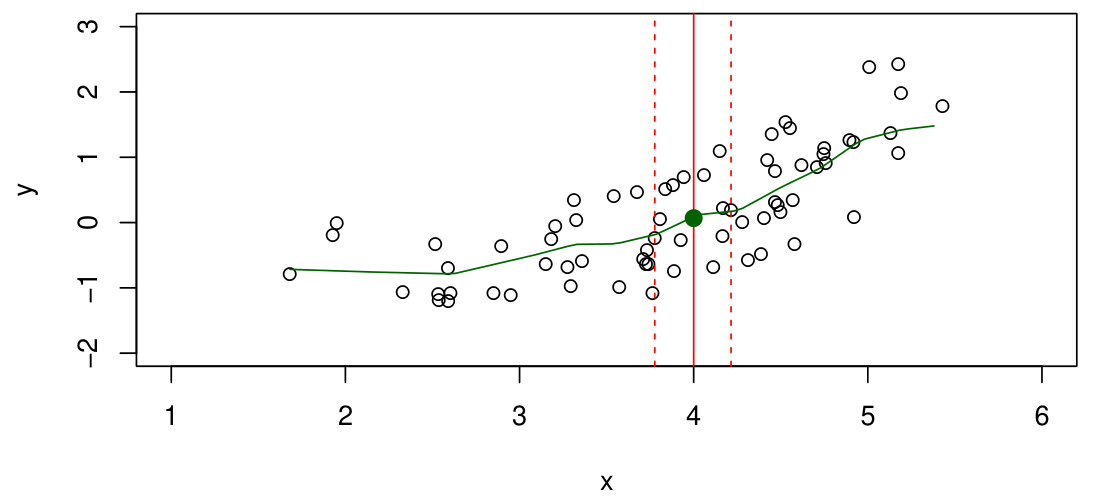
따라서, $E(Y\mid X=x)$를 다음과 같이 근사하여 계산한다.
\[\hat{f}(x) = Avg(Y\mid X\in N(x))\]이 때, $N(x)$는 $x$의 neighborhood이다.
그러나, 이러한 방법은 feature의 수 $p$가 커질수록 성능이 좋지 않다. 이를 curse of dimensionality라고 한다.
기본적으로 feature의 수, 즉 dimension이 증가하게 되면, data의 밀도가 sparse해지기에 특정 data point의 neighbor에 존재하는 data point의 수가 줄어든다. 즉 전체 data 수에 비해 Avg 계산에 사용되는 data의 비율이 줄어들기 때문에 성능이 줄어들게 되는 것이다.
위 방법은 classification에 대해서도 majority voting을 통해 동일하게 작동한다.
Parametric Model and Flexibility
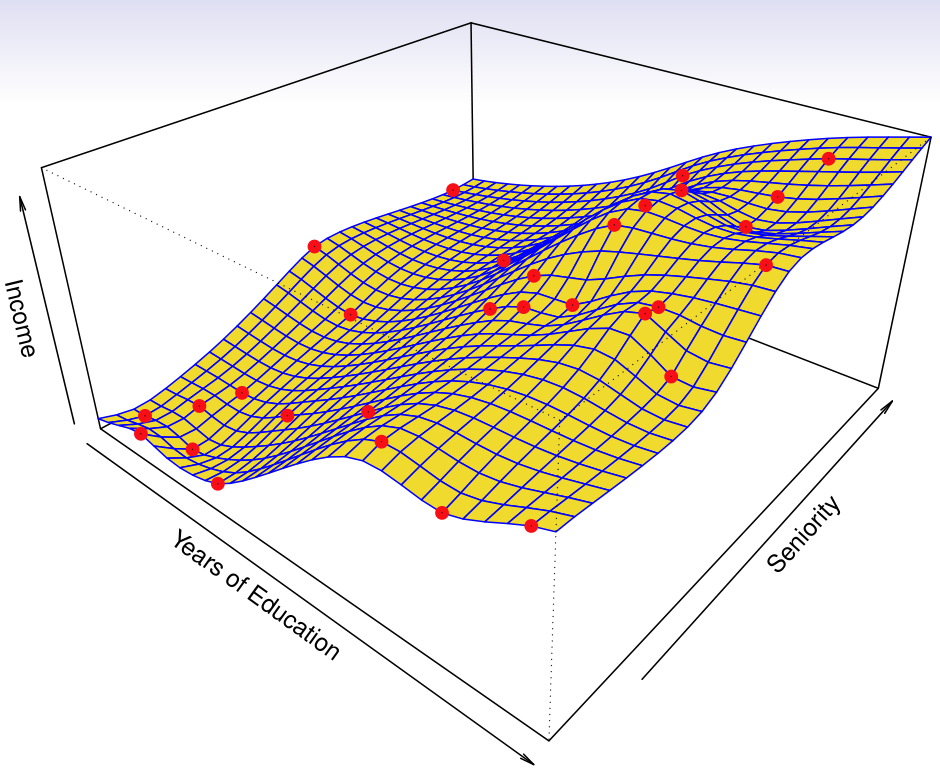
Regression function $f$를 다음과 같은 parameteric model로 생각해보자.
\[f(X) = \beta_0 + \beta_1X_1 + \dots + \beta_pX_p\]- Linear model
- Quadratic model
Model이 flexible해질수록, model의 accuracy가 올라가지만 complexity 역시 증가한다. Flexibility가 극단적으로 올라가면, model의 training data에 대한 error는 거의 0에 가깝게 줄어든다.
즉, 높은 flexibility는 필연적으로 overfitting을 유발한다.
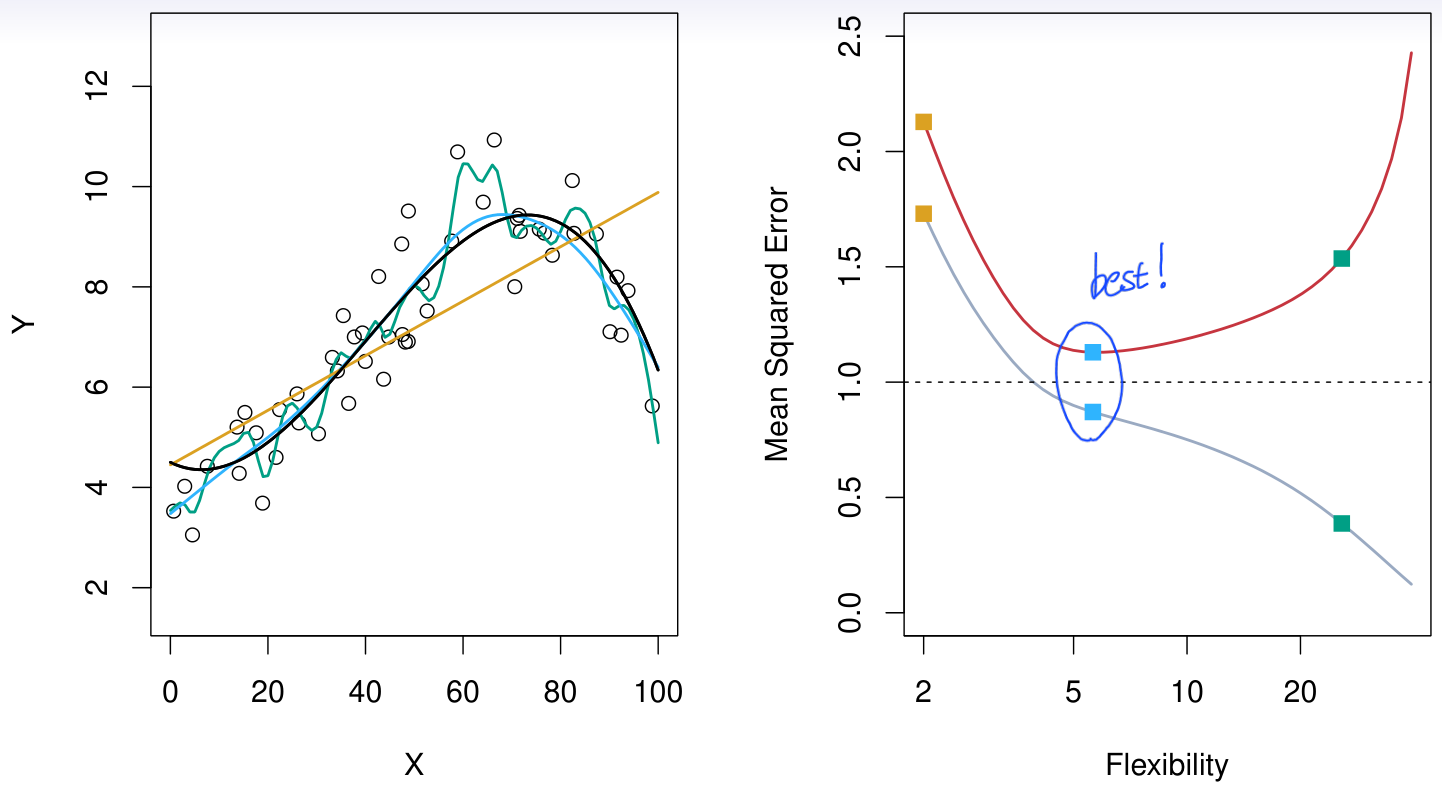
아래 그림으로부터 모델의 flexibility가 커질수록 training error(gray line)가 줄어드는 것을 볼 수 있으나, 어느 시점부터 test error(red line)이 증가하게 된다.
결국 좋은 model이란 (good fit model), training error가 아니라 test error를 최소화하는 model이다.
Model의 flexibility에 따른 trade-off를 정리하면 다음과 같다.
| Low Flexibility | High Flexibility |
|---|---|
| Interpretability | Accuracy |
| Underfit | Overfit |
| Parsimony (적은 수의 feature를 가지는 model) | Black-box (모든 feature를 포함하는 model) |
Flexibility for Several Cases
- Sample size가 크고, feature의 수가 작은 경우: flexible model 추천
- Sample size가 크면, flexiblity가 큰 model에 대해서도 feature 추정이 더 정확해진다. 또한 feature 수가 작기에 flexibility가 낮은 model은 data의 pattern을 잘 학습하지 못할 가능성이 높다.
- Sample size가 작고, feature의 수가 큰 경우: inflexible model 추천
- 이러한 경우의 문제는 overfitting 가능성이 높기에, model의 flexibility를 낮춰주는 것이 중요하다.
- feature와 response의 관계가 highly non-linear한 경우: flexible model 추천
- Flexibility가 높을 수록 data의 complex하고 non-linear한 관계를 잘 학습할 수 있다.
- The variance of the error terms, i.e., $\sigma^2 = Var(\epsilon)$인 경우: inflexible model 추천
- Error의 분산이 크다는 것은 data에 noise가 많다는 것을 의미한다. 이러한 경우, flexible model은 noise에 대해서도 data의 pattern으로 인식하고 학습을 진행하여 overfitting이 발생할 가능성이 높아진다.
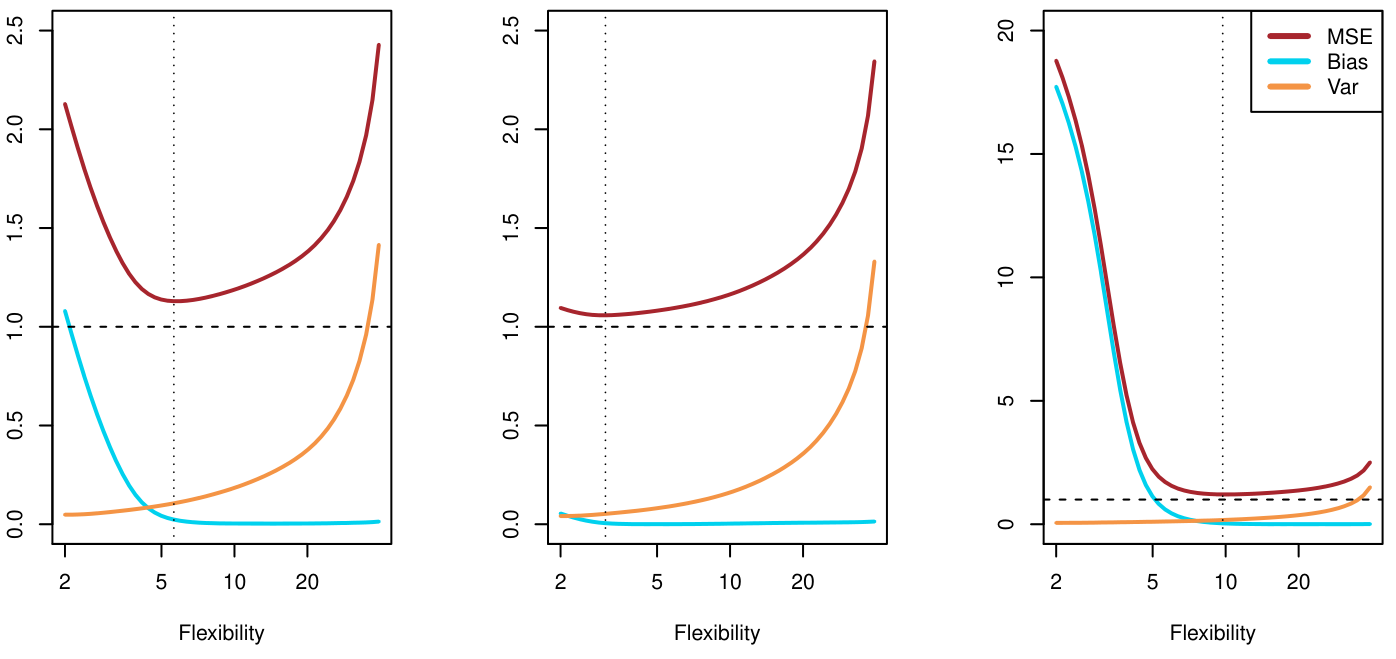
Bias-Variance Trade-off
Test data를 $(x_0,y_0)$이라고 하자. 이 때, $f$에 대해 아래 식이 성립한다.
\[E(y_0-f(x_0))^2 = Var(f(x_0)) + [Bias(f(x_0))]^2 + Var(\epsilon)\]여기서 $Bias(f(x_0))=E[f(x_0)]-f(x_0)$ 이다.
일반적으로, $f$의 flexibility가 올라가면, variance는 증가하고 bias는 감소하게 된다. 이러한 관계를 bias-variance trade-off 라고 말한다.