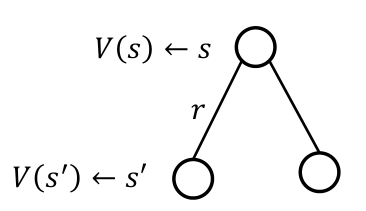Bellman Equation and Optimality
Bellman Equation for MRP
MRP $\langle S,P,R,\gamma \rangle$에서 value function $V(s_t)$에 대한 Bellman equation은 다음과 같이 정의된다.
\[\begin{aligned} V(s) &= E[G_t \mid s_t=s] \\ &= E[R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdots \mid s_t=s] \\ &= E[R_{t+1} + \gamma \sum_{k=0}^{\infty} \gamma^k R_{t+k+2} \mid s_t=s] \\ &= E[R_{t+1} + \gamma V(S_{t+1}) \mid s_t=s] \\ &= \sum_{s_{t+1}} p(s_{t+1} \mid s_t) [R(s_t, s_{t+1}) + \gamma V(s_{t+1})] \end{aligned}\]즉, 현재 state $s_t$에서의 value function은 미래 state $s_{t+1}$의 value function으로 표현할 수 있다 (one-step look ahead).
\[V(s) = R_s + \gamma \sum_{s'\in S} P_{ss'} V(s')\]Bellman Equation in a Matrix Form
\[V = R + \gamma PV\] \[\begin{bmatrix} V(s_1) \\ \vdots \\ V(s_n) \end{bmatrix} = \begin{bmatrix} R_1 \\ \vdots \\ R_n \end{bmatrix} + \gamma \begin{bmatrix} P_{11} & \cdots & P_{1n} \\ \vdots & \ddots & \vdots \\ P_{n1} & \cdots & P_{nn} \end{bmatrix} \begin{bmatrix} V(s_1) \\ \vdots \\ V(s_n) \end{bmatrix}\]위 식은 linear equation이므로, 다음과 같이 solution을 구할 수 있다.
\[V = (I-\gamma P)^{-1}R\]일반적으로 inverse matrix를 explicit하게 계산하는 경우, computation cost ($O(n^3)$ for $n$ states)가 너무 높으므로 DP와 같은 다른 방법을 사용한다.
Bellman Expectation Equation for MDP
위 방법과 유사하게, MDP에서 state-value function $V_\pi(s)$와 action-value function $Q_\pi(s,a)$에 대한 Bellman expectation equation을 다음과 같이 얻을 수 있다.
\[V_{\pi}(s) = E_{\pi} \left[ R_{t+1} + \gamma V_{\pi}(S_{t+1}) \mid S_{t} = s \right]\] \[Q_{\pi}(s, a) = E_{\pi} \left[ R_{t+1} + \gamma Q_{\pi}(S_{t+1}, A_{t+1}) \mid S_{t} = s, A_{t} = a \right]\]Bellman Equation for $V_{\pi}$ and $Q_{\pi}$
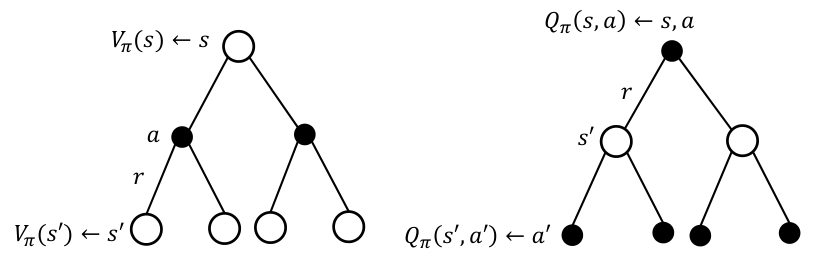
Bellman expectation equation을 $V_{\pi}$와 $Q_{\pi}$의 관계로써 나타낼 수 있다.
\[V_{\pi}(s) = \sum_{a \in \mathcal{A}} \pi(a \mid s) Q_{\pi}(s, a)\] \[Q_{\pi}(s, a) = R_{s}^{a} + \gamma \sum_{s' \in \mathcal{S}} P_{ss'}^{a} V_{\pi}(s')\]위 식을 이용하면, 아래와 같은 식을 얻는다.
\[V_{\pi}(s) = \sum_{a \in \mathcal{A}} \pi(a \mid s) \left( R_{s}^{a} + \gamma \sum_{s' \in \mathcal{S}} P_{ss'}^{a} V_{\pi}(s') \right)\] \[Q_{\pi}(s, a) = R_{s}^{a} + \gamma \sum_{s' \in \mathcal{S}} P_{ss'}^{a} \left( \sum_{a' \in \mathcal{A}} \pi(a' \mid s') Q_{\pi}(s', a') \right)\]Bellman Expectation Equation in a Matrix Form
\[V_{\pi} = R^{\pi} + \gamma P^{\pi} V_{\pi}\] \[\begin{bmatrix} V_{\pi}(s_1) \\ \vdots \\ V_{\pi}(s_n) \end{bmatrix} = \begin{bmatrix} R_1^{\pi} \\ \vdots \\ R_n^{\pi} \end{bmatrix} + \gamma \begin{bmatrix} P_{11}^{\pi} & \cdots & P_{1n}^{\pi} \\ \vdots & \ddots & \vdots \\ P_{n1}^{\pi} & \cdots & P_{nn}^{\pi} \end{bmatrix} \begin{bmatrix} V_{\pi}(s_1) \\ \vdots \\ V_{\pi}(s_n) \end{bmatrix}\]위 식 역시 다음과 같이 solution을 얻을 수 있다.
\[V_{\pi} = (I - \gamma P^{\pi})^{-1} R^{\pi}\]Bellman Optimality Equation
Optimal Value Function
Optimal state-value function $V_\ast(s)$는 모든 policy들을 고려했을 때, 가장 높은 state-value를 말한다.
\[V_\ast(s) = \max_\pi V_\pi(s)\]Optimal action-value function $Q_\ast(s,a)$ 역시 동일하게 정의된다.
\[Q_\ast(s,a) = \max_\pi Q_\pi(s,a)\]만약 모든 state $s \in S$에 대해, $V_{\pi_1}(s) \geq V_{\pi_2}(s)$인 경우, $\pi_1 \geq \pi_2$라고 표현하며, $\pi_1$이 $\pi_2$보다 더 나은 (better) policy라고 말한다.
만약 모든 policy에 대해 더 나은 policy $\pi_\ast$가 있다면, 이를 optimal policy라고 한다.
Theorem
- Optimal policy $\pi_\ast$는 항상 존재한다.
- Optimal policy $\pi_\ast$를 통해 계산된 state-value $V_{\pi_\ast}(s)$와 $Q_{\pi_\ast}(s,a)$는 각각 optimal state-value 및 action-value 이다. 즉, $V_{\pi_\ast}(s) = V_\ast(s)$, $Q_{\pi_\ast}(s,a) = Q_\ast(s,a)$.
Finding an Optimal Policy
만약 optimal action-value function $Q_\ast(s,a)$를 안다면, optimal policy를 다음과 같이 바로 얻을 수 있다.
\[\pi_{*}(a|s) = \begin{cases} 1 & \text{if } a = \arg\max\limits_{a \in A} Q_\ast(s, a) \\ 0 & \text{otherwise} \end{cases}\]즉, $Q_\ast(s,a)$가 가장 큰 action을 고르는 것이 optimal policy가 된다.
Bellman Optimality Equation for $V_\ast(s)$ and $Q_\ast(s,a)$
Bellman optimality equation은 $V_\ast(s)$와 $Q_\ast(s,a)$에 대한 iterative equation을 제시하며, 이를 풀어냄으로써 optimal value function 및 optimal policy를 얻을 수 있다.
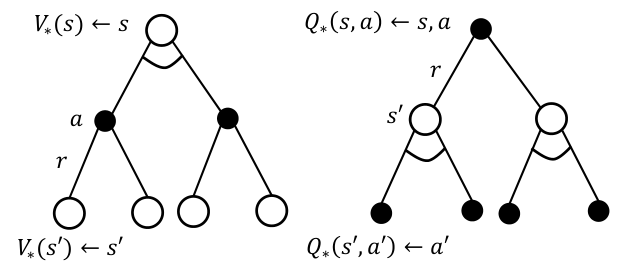
앞서 Bellman expectation equation과 마찬가지로 $V_\ast(s)$와 $Q_\ast(s,a)$ 관계를 다음과 같이 표현할 수 있다.
\[V_{\ast}(s) = \max_{a \in \mathcal{A}} Q_{\ast}(s, a)\] \[Q_{\ast}(s, a) = R_{s}^{a} + \gamma \sum_{s' \in \mathcal{S}} P_{ss'}^{a} V_{\ast}(s')\]위 식을 이용하면, 다음 Bellman optimality equation을 얻을 수 있다.
\[V_{\pi}(s) = \max_{a \in \mathcal{A}} \left( R_{s}^{a} + \gamma \sum_{s' \in \mathcal{S}} P_{ss'}^{a} V_{\ast}(s') \right)\] \[Q_{\pi}(s, a) = R_{s}^{a} + \gamma \sum_{s' \in \mathcal{S}} P_{ss'}^{a} \max_{a' \in \mathcal{A}} Q_{\ast}(s', a')\]Bellman optimality equation은 non-linear 하므로 단순한 matrix 연산으로 solution을 구할 수는 없다. 따라서, iterative alogirthm을 통해 solution을 구하게 된다. 자세한 방법에 대해서는 다음 post에서 다룰 예정이다.