Batch and Layer Normalizations
Internal Covariate Shift
Normalization은 데이터의 분포를 특정 범위나 특정 평균과 표준 편차로 조정하여 특정 feature에 대해 과대/과소 평가를 하지 않도록 만드는 과정을 말한다. 일반적으로 machine learning 등에서 input data에 대해 standard 또는 min-max normalization을 했던 이유이기도 하다.
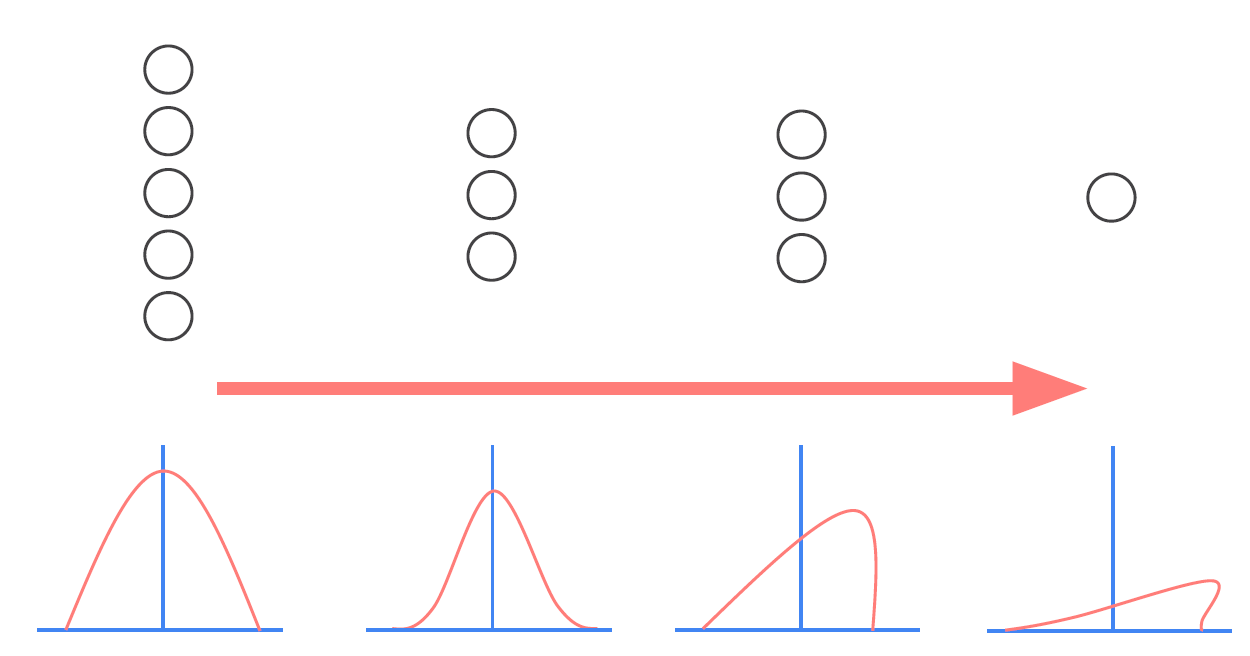
Deep learning에서도 input data에 대해서 똑같이 normalization을 할 수 있다. 하지만, 여러 layer를 갖는 neural net에서는 각 layer를 거칠 때마다 data의 분포가 계속적으로 변할 수 있다. NN에서는 각 layer의 input이 이전 layer의 output에 의존하기 때문에, 초기에 parameter가 지속적으로 바뀌는 과정에서 layer의 input의 분포가 일정하지 않게된다. 이를 internal covariate shift 현상이라고 한다.
Training data와 test data의 분포에 차이가 있는 경우를 covariate shift라고 한다.
Internal covariate shift 현상은 학습 속도를 느리게 만들고, parameter initialization에 따라 성능이 크게 달라지는 불안정성을 야기한다.
이러한 현상을 해결하기 위해 고안된 방법이 batch normalization이다.
Batch Normalization
Batch normalization은 각 mini-batch에 대해서 개별적으로 feature normalization을 하는 방법이다.
$n$-dimensional instance $x_i$로 구성된 mini-batch \(B=\{x_1,\dots,x_m\}\)가 있다고 하자.
이 때, Batch normalization은 다음과 같은 순서로 진행된다.
Mini-batch B의 feature별 평균과 분산 계산
\[\mu_B = \frac{1}{m} \sum_{i=1}^m x_i, \quad \sigma_B^2 = \frac{1}{m} \sum_{i=1}^m (x_i-\mu_B)^2\]- $\mu_B$와 $\sigma_B^2$는 $n$-dim vector가 된다.
Normalized mini-batch 계산
\[\hat{x}_i = \frac{x_i-\mu_B}{\sqrt{\sigma_B^2 + \epsilon}}\]- 여기서 $\epsilon$은 아주 작은 값 (대략 $10^{-5}$)으로, 0으로 나누어주는 것을 방지하는 값이다.
필요 시, 모델이 data range를 변경할 수 있도록 learnable parameter $\gamma$와 $\beta$를 이용해서 rescaling해준다.
\[y_i = \gamma\hat{x}_i + \beta\]- $\gamma$와 $\beta$로 인해 identity mapping이 가능해진다.
\(\{x_1,\dots,x_m\}\) 대신 \(\{y_1,\dots,y_m\}\)를 이용해 학습을 진행한다.
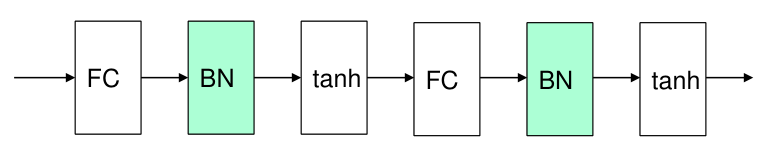
일반적으로 batch normalization layer는 fully connected layer를 거친 이후, activation function을 적용하기 전에 위치한다.
Test 과정에서는 training 과정에서 계산된 $\mu_B$와 $\sigma_B^2$를 running average로 계산한 값 $\mu_{avg}$와 $\sigma_{avg}^2$을 사용한다.
Batch normalization은 기본적으로 mini-batch의 statistics를 사용하기 때문에 너무 작은 크기의 mini-batch에 대해서는 제대로 적용되지 않을 수 있다.
또한, 가장 큰 단점으로는 RNN과 같은 sequential data의 경우에 input data size가 다르면 적용이 어렵다는 점이 있다.
일반적으로 sequential data의 mini-batch는 고정된 size를 정해두고, 그보다 짧은 data에 대해서는 나머지 공간에 대해 zero-padding을 적용하는데, 이러한 경우 batch normalization이 제대로 적용되지 않는 것은 자명하다.
이러한 이유로, sequential data를 사용하는 RNN, LSTM과 같은 모델에서는 batch normalization이 아닌 layer normalization 기법을 사용한다.
Layer Normalization
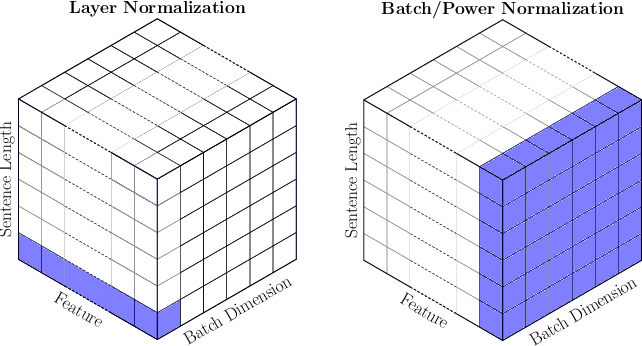
Layer normalization 역시 batch normalization과 유사하나, feature 단위가 아닌 sample 단위로 normalization을 진행한다는 차이점이 있다. 즉, mini-batch의 크기에 무관하고 sample들 간의 size가 달라도 normalization이 문제없이 수행된다.
$n$-dim sample $x_i$에 대해 layer normalization은 다음과 같은 순서로 진행된다.
Sample $x_i$의 평균과 분산 계산
\[\mu_i = \frac{1}{n} \sum_{j=1}^n x_i^j, \quad \sigma_i^2 = \frac{1}{n} \sum_{j=1}^n (x_i^j-\mu_i)^2\]Normalized sample 계산
\[\hat{x}_i^j = \frac{x_i^j-\mu_i}{\sqrt{\sigma_i^2 + \epsilon}}\]Learnable parameter $\gamma$와 $\beta$를 이용해서 rescaling
\[y_i^j = \gamma\hat{x}_i^j + \beta\]$x_i$ 대신 $y_i$를 이용해 학습을 진행
Layer normalization은 sample별로 normalization을 진행하기에 전체 dataset의 분포를 완전히 일정하게 만드는 것은 아니다.