Bagging and Random Forest

Ensemble

Ensemble 방법이란 하나의 target에 대해 여러개의 prediction model을 만든 후, 이를 결합하여 최종적인 prediction model을 만드는 방법을 통칭한다.

• 예: Bagging, Boosting, Random Forest

Ensemble 방법이 decision tree의 단점인 낮은 예측력과 결과의 불안정성을 해소한다는 것이 empirical하게 알려져있다 (Decision Trees).

Bagging

Bagging, 또는 bootstrap aggregation은 estimation의 variance를 줄이기 위한 방법론이다.

만약 우리가 n개의 training set을 따로 가지고 있고, 각각에 대한 학습 모델이 있다면, 그 모델들의 estimation의 variance는 1/n만큼 작아지게 된다. 이러한 효과를 동일하게 낼 수 있는 기법이 바로 bootstrap이다 (Bootstrap).

Bagging은 다음과 같이 동작한다.

1. B개의 bootstrap training data set ($Z^{\ast b}$)을 생성한다.
2. 각 $Z^{\ast b}$에 대해 prediction model $f^{\ast b}(x)$를 생성하고, estimation 값 $\hat{f}^{\ast b}(x)$을 계산한다.
3. 계산된 B개의 estimation 값의 평균을 통해 최종적인 estimation 값을 얻는다.
   • 만약 classfication model인 경우, B개의 estimation에 대한 majority voting을 통해서 최종 estimation을 결정한다.

\[\hat{f}_{bag}(x) = \frac{1}{B} \sum_{b=1}^B \hat{f}^{*b}(x)\]

Bagging with Decision Tree

Bagging의 원리는 decision tree와 같이 variance가 큰 model에 대해서 averaging을 통해 variance를 줄이는 것이다. 따라서, bagging의 baseline model은 variance가 크고 bias가 작은, 즉 overfitting된 model을 사용할 때 좋은 효과를 볼 수 있다.

이를 decision tree 관점에서 본다면, baseline model로 pruning을 하지 않은 fully-growing tree를 사용하는 것이 좋다.

Baseline model로 decision tree를 사용하는 경우 outlier에 둔감하다는 장점 또한 얻을 수 있다.

Bagging은 tree의 개수가 늘어난다고 하여 overfitting이 발생할 가능성이 커지지는 않는다. 일반적으로는 대략 100~200개의 tree를 사용한다.

다만, bootstrap data set에는 대략 60% 이상 겹치는 data가 존재하므로, tree간 의사결정이 크게 달라지지 않는다는 단점이 존재한다.

Random Forests

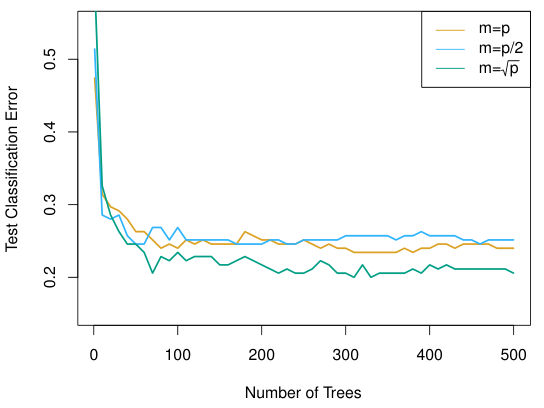
Random forests방법은 일반적인 bagging과 동일하나, random forests는 각 tree를 만들 때, feature를 모두 사용하지 않고, $m$개의 feature를 random하게 골라내어 tree를 만든다.

일반적으로 전체 feature가 $p$개일 때, $m$은 $\sqrt{p}$에 가까운 값을 사용한다.

간단한 idea이지만, 상당히 powerful한 성능 향상을 보여준다. 또한 tuning parameter가 전혀 없기 때문에 쉽게 사용할 수 있다는 장점이 있다.

Random forests는 일반적인 bagging 방법에 더 많은 randomness를 부여하여 예측력을 향상시키는 방법이다. 이를 통해 unstable unbiased model, 즉 variance가 크고 bias는 작은 model에 대해서는 randomness를 적절하게 부여한 ensemble 방법이 더욱 효과적임을 알 수 있다.