Backpropagation
우리는 앞서 FFN을 통해 input layer부터 output layer까지 순서대로 값을 계산하고 저장하는 작업을 수행했다. 이를 forward propagation이라고 한다.
이후, 이렇게 forward propagation을 통해 계산된 output과 미리 정의한 loss function으로 loss를 구하고, SGD 등의 학습 방법론을 이용하여 모델의 parameter를 학습하여야 한다. 이 과정은 결국 각 parameter에 대해 loss function에 대한 gradient를 계산을 요구하는데, 이 과정을 효율적으로 수행하는 방법론이 backpropagation이다.
Chain Rule of Calculus
If $z=f(\mathbf{y})$ and $y=g(\mathbf{x})$ where $\mathbf{x}\in \mathbb{R}^n, \mathbf{y}\in \mathbb{R}^m, z\in \mathbb{R}$, then
\[\frac{d z}{d x_i} = \sum_j \frac{d z}{d y_j}\frac{d y_j}{d x_i} = \sum_j \frac{d y_j}{d x_i}\frac{d z}{d y_j}\]Backpropagation
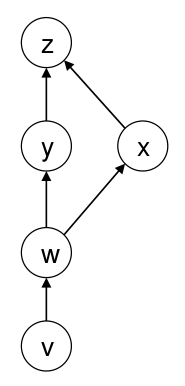
다음과 같은 chained function이 있다고 하자.
$x, y, w, v$를 학습하기 위해서는 $\frac{\partial z}{\partial x}, \frac{\partial z}{\partial y}, \frac{\partial z}{\partial w}, \frac{\partial z}{\partial v}$를 각각 구해야 한다.
이 때, backpropagation은 $z$와 가까운 변수에 대한 편미분 값을 구하고, 이를 다음 변수의 편미분 값을 구하는데 다시 사용한다 (memoization). 즉, 다음과 같은 순서로 계산한다.
$\frac{\partial z}{\partial y}$와 $\frac{\partial z}{\partial x}$을 계산한다.
1번에서 계산한 $\frac{\partial z}{\partial y}$와 $\frac{\partial z}{\partial x}$을 이용하여 $\frac{\partial z}{\partial w} \leftarrow \frac{\partial y}{\partial w}\frac{\partial z}{\partial y} + \frac{\partial x}{\partial w}\frac{\partial z}{\partial x}$를 계산한다.
2번에서 계산한 $\frac{\partial z}{\partial w}$을 이용하여 $\frac{\partial z}{\partial v} \leftarrow \frac{\partial w}{\partial v}\frac{\partial z}{\partial w}$를 계산한다.
Backpropagation은 dynamic programming을 사용하기에 속도가 무척 빠르다.
Backpropagation at FFN
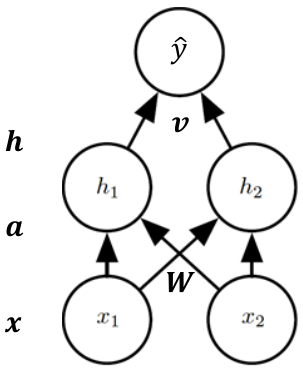
추가 예시로, hidden layer 1개를 갖는 FFN 모델에 대해 backpropagation이 어떻게 진행되는지 확인해보자.
우선, forward propagation은 다음과 같은 순서로 진행된다.
$a \leftarrow Wx$
$h \leftarrow \sigma(a)$
$\hat{y} \leftarrow v^T h$
$J \leftarrow (\hat{y} - y)^2 + \lambda ( \vert W \vert_F^2 + \vert v \vert_2^2)$
이후, backpropagation은 다음과 같은 순서로 진행된다.
$g \leftarrow \nabla_{\hat{y}} J = 2 (\hat{y} - y)$
$\nabla_v J \leftarrow \nabla_v [(\hat{y} - y)^2 + \lambda (\vert W \vert_F^2 + \vert v \vert_2^2)] = gh + 2 \lambda v$
$g \leftarrow \nabla_h J = \nabla_h [(\hat{y} - y)^2 + \lambda (\vert W \vert_F^2 + \vert v \vert_2^2)] = gv$
$g \leftarrow \nabla_a J = g \odot \sigma’(a) \quad \text{(elementwise)}$
$\nabla_W J \leftarrow \nabla_W [(\hat{y} - y)^2 + \lambda (\vert W \vert_F^2 + \vert v \vert_2^2)] = gx^T + 2 \lambda W$
위 loss function에서 $\lambda$ term은 regularization term이다.