Autoencoder
Autoencoder
Autoencoder (AE)란 input과 output이 동일하도록 학습하는 neural network를 의미한다. 언뜻보면 아무런 의미가 없는 NN으로 보이지만, 주로 데이터의 dimension reduction 및 feature extraction을 위해 사용되는 모델이다.
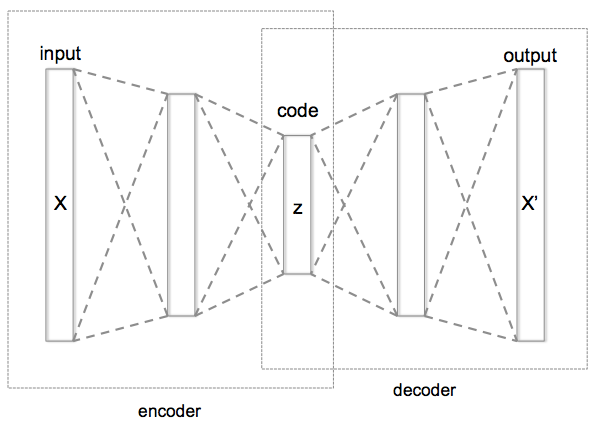
기본적인 구조는 input 데이터를 encoding하는 encoder와 encoding된 vector를 다시 decoding하는 decoder로 나뉜다. 이 때, encoding을 거친 hidden vector를 code 또는 feature라고 한다. 이러한 code들의 space를 latent space라고 한다.
Code가 input data보다 더 작은 dimension을 가지는 경우, undercomplete AE라고 한다. 일반적인 AE는 이를 의미한다.
아래는 AE의 기본 구조를 나타내는데, AE의 목적은 input X와 output X’이 같도록 학습하는 것이다.
Dimensionality Reduction
일반적으로 dimensionality reduction은 주로 PCA를 이용했으나 (참고: Dimension Reduction in ML), AE를 이용하면 더 powerful한 nonlinear dimensionality reduction이 가능해진다.
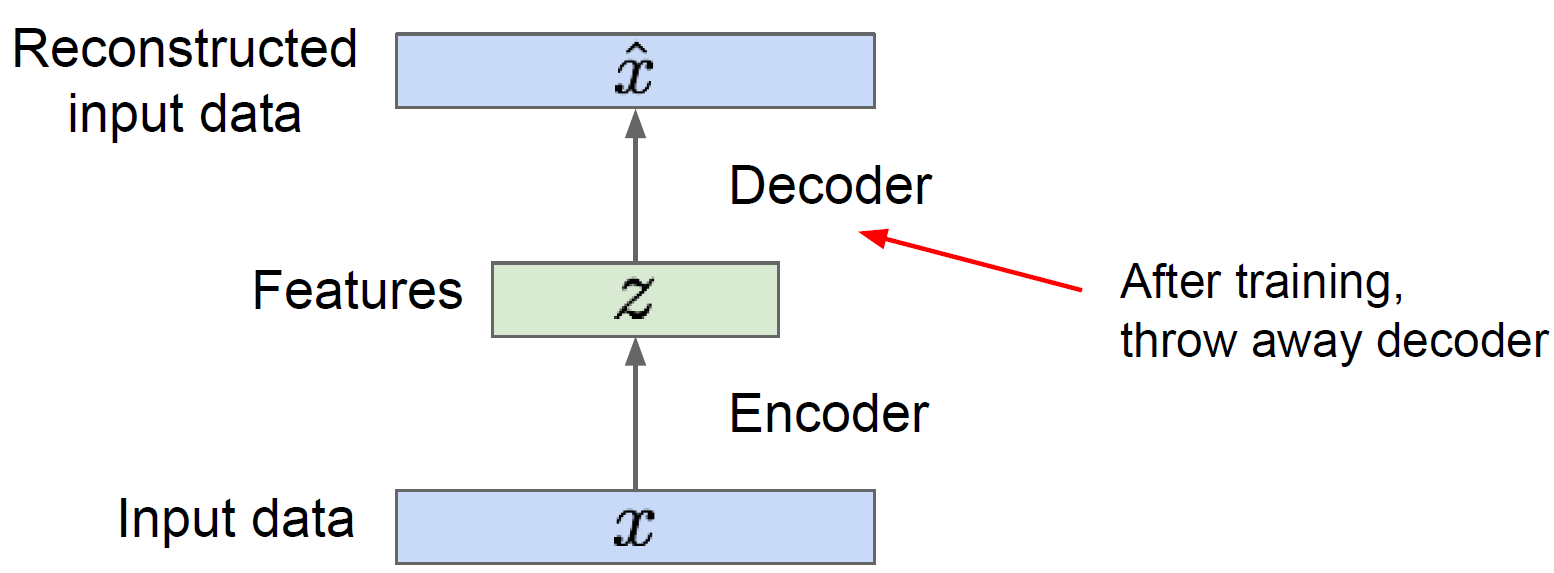
AE를 이용한 dimensionality reduction은 학습을 마친 AE에서 decoder를 떼버리고, encoder만을 사용하면 된다. 즉, code를 reduction된 input으로 사용된다.
AE for Pretraining
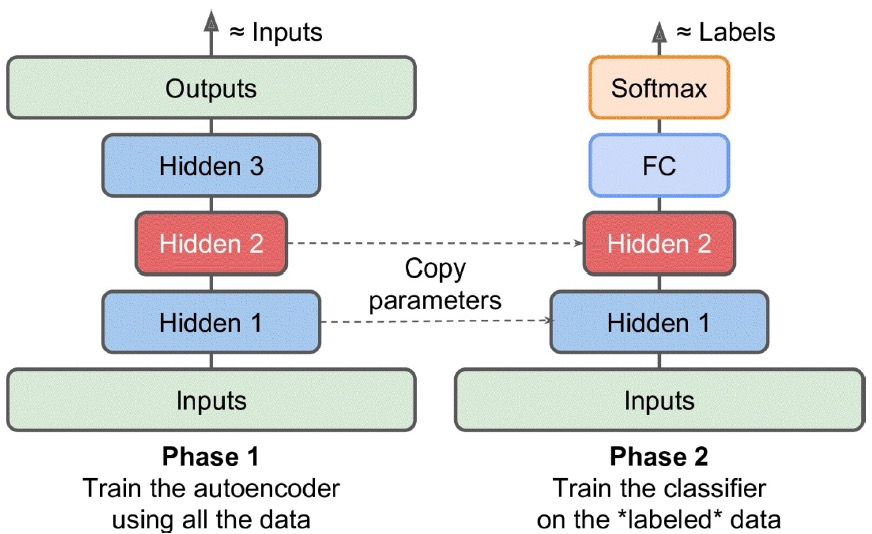
AE를 pretrained model로써 사용할 수도 있다. 이는 특히, 일부 data에만 label이 존재하는 semi-supervised learning에 효과적이다.
AE를 pretrained model로 사용하기 위해서는 우선 AE에 대해서 학습을 마친 후, decoder를 제거한다. 즉, dimensionality reduction과 마찬가지로 encoder만을 사용한다.
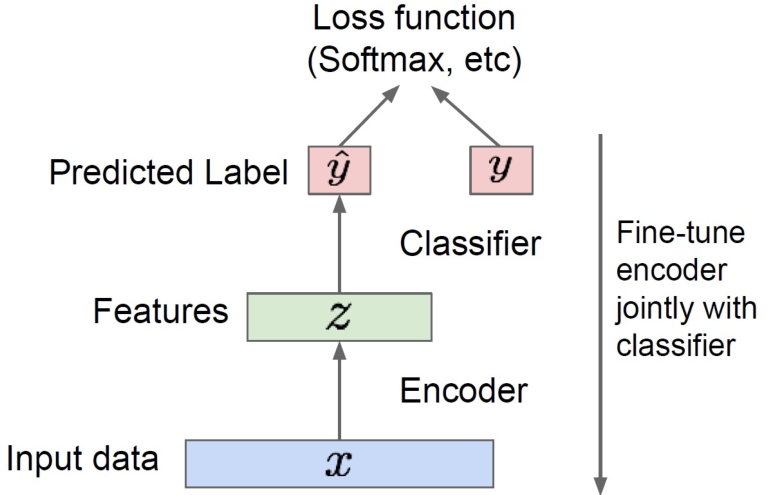
Encoder 모델은 결국 feature를 뽑는 것으로도 볼 수 있으므로, AE의 hidden layer 위에 특정 작업을 위한 layer를 새롭게 올리고 fine-tuning을 진행한다.
Semi-supervised learning의 경우, label이 없는 데이터를 pretraining에 사용하고, label이 있는 데이터를 fine-tuning에 사용한다.
Variations of AE
Regularized AE
Regualrized AE는 code에 대한 penalty term을 loss function에 추가하여 학습하는 방식이다. 이를 통해 code에 대한 dimension 제약을 따로 두지 않아도, 보다 중요한 feature만 뽑아낼 수 있다.
만약 $f$: encoder, $g$: decoder라고 한다면, regularized AE는 다음과 같은 loss function을 갖는다.
\[L(x, g(f(x))) + \Omega(h) = L(x, g(f(x))) + \lambda \sum_i \vert h_i \vert\]일반적으로 unique하고 important한 feature를 얻기 위해서 sparsity를 증가시키는 lasso regularization을 사용한다.
Deep AE
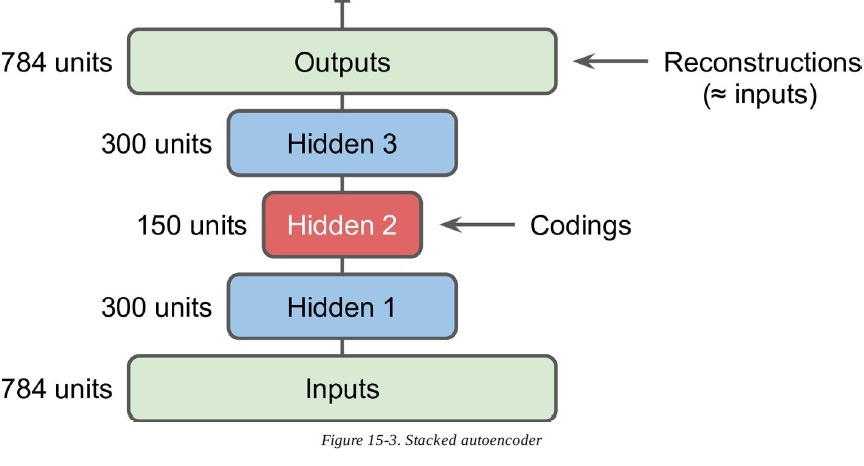
일반적인 AE는 하나의 encoder layer와 하나의 decoder layer로 구현된다. 물론 AE가 이렇게 동작해야한다는 제약은 따로 없기에, hidden layer를 추가하여 model을 더 deep하게 만들 수 있다. 이는 computational cost를 증가시키지만, 복잡한 data에 대해서 더 좋은 성능을 보여준다.
Deep AE의 경우, 처음부터 fully training하기 보다는 shallow AE 모델을 training하고, train된 모델에 layer를 추가하여 다시 학습하는 greedy supervised pretraining 방법을 주로 사용한다.
Deep AE는 일반적으로 symmetrical architecture를 갖는다. 즉 coding을 중심으로 대칭인 layer들로 구성한다.
Deep AE 역시 uncomplete AE와 마찬가지로 encoder만을 사용해 pretraining modelf로 사용할 수 있다.
Denoising AE
AE의 loss function 자체를 변경하여 원하는 효과를 얻는 새로운 NN으로 만들 수 있다.
일반적으로 AE의 경우 input과 output의 차이를 최소화하도록 loss function을 설정한다. 즉, loss function은 $L(x, g(f(x)))$이 된다.
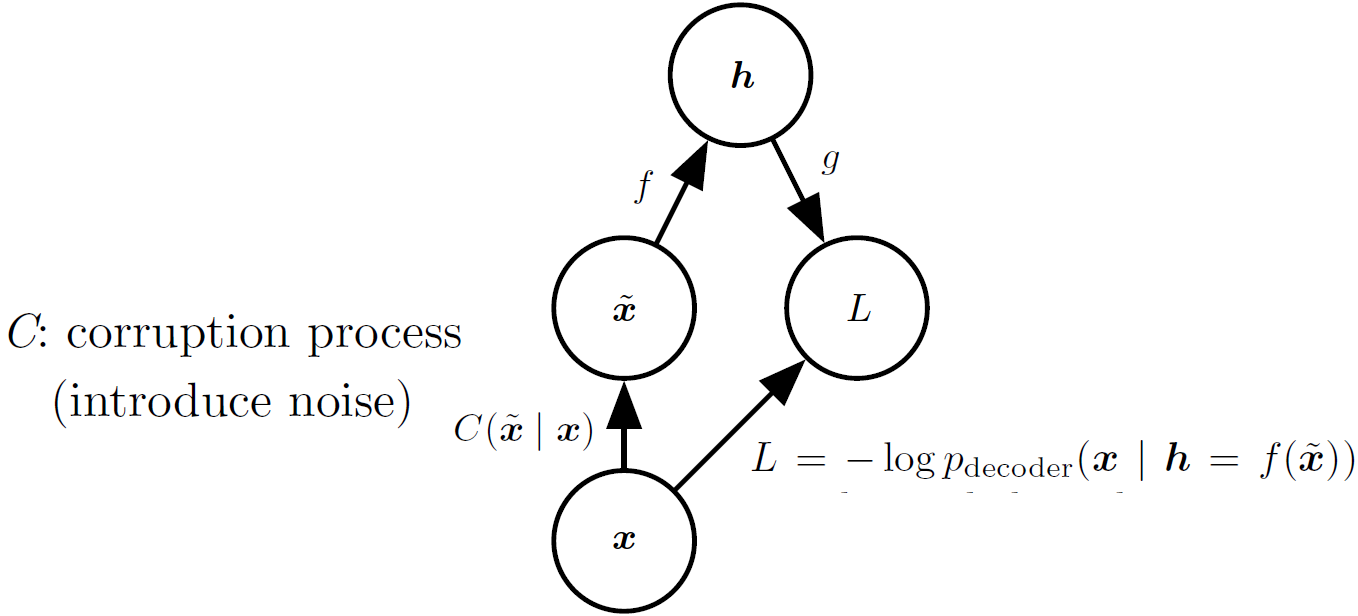
Denoising AE는 input $x$에 약간의 noise를 추가한 $\tilde{x}=x+\epsilon$을 forward하여 얻은 $g(f(\tilde{x}))$와 본래의 input $x$의 차이를 최소화한다. 즉, loss function은 $L(x, g(f(\tilde{x})))$이 된다.
Contractive AE
Contractive AE는 regularized AE의 일종으로 penalty term이 $h$에 대한 함수에서 $x$와 $h$를 모두 고려한 함수로 바꾼 것으로 다음과 같다.
\[L(x, g(f(x))) + \Omega(h,x) = L(x, g(f(x))) + \lambda \sum_i \Vert \nabla_x h_i \Vert^2\]이러한 penalty term은 모델이 x가 살짝 바뀌어도 h가 크게 바뀌지 않도록 학습하도록 만든다.
Contractive AE는 모델의 robustness를 강화했다는 점에서 denoising AE와 유사한 모델이다. 하지만, denoising AE는 reconstruction을 통해서 이를 강화했다면, contractive AE는 encoder를 통해서 이를 강화했다는 점에서 차이가 있다. 이러한 차이로 인해, encoder만 사용하는 model에서는 contractive AE가 더 유용하다.
하지만, Contractive AE는 매번 gradient 계산이 필요하다는 점에서 다른 AE에 비해 높은 computation cost를 요구하기에 training이 쉽지 않다는 단점이 있다.