Affine Transformation and Correction
Affine Transformation and Correction
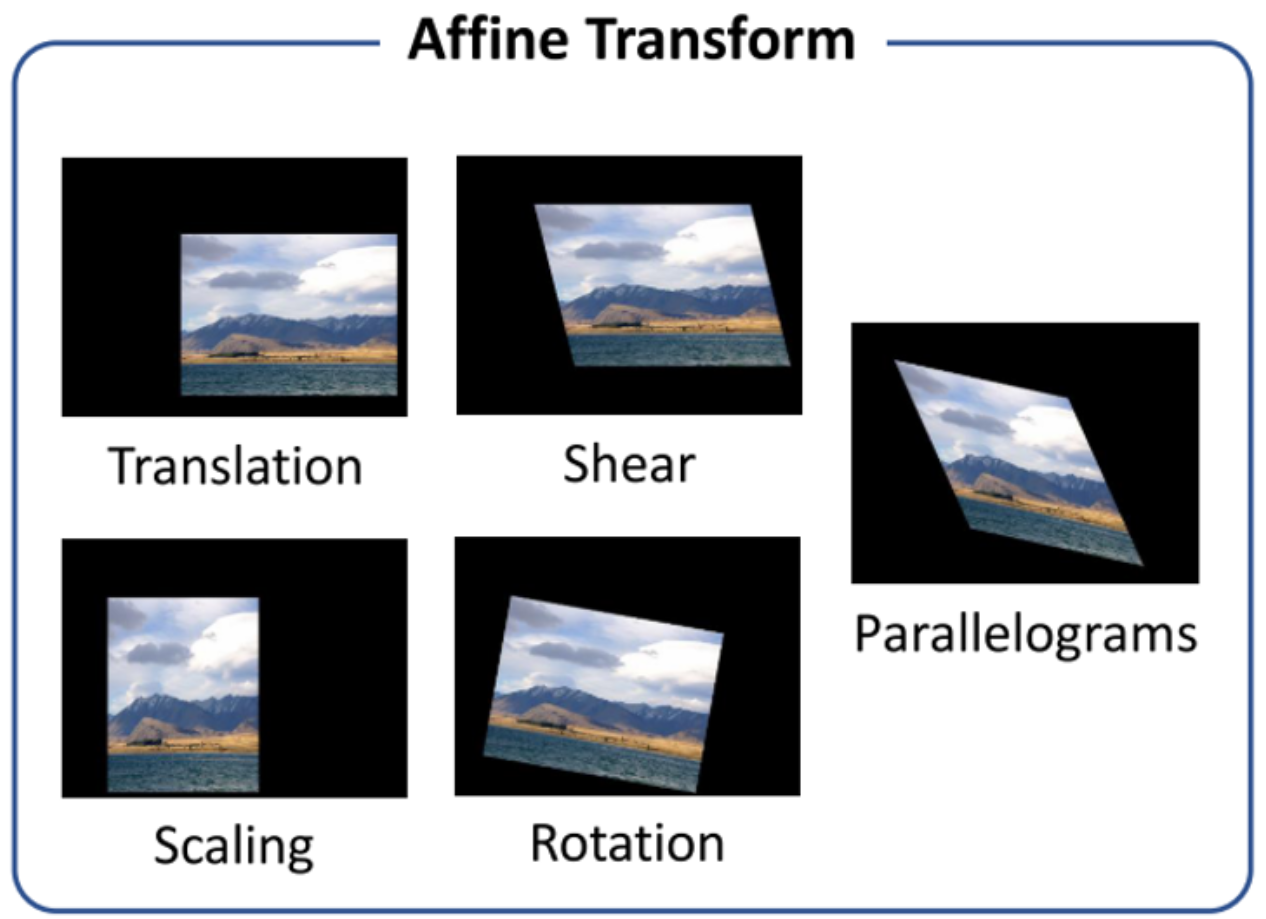
Affine Transformation
아래 형태의 변환을 affine transformation이라고 한다.
\[\begin{bmatrix} x^{1} \\ y^{1} \end{bmatrix} = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} + \begin{bmatrix} e \\ p \end{bmatrix}\]- Shift
- Scale
- Flip
- Rotation
- Shear
- Inverse Transformation
Interpolation
Affine Transformation 시, edge 부분의 pixel에 대한 interpolation이 필요하다.
- Neareast Neighbor: 가까운 1개의 pixel을 사용 (Zero-order Hold와 유사)
- Bilinear: 가까운 4개의 pixel을 사용하고 거리비에 따라 계산
- Bicubic: 가까운 16개의 pixel을 사용하고 거리비에 따라 계산
Correction
Gamma Correction
모든 display device는 image의 밝기를 다르게 표현하며, 이는 주로 $\gamma$로 표현된다: $F(D)=D^\gamma$.
따라서, 만약 display device의 $\gamma$를 안다면, 최종 pixel 값에 $\gamma$의 inverse를 제곱해주면 실제 밝기의 image로 출력된다: $(D^{1/\gamma})^\gamma=D$. 이를 gamma correction이라고 한다.
Histogram Equalization
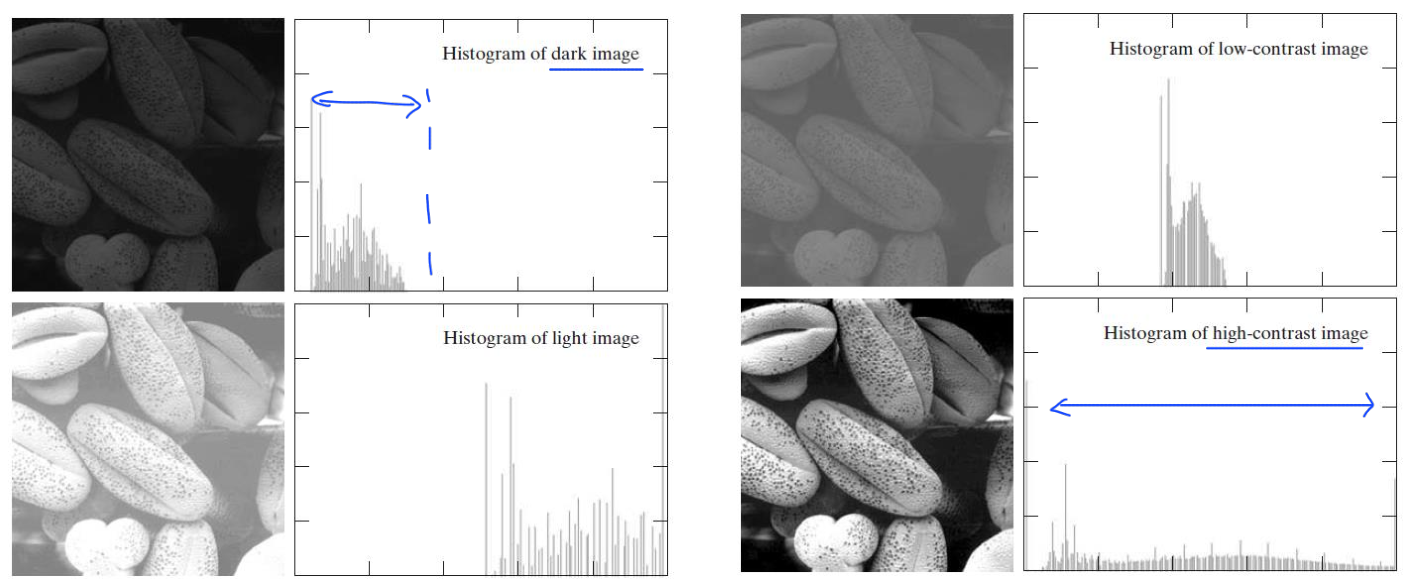
x축(수평축)은 밝기 값, y축(수직축)은 밝기 값에 대응되는 크기를 가진 픽셀 수로 하여, image를 histogram으로 표현할 수 있다.
- 히스토그램이 고르게 분포할수록 명암 차이가 크다. (high-contrast)
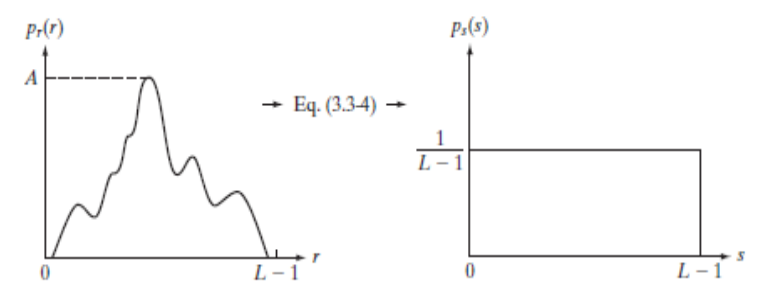
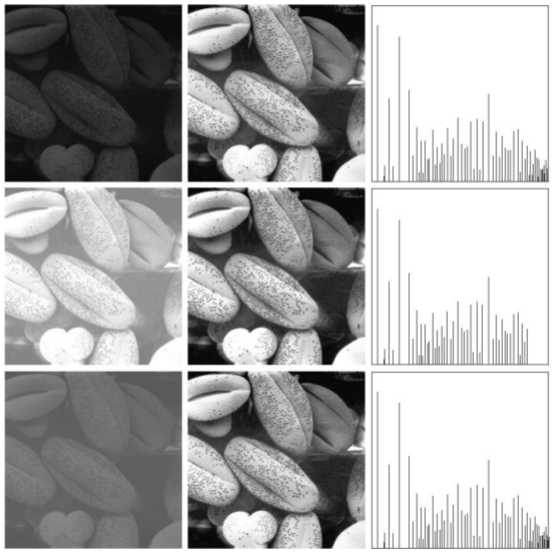
Histogram equalization이란, histogram의 분포를 평평하게 만들어 image를 보다 선명하게 만들어주는 기법이다.
This post is licensed under CC BY 4.0 by the author.